| Magische vierkanten |  |
Magische vierkanten zijn tabellen van 3 bij 3, 4 bij 4, .... velden waarin oplopende getallen 1,2,3,...
zodanig zijn geplaatst dat de som van elke rij, kolom en diagonaal gelijk is.
Hieronder staan twee voorbeelden:
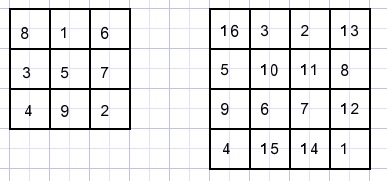
Hoeveel bedraagt die som bij een n x n vierkant?
Bekend is : 1 + 2 + 3 + ... + n = n(n+1)/2.
Voor een n*n vierkant is de som van alle velden 1 + 2 + 3 + ...+ n2 = n2(1+n2)/2
De som van een rij, kolom of diagonal is deze som gedeeld door n.
Zo'n som is dus n(1 + n2)/2.
Magische vierkanten spreken al eeuwenlang tot de verbeelding.
Het rechter 4 x 4 vierkant hierboven is te zien op de gravure "Melencolia" dat Dürer in het jaar 1514 maakte.
Merk op dat in het midden van de onderste rij 1514 staat.

Hoe maak je een magisch vierkant?
Eerst het linker, 3 x 3.
We zouden zo gauw geen goede aanpak weten.
Een wiskundige doet dan een stap terug en probeert eerst een eenvoudiger geval.
Alleen de eis dat de som van de rijen, kolommen en diagonalen gelijk is.
Daaraan voldoet een vierkant met alleen de cijfers 1......1 Beetje flauw, dat wel.
Een volgende stap is een vierkant waarin alleen per kolom, rij of diagonaal verschillende cijfers staan
waarvan dus de som steeds gelijk is.
We nemen de cijfers 0,1,2 de som is dan steeds 3.
Hier staat zo'n vierkant:
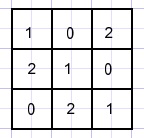
Het probleem is dat een cijfer in het vierkant meerdere malen vorkomt.
Dat is te verhelpen met een truc.
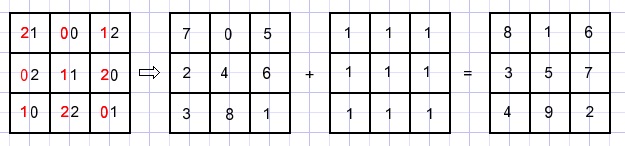
We spiegelen het vierkant om de middelste kolom en voegen dan de twee vierkanten samen:
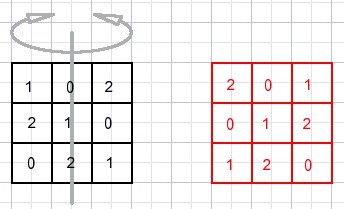
Nu is de som steeds 33, alle getallen zijn verschillend maar de volgorde 1,2,3... klopt niet.
Of toch wel?
Beschouw het getal als geschreven in het 3-tallig stelsel, dus vermenigvuldig het linker cijfer van een
veld met 3 en tel daar het rechter cijfer bij op.
Dat geeft de cijfers 0,1,2,3,4,5,6,7,8. Bijna goed.
We tellen nu 1 op bij elk veld en ziedaar.
Eigenlijk tellen we het eerste flauwe voorbeeld 1,1,....1 op.
Een andere benadering
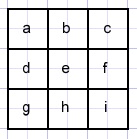
We gaan uit van een leeg 3 x 3 vierkant.
De velden (links naar rechts, boven naar onder) noemen we a,b,c,d,e,f,g,h,i cijfers die we nog niet weten.
Nu is een stelsel vergelijkingen op te stellen
 |
a + b + c = 15 d + e + f = 15 g + h + i = 15 a + d + g = 15 b + e + h = 15 c + f + i = 15 a + e + i = 15 c + e + g = 15 |
Dit stelsel is niet oplosbaar omdat er 9 variabelen zijn en maar 8 vergelijkingen.
Wel zien we dat e = 5, het middelste veld kan niet anders dan de waarde 5 hebben.
Laten we eens a =1 maken.
Dat levert naast weer e = 5 de voorwaarde op: f + h = 2.
Dat kan niet want dan zou f = h = 1 zijn.
De 1 moet dus aan de rand in het middelste veld staan. Neem b = 1, dus h = 9.
Nu resteert voor a en c de cijfers 6 en 8. Neem a = 8.
Daaruit volgen de andere cijfers.
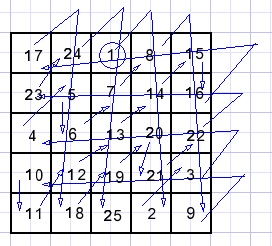
Snelle methode om n * n vierkanten te maken als n oneven is
Begin midden boven met het cijfer 1.
Ga voor het volgende cijfer 1 veld diagonaal rechts naar boven maar
- als dit veld bezet is, ga dan naar het veld onder het laatst ingevulde
- als het veld rechts naast het vierkant ligt, ga dan 3 velden naar links (n voor n*n)
- als het veld boven het vierkant ligt, ga dan 3 velden omlaag (n voor n*n)
Hieronder staat hoe met deze methode een 5*5 magisch vierkant ontstaat: