Eindexamen meetkunde 3 jarige H.B.S. in 1926 Hieronder staat het eindexamen meetkunde van de 3 jarige H.B.S. te Amsterdam van het jaar 1926. Er waren nog geen rekenmachines en ook geen gradenbogen. De leerlingen moesten het doen met potlood, passer en liniaal. Tijdsduur bedraagt 2 uur, voor vier vraagstukken. De antwoorden en uitwerkingen zijn van mijzelf. 1. Twee cirkels met stralen R en r raken elkaar uitwendig. De afstand tussen de raakpunten van de gemeenschappelijke uitwendige raaklijn is a. 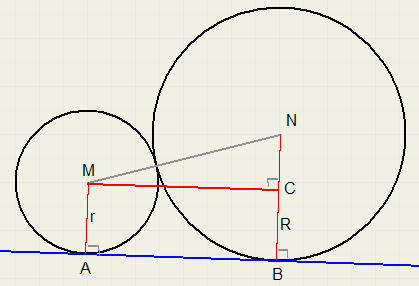Bewijs, dat a = 2  \ R r In de figuur hierboven is AB = MC = a MA = r NB = R NC = R - r ..............................{ABCM is een rechthoek} MN = R + r Opmerking: MN staat loodrecht op de raaklijn door het raakpunt van beide cirkels. (raaklijn is niet getekend) MN is dus een rechte lijn. Toepassing van de stelling van Pythagoras in DMCN: (R + r)2 = a2 + (R-r)2 R2 + 2Rr + r2 = a2 + R2 - 2Rr + r2 a2 = 4Rr a = 2  \ R r 2. Van een regelmatige achthoek is de zijde z. a. Bereken de oppervlakte van die achthoek. b. Construeer een vierkant, dat een even grote oppervlakte heeft als die achthoek. De achthoek ABCDEFGH hierboven is getekend binnen het vierkant WXYZ. 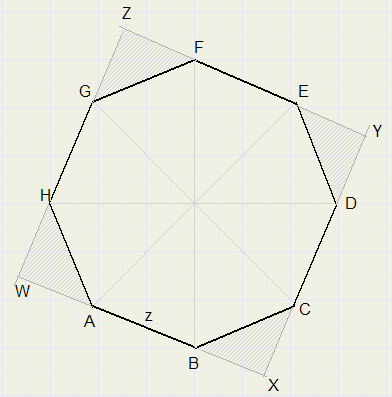De oppervlakte van de achthoek is gelijk aan de oppervlakte van het vierkant minus de gearceerde hoekpunten. a. Uit de symmetrie van de figuur volgt dat LCBX = LBCX = 45 graden. Pythagoras in DBXC 2BX2= z2 BX2 = z2 / 2 ....................BX = 1 2  z  \ 2 oppervlakte DBXC = z2 / 4 Alle gearceerde driehoeken hebben dus samen oppervlakte z2 WX = XY = z + z  \ 2 Oppervlakte ABCDEFGH = oppervlakte WXYZ - z2 = 2 æ z + z  \ 2 ö è ø - z2 = 2 z 2  \ 2  + 2 z 2 b. De stelling van Pythagoras is op te vatten als optelling van de oppervlakte van vierkanten waarvan de zijden even lang zijn als de zijden van een rechthoekige driehoek. 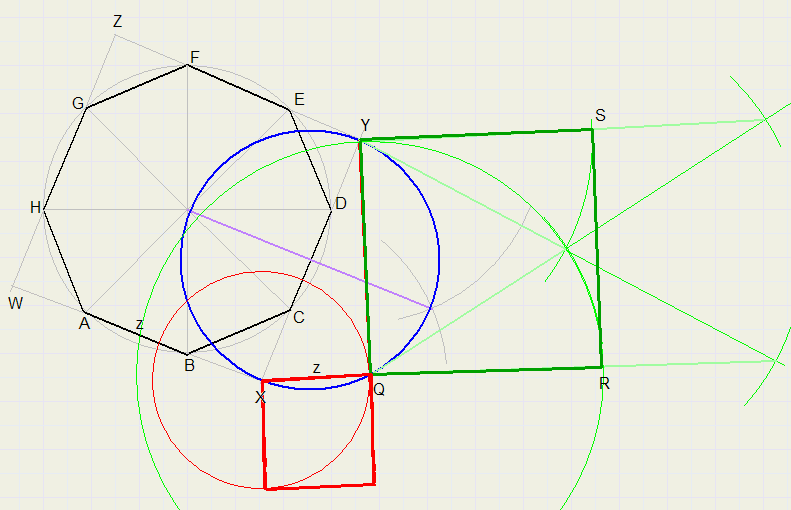Beschouw XY als de schuine zijde van een rechthoekige driehoek. Beschouw XY ook als middellijn van een cirkel. Construeer het midden van XY en teken de cirkel. (blauw) Cirkel lengte z om vanuit X (rood). Q is het snijpunt van de twee cirkels. Trek QX en QY. Construeer vierkant QRSY (groen). QRSY heeft dezelfde oppervlakte als ABCDEFGH. DXQY is rechthoekig omdat LQ op de middellijn staat van een cirkel. Voor een meer gedetailleerde beschrijving van meetkundige constructies met passer en liniaal kijk [ hier ] 3. Van een cirkel is een koorde \ 2 en de pijl van het bijbehorende segment 1 −  1 2   \ 2 a. bereken de straal van die cirkel b. bereken de oppervlakte van het segment De straal van de cirkel is even r genoemd. 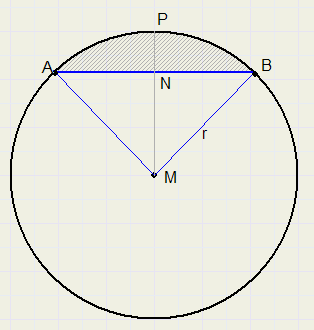Een koorde is een lijnstuk waarvan het begin- en het eindpunt op dezelfde cirkel liggen. Het bijbehorende segment is de gearceerde oppervlakte. Met de pijl van het segment wordt bedoeld het lijnstukje NP. a. AB = \ 2 ......zodat.........NB = 1 2   \ 2 PM = r...........zodat ...................MN = r −  æ 1 −  1 2   \ 2 ö ­ ­ è ø Pas nu Pythagoras toe in DMBN 2 æ r −  æ 1 −  1 2   \ 2 ö ­ ­ è ø ö ­ ­ è ø  +  2 æ 1 2   \ 2 ö ­ ­ è ø  = r 2 r 2 − 2 r  æ 1 −  1 2   \ 2 ö ­ ­ è ø  +  2 æ 1 −  1 2   \ 2 ö ­ ­ è ø  +  1 2  = r 2 −2 r  æ 1 −  1 2   \ 2 ö ­ ­ è ø  + 1 −  \ 2  +  1 2  +  1 2  = 0 −2 r  æ 1 −  1 2   \ 2 ö ­ ­ è ø  + 2  æ 1 −  1 2   \ 2 ö ­ ­ è ø  = 0 −2 r + 2 = 0 r = 1 b. Wegens BN = MN = 1 2   \ 2 ..........geldt......LBMN = LNBM = 45 graden. Uit de symmetrie volgt dat LAMB = 90 graden. De oppervlakte van sector ABM van de cirkel is dus p/4 De oppervlakte van DABM = 1/2..............zodat het segment ABP een oppervlakte heeft van p/4 - 1/2 4. 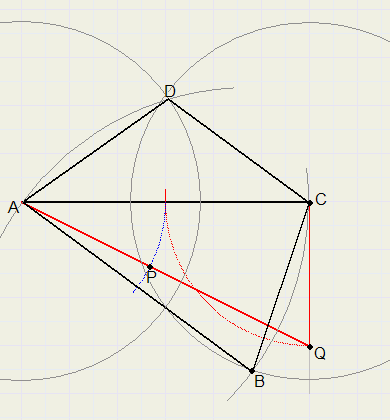Van een gelijkbenig trapezium is de langste der evenwijdige zijden gelijk aan de diagonaal, de kortste der evenwijdige zijden gelijk aan een been. Construeer dit trapezium, als de diagonaal gegeven is. 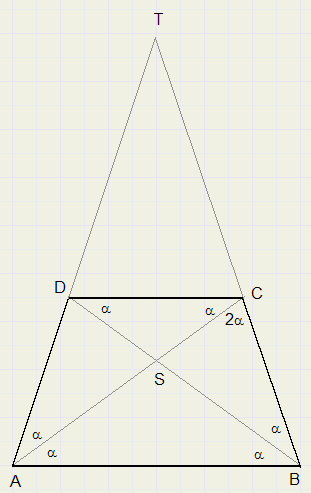Eerst eens een kladplaatje tekenen van een mogelijk trapezium Een voorgevoel zegt ons, dat het handig kan zijn de benen door te trekken naar de top T, zodat het trapezium onderdeel wordt van een gelijkbenige driehoek. In de figuur hierboven geldt dus: AD = DC AC = AB Stel nu, dat LCAB = a.....dan is LDCA = a..........{wegens AB en CD evenwijdig} LDAC = a..........{wegens AD = DC} LCBA = 2a...........{wegens gelijkbenigheid trapezium} LACB = 2a...........{wegens AC = AB} In DABC geldt dus..........5a = 180, zodat a = 36 graden. En ook LT = 36 graden Wegens LTAC = LATC geldt...........AC = CT Bij gegeven lengte van AC moet dus een hoek van 36 graden worden geconstrueerd waarover AC moet draaien. Of we construeren de lengte van been BC. Stel, dat AB = AC = 1 .........{we voeren even een eigen lengtemaat in} Stel AD = DC = x Omdat AC deellijn is in DABT geldt.........{deellijnstelling} AB : AT = BC : CT............zodat 1 : (1 + x) = x : 1 x2 + x - 1 = 0 ............{ABC formule}........ x = − 1 2  +  1 2   \ 5 We beginnen de constructie, uitgaande van AC - construeer het midden M van AC - construeer een loodlijn op AC in punt C, CQ = CM - trek lijn AQ - cirkel AM om vanuit A, AP = AM PQ is de lengte van een been van het trapezium, immers AC = 1 CQ = 1 2 AQ = 1 2   \ 5 PQ = − 1 2  +  1 2   \ 5 Cirkel AC om vanuit A en cirkel lengte PQ om vanuit C, het snijpunt is B van het trapezium. Cirkel ook AB om vanuit B en PQ vanuit A, het snijpunt is punt D van het trapezium.