

| meetkunde / gonio puzzel (28) |  |
Deze puzzle werd aangetroffen in de Faceboek groep "geometria":
(geplaatst door Eldeniz Hesenov)
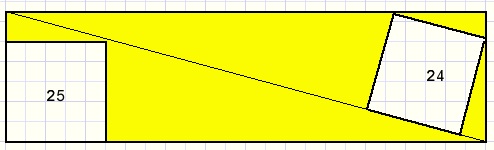
We zien een rechthoek met daarin twee vierkantjes met oppervlakten 25 en 24.
Gevraagd: de grootte van de geel gekleurde oppervlakte.
De aanpak
Voor de hand ligt de oppervlakte van de gehele rechthoek te bereken en daar die van de vierkantjes weervanaf te halen.
Door de hele figuur zien we rechthoekige driehoekjes die gelijkvormig zijn.
Bij bekende hoeken zijn de zijden van de rechthoek te berekenen.
Het is handiger een hoek als onbekende te nemen inplaats van de zijden van de rechthoek,
want dat laatste levert een stelsel van twee vergelijkingen op.
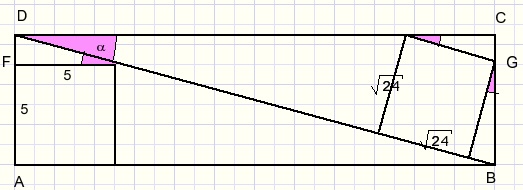
We stellen de onbekende hoek α
Dan is AD te berekenen uit het gegeven AF=5.
BC is te berekenen uitgaande van een zijde van het driehoekje met oppervlakte 24.
Nu hebben we twee formules met α en daaruit is α op te lossen door gelijkstelling.
Immers: AD = BC.
Oplossing

Ziehier de vergelijking waaruit α moet worden opgelost.
Omdat mij dit niet meteen lukte heb ik eerst de grafische oplossing gekozen.
Met Graphics-Explorer twee vergelijkingen invoeren:
-
formule 1: y = 1 + tan(x)
formule 2: y = sqrt(24/25)*(sin(x) + 1/cos(x))
Nu inzoomen op het snijpunt van de lijnen en we zien: x = 15.
Onbekend is dan of dit precies is of een benadering.
De vergelijking
Eerst eens alles uitschrijven in sin en cos, noemers gelijk maken:
De cos(α) noemers vallen nu tegen elkaar weg.
Nu plegen we een slimme substitutie: sin(α)+cos(α)=y
Dat levert een kwadratische vergelijking in y op.
Hieronder het bewijs dat die substitutie correct is:
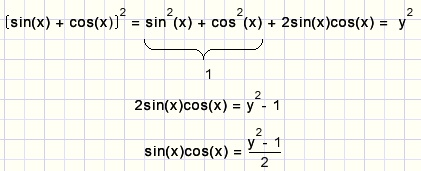
Verder.
Om schrijfwerk te besparen noemen we de wortel uit 24/25 even p.
Daarna passen we de ABC formule toe:
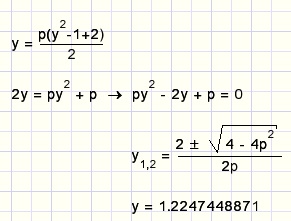
Nu nog een paar standaard goniometrie truukjes:
Merk op: cos(30) = y/(2sin(45))
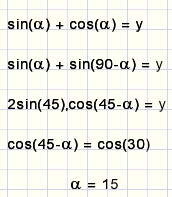
Hetzelfde antwoord als we grafisch vonden.
Het laatste stukje:
AD = AF + FD = 5 + 5.tan(15) = 6,34....
AB = 5 + 5/tan(15) = 23,66.....
AB*AD = 150.
Het geel gekleurde oppervlak is 150-25-24 = 101.
Mooie puzzel.

