de Formule Kraker van graphics-explorer

Het project

Dit artikel beschrijft het vertalen van verschillende soorten wiskundige vergelijkingen
in en reeks elementaire rekenkundige operaties.
Dat proces heet ook wel "parsing".
Het is nodig als grafieken getekend moeten worden of wanneer formules in een spreadsheet worden gebruikt.
Jaren geleden maakte ik al eens zo'n programma voor mijn grafiekenprogramma Graphics-Explorer.
Bij nadere beschouwing echter, is deze Delphi code lastig te lezen.
Daarom heb ik het programma herschreven in een meer begrijpelijke vorm.

Het Delphi-7 project bestaat uit 3 units:
    - unit1: form met buttons, TEdit component voor de formules, een paintbox voor grafieken of tabellen
    - xlate: hier staat de code voor de vertaling van de formules
    - eqdrawer: bevat de procedures om de verschillende grafieken te tekenen
Form1 en unit1 vormen samen een simpele exerciser om de vertaling te testen.
xlate bevat ook debug code, die aan- of uitgezet kan worden.
Deze debug code voorziet in het tonen van de tabellen die tijdens het vertaalproces worden opgebouwd.

Click [ hier ] om het exerciser programma te downloaden.
Click [ hier ] voor het gehele Delphi-7 project.
Click [ hier ] voor de source listing van de xlate unit.

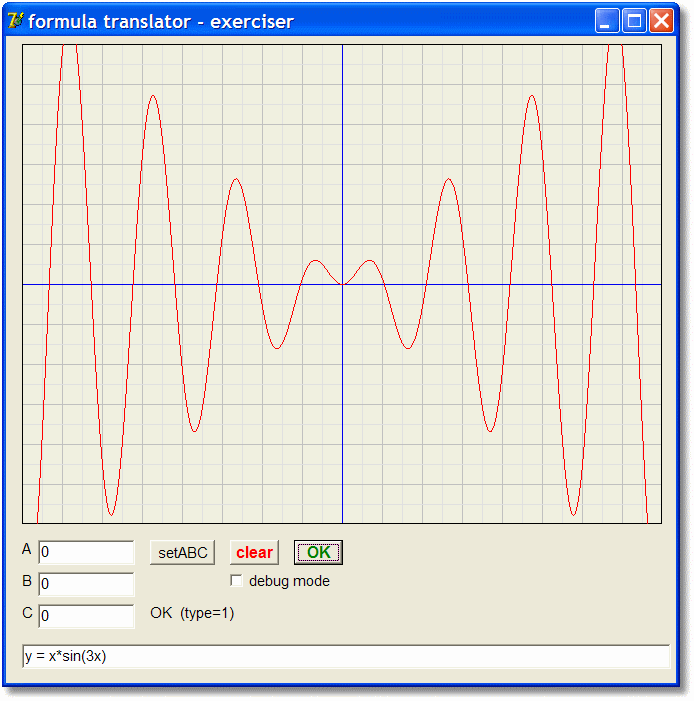
Hieronder staat een afbeelding van de exerciser in bedrijf. Getoond wordt de functie y = x*sin(3x)

Donaties

Ontwerpen van software kost veel tijd.
Deze software bied ik gratis aan.
Wordt er echter commercieel gebruik van gemaakt, wees dan zo vriendelijk een bedragje
voor mijn website te doneren

Formules, Vergelijkingen en Functies

Een formule is een berekening waar nog onbekende getallen in voor komen.
Die onbekende getallen duiden we aan met een letter.
Een voorbeeld is de formule voor het volume V van een bol met straal R:....... V = (4/3)pR3
Hierin is p een constante (3,14.......) en R is een variabele.
Door substitutie van p met genoeg cijfers voor de gewenste nauwkeurigheid
en R voor de lengte van de straal, kan V worden berekend.

In het voorbeeld hierboven is R de onafhankelijke variabele (we kunnen R elke positieve waarde geven) en
V is de afhankelijke variabele.
Als we niet weten waar de berekening op slaat, dan is het gebruikelijk om de onafhankelijke variabele x
en de afhankelijke y te noemen.

De vorm .....y = ....één of andere formule met x...... heet een functie.
Voor elke waarde van x kan de bijbehorende waarde van y worden berekend.
Elk paar (x,y) kunnen we als punt tekenen in een coördinatenstelsel.
Al die punten vormen tesamen de grafiek van die functie.

De vorm ....x = ....een formule met y ........heet een inverse (omgekeerde) functie.
Bij elke waarde van y kan x worden berekend.
Opmerking: een inverse functie ontstaat door de grafiek te spiegelen om de lijn y = x

Functies kunnen nooit een cirkel als grafiek hebben, omdat in het geval van een cirkel
per x twee waarden van y optreden.
In dat geval kan echter een parameterfunctie worden gebruikt.
De truuk is hier, dat zowel x als y een functie zijn van een derde variabele (hier genoemd v).
Met mijn vertaalprogramma kan simpelweg worden geschreven:
    y = 5sin(v) ; x = 5cos(v) ........om een cirkel te tekenen met middelpunt (0,0) en straal 5
In zeldzame gevallen zoals de grafiek van een trifolium, bestaan er geen functies.
De grafiek is dan het resultaat van een (ingewikkelde) vergelijking
    .....x.....y.... = ....x....y......
Links en rechts staat een formule met x en/of y.
Bovenstaande vergelijking is te schrijven als .....x......y...... = 0 en deze vorm heet een impliciete functie.
De cirkel hiervoor is ook te schrijven als x2 + y2 = 25

De grafiek is de verzameling van alle puntenparen (x,y), waarvoor de vergelijking klopt.
Mijn vertaalprogramma herkent ook dit type vergelijkingen maar het tekenen van de grafiek kost iets meer tijd.
y = 2x - 5 geeft dezelfde grafiek als y - 2x = 5 maar de laatste duurt langer.

Alle typen functies (normaal, inverse, parameter, impliciet) gebruiken hetzelfde vertaalprogramma en genereren dezelfde tabellen.
De procedures voor het tekenen van de grafieken zijn echter verschillend.

Samanvatting van de ondersteunde functies:
    typenaamvoorbeeldbetekenis
    1normaaly = 3x2 -2x + 1parabolische functie
    2inversex = 3sin(y)inverse sinus functien
    3parametery = 3sin(x) ; x = 3cos(x)cirkel
    4implicietx2 + y2 = 9zelfde cirkel als bij type 3

Operatoren en prioriteit

Een berekening zoals 1 + 3*2 + 5*32 kan niet simpelweg gemaakt worden van links naar rechts,
omdat de berekeningen niet dezelfde prioriteit (voorrang) hebben.
Ook hebben berekeningen tussen (.......) voorrang zoals in 3*(10 -6) waar 10 - 6 als eerste berekend moet worden.
In de tabel hieronder staan alle bewerkingen met hun prioriteit:
    naamsymboolprioriteitvoorbeeld
    functie...7log(x)
    machtverheffen^6x^3
    unaire --5-sin(x)
    vermenigvuldigen*43*x
    delen/4x/5
    optellen+3x+5
    aftrekken-3x/5
    waarde geven=2y = 17
    scheiding;1y = 1; x = 2
Opmerking: de ; operator is een dummie (geen echte) met de laagste prioriteit.
Het houdt de x en y waarden gescheiden in parameter functies.

Een impliciete functie (type 4) zoals .......x^2 + y^2 = 15x + 22y wordt tijdens de vertaling
omgebouwd tot de vorm ....v = (x^2 + y^2) - (15x + 22y)
De - operator krijgt dan prioriteit 2, de = operator prioriteit 1.
Zodoende geldt dat v = 0 als (x,y) de vergelijking kloppend maakt.

Het type vergelijking vaststellen

De vertaler wordt aangeroepen met
    procedure xlateEquation(s : text; var xcode: byte);
s is de formule tekst.
xcode is 0 als de vertaling succesvol was en ongelijk 0 voor een bepaalde fout.
Voordat het vertalen begint wordt de tekststring omgezet naar lower case en gekopieerd naar string "basetext".
Ook wordt aan het eind een spatie toegevoegd om het eind van de string te markeren.
xlateEquation(..,..) roept dan procedure detecttype aan om het type vergelijking vast te stellen.

Detecttype telt het aantal x , y, = en ; tekens en legt hun positie in de string vast.
Spaties tellen hierin niet mee.
Een array heeft kolommen voor de tekens x, y, = en ;
Als een x op positie 1 van de string staat, dan wordt een 1 geschreven op de eerste vrije plaats van de x kolom.
Als er een ; staat op positie 15 in de string, dan wordt 15 geschreven in de kolom van het ; teken.
Een kolomhoogte is dus gelijk aan het aantal aangetroffen tekens van dat soort.

Detectie van een type 1 functie:
    - slechts 1 y op positie 1 {spaties niet gerekend}.... en
    - slechts 1 = op positie 2 ....en
    - geen ;
Detectie van een type 2 functie:
    - slechts 1 x op positie 1.......en
    - slechts 1 = op positie 2........en
    - geen ;
Detectie van een type 3 functie:
    - 1 ; ....en
    - 2 = tekens ......en
    - slechts 1 x op positie 1....en ... slechts 1 y na de ;.....of
    - slechts 1 y op positie 1....en ... slechts 1 x na de ;
Detectie van een type 4 vergelijking:
    - geen type 1,2,3 ..........en
    - geen ;.........en
    - slechts 1 =
Zie de source code voor details.
Array cp[x...; , rows] bevat de posities van de tekens x, y, =, ;
Array cc[x..;] bevat het aantal tekens per kolom van cp[ ]

Data Structuren

De getallen voor alle berekeningen worden opgeborgen in array REG[1..67] of double.
Hieronder staan de toewijzingen:
    register nummer doel
    1..29tussenresultaten van berekeningen
    30..59constanten in de formule tekst
    60x
    61y
    62v
    63a
    64b
    65c
    66pi
    67e
a,b,c zijn constanten. Hun waarde mag worden veranderd zonder dat de formule opnieuw vertaald hoeft te worden.
pi = 3.14.... en e is de basis van de natuurlijke logaritme.

Operators en functies krijgen een code:
    codebewerkingnaam
    1+optellen
    2-aftrekken
    3*vermenigvuldigen
    4/delen
    5^machtverheffen
    6-unaire -
    7=waarde geven
    8;scheider
    9not used.
    10sinsinus
    11coscosinus
    12tantangens
    13asininverse sinus
    14acosinverse cosinus
    15ataninverse tangens
    16sqrtvierkantswortel
    17loglogaritme grondtal 10
    18lnlogaritme grondtal e
    19expmacht van e
    20absabsolute waarde
    21intafronding op helen

De Postfix Table

Dit is een tijdelijke tabel in het vertaalproces.
Procedure makePFT maakt de tabel.
De entries zijn van het type TPostfix: 
type TPostfix = record
                 reg      : byte;
                 opcode   : byte;
                 priority : byte;
                end;
				
const maxPFT     = 60;	

var PFT       : array[1..maxPFT] of TPostFix;
    pfti      : byte; //#entries in PFT
Het bouwen van de postfix table volgt op het vaststellen van het type functie.
Tegelijk met het bouwen van de tabel worden ook:
    - constanten in registers 20...59 gezet, in de volgorde van optreden
    - * operatoren ingevoegd tussen
      - )(
      - constanten of variabelen en (.....voorbeeld: 3( --> 3*(........of .....x( --> x*(
      - constanten of variabelen en ).....voorbeeld: )3 --> )*3........of......)x --> )*x
      - constanten en functies ......voorbeeld: 3sin(x) --> 3*sin(x)
      - variabelen en constanten.......voorbeeld: 3x --> 3*x .. of x3 --> x*3
    - de syntax getest
In TPostfix is:
    reg.........het register nummer
    opcode...de code van de bewerking (operation), zie tabel hiervoor
    priority....de prioriteit van de bewerking
De prioriteit is de som (optelling) van de biaspriority (variabele biasprio) en de prioriteit van de bewerking.
De biaspriority wordt met 10 verhoogd na een ( openings haakje en met 10 verlaagd na een ) sluitings haakje.
Dus, x + 3 heeft prioriteit 4, maar (x + 3) heeft prioriteit 14.

Een nadere blik op een string met een vergelijking onthult de algemene vorm:
    | variabele of constante | operator | variabele of constante | operator | ......................
In de postfix notatie wordt de string geschreven als
    | variabele of constante | operator |
    | variabele of constante | operator |
    | variabele of constante | operator |
    ............................
Dan wordt een derde kolom toegevoegd met de prioriteit van de bewerking.
Reden is dat later de bewerking met de hoogste prioriteit geselecteerd kan worden.

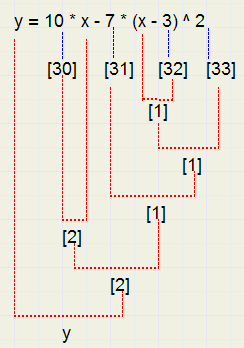
Hieronder staat een voorbeeld hoe de Postfix table (PFT) eruitziet na vertaling van
............. y = 10x - 7(x-3)^2:
    regopcodepriority
    y=2
    [30]*4
    x-3
    [31]*4
    x-13
    [32]^6
    [33]...0
Opmerking: constanten zijn opgeborgen in registers 30,31,....in de volgorde van optreden in de string.
[30] = 10, [31] = 7, [32] = 3, [33] = 2

We kijken wat gedetailleerder naar het bouwproces van de tabel.
De tekens van string basetext worden in groepjes ingedeeld:
    'a' ...'z'
    '0'..'9', decimal point
    (
    )
    =
    -
    + * / ^
    space
    ;
De formule string basetext wordt teken voor teken gelezen.
Een case statement voert procedures uit afhankelijk van de groep waartoe het teken behoort.
Actie hangt af van de huidige omstandigheden en/of wat eerder werd aangetroffen.
Dat laatste wordt bijgehouden met de variabele scan : 
type Tscan = (scNone,scAlphaScan,scNumScan,scConstant,scVariable,scFunction,
              scOperator,scOpen,scClose);
    scNone:niks gebeurd....{na start, na = of ; }
    scAlphascan:tijdens lezen naam van variabele of functie
    scNumscan:tijdens lezen van een getal
    scConstant:getal gevonden
    scVariable:variabele gevonden
    scFunction:functie gevonden
    scOperator:operator gevonden
    scOpen:( gevonden
    scClose:) gevonden
Dus, een gelezen teken wordt aangeboden aan een case statement, dat de groep van het teken vaststelt.
Voor elke groep is er vervolgens een nieuw case statement dat de staat van de scan variable test.
Dan wordt een bepaalde helper procedure aangeroepen om de Postfix table te bouwen.
Hier staan die helper procedures die het werk doen:
    procAlpha:test alpha string op variabele of functie. Maak register nummer of operator code.
    procNum:test numeric string op constante, zet constante in register
    procUminus:behandel unaire - zoals in ...( -x + 4)
    procOpen:verhoog biaspriority met 10
    procClose:verlaag biaspriority met 10
    multInsert:voeg * operator in voor vermenigvuldiging, zoals tussen ) (
De geneste case statements zorgen voor het testen van de syntax.

Voorbeeld:
procAlpha wordt aangeroepen als scan = scAlphascan
{we lezen tekens van basetext, die een variabele of functie kunnen zijn}
en we komen tegen:
spatie, ( , ) , cijfers , ; of een operator.
We bekijken de eerste regels van het case statement: 
 for i := 1 to length(basetext) do
  begin
   c := basetext[i];
   case c of
    '(' : begin
           case scan of
            scNumScan : procNum;
            scAlphaScan : procAlpha;
           end;
           case scan of
            scClose,
            scVariable,
            scConstant : multinsert;
           end;//case
           procOpen;
          end;// '('

    ')' : begin
           case scan of
            scOpen,
            scOperator,
            scfunction : errorcode := 7;
            scNumScan  : procNum;
            scAlphaScan: procAlpha;
           end;//case
          procclose;
          end;//')'
		  ......................
Opmerking: errorcode 7 is de code voor een syntax error.
In dit geval hebben we misschien gevonden ......sqrt) , wat fout is.

Opmerking:
na de procAlpha procedure is de scan variabele gelijk aan scVariable of scFunction, net wat er gevonden werd.
Na de procNum procedure, scan = scConstant.
Na multInsert , scan = scoperator

Zie de source code voor details.

De Director table.

Dit is de uiteindelijke tabel, het resultaat van de vertaling.
Procedure makeDRT bouwt deze tabel.
De xlateEquation procedure roept makeDRT aan als de Postfix table met succes is gebouwd.
Dat is het geval als errorcode = 0. 
type TDirector = record
                  opcode : byte;
                  dest : byte;
                  src1 : byte;
                  src2 : byte;
                 end;
				
const maxDRT = 60;	

var DRT    : array[1..maxDRT] of Tdirector;
    dix    : byte;//index for DRT during calculations
    valid  : boolean;//during calculations
    DRTtop : byte; //#entries in DRT
De director table (DRT) bevat alle bewerkingen gesorteerd van hoogste naar laagste prioriteit.
dest is het destination (doel) register, src1 en src2 zijn de source (bron) registers.
In het geval van de Postfix table hiervoor { met ........ y = 10x - 7(x-3)^2 } , wordt de DRT:
    opcodedestsrc1src2
    -[1]x[32]
    ^[1][1][33]
    *[2][30]x
    *[1][31][1]
    -[2][2][1]
    =y...[2]
Het plaatje hieronder toont de berekeningen en tussenresultaten:
[1] betekent : klad register nummer 1.
Procedure makeDRT zoekt in de PFT naar de bewerking met de hoogste prioriteit.
Indien nodig wordt een kladregister toegewezen voor een tussenresultaat.
De bewerkingen en registers worden ingevuld in de DRT en die bewerkingen worden uit de PFT verwijderd.
makeDRT heeft 3 hulp procedures:
    function getfreeReg : bytereserveer een vrij kladregister
    procedure freeReg(k : byte)maak register (k) vrij voor toekomstige reservering
    procedure ShiftUpPFT(n : byte)shift [n+1] --> [n], [n+2] --> [n+1] ......
variable regreserve heeft bit i geset(1) als register i vrij is.
Voorafgaand is regreserve gezet op waarde $3ffffffe, wat alle kladregisters 1..29 vrij maakt

Neem eens aan, dat regel j van de PFT de bewerking met de hoogste prioriteit bevat.
Dat krijgt source operand 1 (src1) van de DRT entry de waarde van reg van regel j van de PFT.
Source operand 2 (src2) krijgt de waarde van reg van regel j+1 van de PFT.
De opcode in DRT wordt de opcode van regel j van de PFT.
En wat is het dest (destination) register in the DRT?
    - als één van de source operands een kladregister is, dan is dest datzelfde kladregister.
    - als beide (src1 en src2) kladregisters zijn, dan wordt src1 het dest register.
    - als beide registers variabelen of constantes zijn, dan wordt een vrij kladregsiter toegewezen voor dest.
    - als reg = x,y of v in regel j van de PFT, dan is dest in de DRT dezelfde x,y of v ........{x = 3 bijvoorbeeld}
De situatie wordt gecodeerd in variabele regcode waarna een case statement regcode test.
Opmerking: in het geval van een functie of unaire - , is het reg veld in de PFT gelijk aan 0.
De operand wordt dan gevonden in veld reg van de volgende PFT regel.
Functies en de unairy - gebruiken alleen src2, src1 = 0.
Nadat de PFT is opgeschoven om de gaten te dichten van de verwijderde bewerkingen
die aan de DRT werden toegevoegd, krijgt het PFT reg veld field de waarde van het destination register.

Laten we bovenstaande vergelijking stap voor stap behandelen,
waarbij de PFT wordt afgebroken en de DRT opgebouwd.
{y = 10x - 7(x-3)^2 }
    Postfix table PFTdirector table DRT
    regopcodepriority
    y=2
    [30]*4
    x-3
    [31]*4
    x-13
    [32]^6
    [33]...0
    opcodedestsrc1src2
    -[1]x[32]
Klad register 1 ontvangt het resultaat.
    Postfix table PFTdirector table DRT
    regopcodepriority
    y=2
    [30]*4
    x-3
    [31]*4
    [1]^6
    [33]...0
    opcodedestsrc1src2
    -[1]x[32]
    ^[1][1][33]
register 1 bevat het resultaat
    Postfix table PFTdirector table DRT
    regopcodepriority
    y=2
    [30]*4
    x-3
    [31]*4
    [1]..0
    opcodedestsrc1src2
    -[1]x[32]
    ^[1][1][33]
    *[2][30]x
register 2 bevat nu een tweede tussenresultaat
    Postfix table PFTdirector table DRT
    regopcodepriority
    y=2
    [2]-3
    [31]*4
    [1]..0
    opcodedestsrc1src2
    -[1]x[32]
    ^[1][1][33]
    *[2][30]x
    *[1][31][1]
    Postfix table PFTdirector table DRT
    regopcodepriority
    y=2
    [2]-3
    [1]..0
    opcodedestsrc1src2
    -[1]x[32]
    ^[1][1][33]
    *[2][30]x
    *[1][31][1]
    -[2][2][1]
    Postfix table PFTdirector table DRT
    regopcodepriority
    y=2
    [2]..0
    opcodedestsrc1src2
    -[1]x[32]
    ^[1][1][33]
    *[2][30]x
    *[1][31][1]
    -[2][2][1]
    =y...[2]
En de vertaling is gereed.

Gebruik de exerciser in debug mode om de PFT en DRT van andere vergelijkingen of functies te zien.

Syntax

Syntax checking vindt plaats tijdens de bouw van de PFT.
Hoofdregel is, dat er om en om operators en constanten, variabelen of functies moeten staan.
Twee opvolgende operators zoals - - 5 is niet toegestaan. Wel goed is - (-5).
Ook OK is : y = - x ........of.......... y = - cos(5x), - is hier een uniare operator.
Houd in gedachten het verschil tussen - 2^4 { = - 16} en (-2)^4 { = 16}
Na een functie moet altijd een ( staan. Voorbeeld is ........ sin(3x).
De * vermenigvuldig operator wordt automatisch ingevoegd tussen )..( , getallen en variabelen of getallen en functies.
Voorbeelden:
    y = 3sin(x) .........y = 3*sin(x)
    y = (x-1)sin(x).........y = (x-1)*sin(x)
    y = sin(3x)............y = sin(3*x)
    y = (x-1)(x-2)............y =(x-1)*(x-2)
    y = a(x-1).............y = a*(x-1)
Haakjes binnen haakjes is toegestaan, maar het maximum is 20 haakjes (((((.... diep.
Er moeten evenveel ((( als ))) voorkomen aan elke kant van het = teken of het scheidingsteken ;

Het volgende is fout:
    y = xsin(x)............'xsinx' wordt niet herkend. Schrijf x*sin(x)
    y = ab..............'ab' wordt niet herkend, schrijf a*b
De vertaling levert een foutcode. Nul geeft aan dat de vertaling geen fouten opleverde.
Als de errorcode ongelijk 0 is, dan levert function getmessage(errorcode) een string met beschrijving van de fout.

Berekeningen

Nu de director table is gebouwd, kan simpelweg de waarde van een functie worden berekend.
De opdrachten in de DRT worden daarvoor regel voor regel uitgevoerd.
Na de vertaling mogen de waarden van a, b, c nog worden veranderd. Opnieuw vertalen van de formule is niet nodig.
In geval van een type1 functie, moet voor de berekening x een waarde krijgen.
Dat kan met een call van procedure setX(...).
procedure calculate(var OK : boolean) doet daarna het werk.
De OK flag is true na een foutvrije berekening.
OK is false na
    - delen door nul
    - logaritme van een negatief getal
    - overflow
    - wortel uit een negatief getal
Gebruik de getY functie om na berekening de y waarde op te halen.

Voor elke operator of functie is er een korte function die de berekening uitvoert.
een try....except....structuur vangt rekenfouten op.
Variabele dix is de index in de DRT. dis loopt van 1 tot DRTtop.

In geval van een type2 functie moet setY(..) worden gebruikt en na berekening getX.

Bij een type3 functie wordt dat setV(..) en na berekening getX en getY.

Voor een type4 functie moeten zowel x als y eerst een waarde krijgen en het resultaat van de berekening staat in v.
Call getV.
Houd in gedachten, dat een type4 vergelijking zoals x2 + y2 = 25, veranderd wordt in
v = x2 + y2 - 25, met prioriteit 2 voor de - en prioriteit 1 voor de =
v is dus gelijk aan 0 als (x,y) een oplossing vormt.

De exerciser

De exerciser bestaat uit form1 en unit1.
Het voorziet in een TEdit om formules in te tikken en knoppen om de vertaling te starten
of de constantes a,b,c in te voeren.
Ook is er een checkbox om naar debug mode over te schakelen.
In dat geval wordt geen grafiek getoond, maar de tabellen.
De exerciser is simpel van opzet gehouden.
Zo ligt het coördinatenstelsel in paintbox1 vast, met (0,0) op pixelpositie (320,240)
x loopt van - 8....+8 en y van -6....+6. De schaal is 40 pixels per cm.

Kijk op fxlate2.html voor een beschrijving van de teken procedure van elk type functie.