exponentiële functies berekenen

Exponentiële functies berekenen

	download exerciser programma
	download hele Delphi-7 project
	bekijk de source code

Inleiding

Dit artikel beschrijft een methode van expontiële curve fitting,
zoals toegepast in Graphics-Explorer, mijn grafieken programma.
Een bijgevoegd exerciser programmma toont stap voor stap de uitvoering van het proces.

De curve fitter berekent de best passende exponentiële functie bij een verzameling punten.
De functie is

y = a.b^x + c

hierin zijn a,b,c de parameters.

Inhoud

exerciser beschrijving

curve fitting theorie

project beschrijving

Exerciser beschrijving

Hieronder staat een verkleinde afbeelding van de exerciser in actie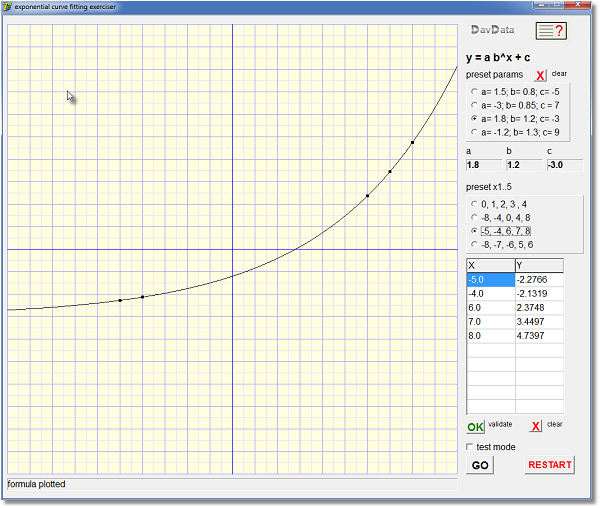

a,b,c		berekende parameters. (zwart: OK; rood: ongeldig)
preset params		klik radio knop om parameters te kiezen
preset x1..x5		klik radio knop om punten te kiezen
x, y		lijst van punten, maximaal 10
[OK] validate		klik om punten te sorteren en te controleren
[GO]		start berekening van parameters a,b,c
[ ] testmode		vink aan voor stap voor stap uitvoering

Bediening

Punten zijn toe te voegen door:

Opmerking: SHIFT toets indrukken bij muisklik geeft pixel nauwkeurigheid.
Anders afronding op veelvoud van 10 pixels.
Na verandering van punten moet de [OK] knop worden geklikt.
Voor stap voor stap uitvoering van de berkeningen, vink de [testmode] checkbox.
Klik dan de [GO] knop om a,b,c te berekenen en de functie te plotten.
Voor het verwijderen van punten of parameters: klik de bijbehorende [X] knop of [RESTART].

Curve fitting theorie

Input voor de curve fitter is a verzameling punten [x₁,y₁]....[x_n,y_n]
Het minimale aantal punten is 3.
Het maximale aantal is 10.
De curve fitter berekent de parameters a,b,c zo, dat de functie y = a.b^x + c de kleinste afstand tot de punten heeft.

Interne berekeningen gebruiken de functie y = a.e^bx + c ........... (e^b wordt later b)
De methode heeft een numerieke en een analytische component.
Dit zijn de stappen:

^bx

least square

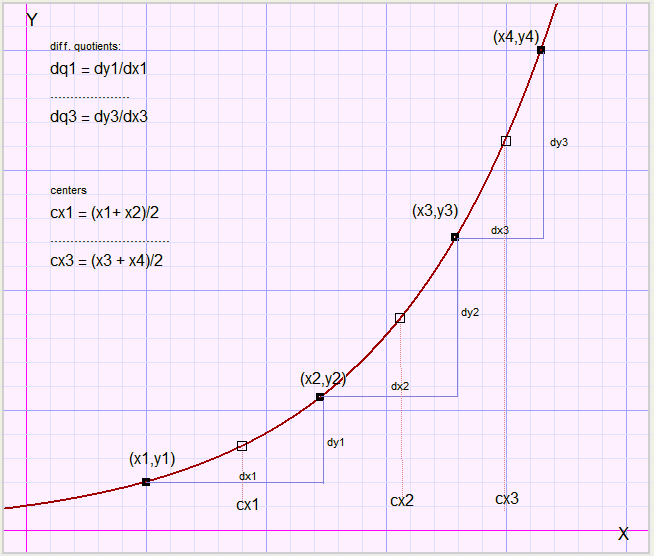
Benadering van b

array dx bevat de x afstanden tussen opvolgende punten
dx1 = x2 - x1....dx3 = x4 - x3

array dy bevat de y afstanden
dy1 = y2 - y1....dy3 = y4 - y3

array cx bevat de x middens tussen de punten
cx1 = (x1+x2)/2....cx3 = (x3+x4)/2

array dq bevat de differentie quotienten
dq1 = dy1/dx1....dq3 = dy3/dx3

Opmerking: in Delphi wordt cx1 geschreven als cx[1]...enz.

uitgaande van

^bx

dat elimineert c.
Zodat we kunnen schrijven

₁

^bx₁

₂

^bx₂

₃

^bx₃

Parameter a is te elimineren door opvolgende y' waardes te delen:

₂

₁

^b(x₂-x₁)

₂

₁

₂

₁

met bovenstaande in gedachten:

The middenwaardes van x (cx) worden gebruikt, omdat de afgeleide daar het nauwkeurigst is.
Voor de opvolgende punten wordt een gemiddelde waarde van b berekend.
Dit is de benadering van b.

Benadering van a

Uitgaande van

₁

^bx₁

₂

^bx₂

elimineren we c met het verschil tussen opvolgende rijen:

₂

₁

^bx₂

^bx₁

^bx₂

^bx₁

^bx₃

^bx₂

Een gemiddelde waarde van a wordt berekend.
Dit is de benadering van a.

Benadering van c

^bx

We mogen schrijven

₁

^bx₁

₂

^bx₂

Een gemiddelde waarde van c wordt berekend.
Dit is de benadring van c.

Intermezzo

In functie

zal de waarde van y met een factor g toenemen als x met 1 wordt verhoogd.
g heet de groei factor.

Exponentiële functies (met c=0, de x-as is de horizontale asymptoot), zijn het resultaat
van constante relatieve groei.

In de functie

^bx

zien we dat g = e^b.
b heet de relatieve groei snelheid omdat y'/y = b.e^bx/e^bx = b

Dus, een functie met relatieve groeisnelheid b, heeft een groeifactor g = e^b
waarin e de basis is van de natuurlijke logaritme. (e = 2.71828....)

Hiervoor verkregen we een benadring van c zodat we kunnen schrijven ...y - c = ae^bx
Als de punten (x1,y1)...(xn,yn) op een exponentiële functie liggen,
dan zullen we voor opvolgende punten steeds dezelfde groeifactor vinden.
De volgende stap, fijnstemming van c, gaan we c variëren om de kleinste afwijking
van de groeifactoren te vinden.

Fijnstemmen van c

We vergeten de eerder berekende a en b waarden en gaan verder met c en de punten [x1,y1]...[xn,yn].

Voor een waarde van c kunnen we schrijven

₁

^bx₁

₂

^bx₂

deling elimineert a

₂

₁

^b(x₂-x₁)

₂

₁

₂

₁

₂

₁

₂

₁

Twee opvolgende punten produren een waarde van ee.
Deze ee waardes worden gesommeerd in AVG, voor nu is AVG = ee1 + ee2 + ....
De groeifactoren worden bewaard in array growthfactor:
growthfactor1 = e^ee/dx1..........

Sommeren van de ee waardes sommeert eigenlijk b.dx1 + b.dx2 + b.dx3... = b(last X - first X)
Dus b = AVG / (last X - first X)
De gemiddelde groeifactor is e^b

^{AVG/(lastX-firstX)}

Nu moeten we de groeifactor waardes met AVG vergelijken.
Deviation = abs(AVG-growthFactor1) + abs(AVG-growthfactor2) + ......
Deviation is het result van procedure deviation , aangeroepen voor een bepaalde waarde van c.

Kleinste Kwadraten methode

De kleinste kwadraten methode is een algoritme dat de best passende veelterm
y = c₀ + c₁x + c₂x²+ ....berekent bij een verzameling punten.
In dit geval gaat het om een veelterm van de eerste graad.
Met een definitieve waarde van c in gedachten schrijven we

^bx₁

^bx₂

₁

₂

hetgeen een lineaire fuctie voorstelt, zoals y = a + bx.
We geven de punten (ln(y_i-c),x_i) aan de kleinste kwadraten methode, die de beste waardes van a en b berekent.
Resulterende a wordt vervangen door e^a om de ln( ) functie teniet te doen.

De kleinste kwadraten methode is een fraaie toepassing van de lineaire algebra.
Kijk [hier] voor een beschrijving met voorbeeld.

Aborts

De deviation procedure levert een abort als c tussen y waardes in ligt.
In dat gval snijdt de lijn y = c de curve.
c moet buiten het y bereik liggen.

Een negatieve waarde van ee laat geen ln functie toe.
Hieronder staat de flowchart voor de berekening (fijnstemming) van c

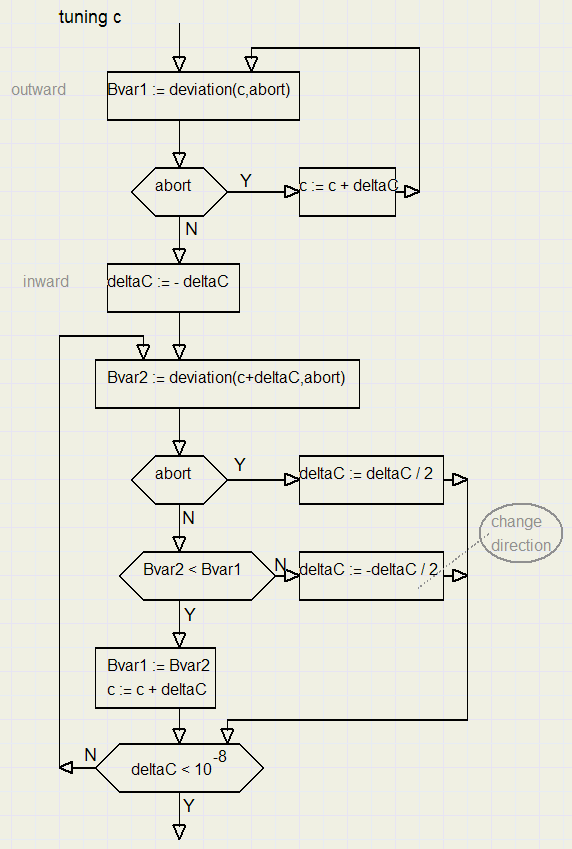
DeltaC is waarde waarmee c wordt veranderd.
Het proces stopt als deltaC heel klein is geworden.

Waakhond tijdklok

Procedure morepointsexp controleert de berekening van de a,b,c parameters.
Floating point berekeningen staan tussen try...except opdrachten.
Er zijn twee gevallen voor een abort:
1.Illegale Floating point operatie
Dit treedt op als punten te ver uiteen liggen om een exponentiële functie te maken,
een voorbeeld hiervan is (1,1) , (5,5) , (8,2)

2.C slaat op hol
Als c te ver weg ligt, dan zal een nog verdere positie een kleinere afwijking van de gemiddelde groeifactor opleveren.
C wordt dan steeds ten onrechte verhoogd en "slaat op hol".
Waakhond w beëindigt dit proces.
Fijnstemming van c krijgt maximaal 100 stappen, anders wordt het proces gestopt.
Deze situatie treedt op bij scherpe bochten.

Het Delphi-7 project

Er zijn 4 units en 1 form:

Unit1

Grafieken worden getekend in bitmap map, punten in paintbox1.
Afmetingen zijn 800*800 pixels, coordinaat (0,0) ligt op positie (400,400).
x domein is -10< x < 10,.........y bereik is -10< y <10.
De schaal is 40:1.
Er zijn twee belangrijke vlaggen:

Bij paramsOK = true, plot [GO] de functie.
Bij paramsOK = false, berekent [GO] nieuwe waardes van a,b,c en plot de functie.
Als a,b,c niet met de plot overeenkomen, dan worden ze in rood aangegeven.

Voor details verwijs ik naar de source code.

Unit2

procedure makeExpFunction doet het werk.
Punten worden opgehaald uit unit1 en opgeslagen in array Epoints[ ] van type Tpnt.

type TPnt = record
             x,y : double;
            end;

procedure deviation berekent de variatie van de groeifactoren voor de fijnstemming van c.
Deze waardes staan in variabelen Bvar1,Bvar2.

Unit3

Unit2 roept procedures aan in unit3 om de stappen in het curve fitting proces te tonen.
Deze informatie wordt in form1 paintbox1 geschreven.
waitflag : boolean (in unit1) controleert de stapsgewijze uitvoering.
Als waitflag = true, dan voert het programma processmessages procedures uit.

Unit4

Deze unit bevat de procedures van de kleinste kwadraten methode.
Aanroep van procedure buildexp12(var pp : Tpoints; maxp : byte) doet het werk,
pp verwijst naar de puntenlijst en maxp is het aantal punten.

Hiermee beëindig ik deze beschrijving.