

 |
Hoe werkt een computer? (deel 1) |  |
 |
Inleiding
In dit artikel leg ik de basisprincipes uit van de digitale techniek.Zo krijgt de lezer een idee van de processen die zich binnen een computer afspelen.
Digitaal en Analoog
Informatie-overdracht met elektriciteit kan op twee manieren: analoog en digitaal.De eenvoudigste manier is analoog omdat het aansluit bij de praktijk.
Uit een luidspreker klinkt muziek.
Geluid is trillende lucht, de druk varieert heel snel. Hoe sneller, hoe hoger de toon.
Hoe groter het drukverschil hoe luider.
Analoog wil zeggen dat er een glijdende schaal wordt gebruikt. Elke signaalsterkte heeft betekenis.
De sterkte van het signaal bepaalt ook de sterkte van het geluid.
AM en FM radiozenders werken analoog.
Op een grammofoonplaat is muziek analoog vastgelegd als slingeringen van een groef.
Een horloge met wijzers kan je een analoog horloge noemen: elke stand van de wijzers heeft betekenis.
Hieronder zie je de grafiek een een analoog signaal
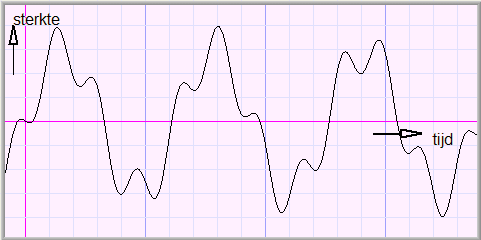
Digitaal betekent: met cijfers (digit is het Engelse woord voor cijfer).
Digitale apparaten werken met getallen: op een CD of DVD is de informatie opgeslagen als een rij getallen.
Bij de opname van zo'n CD moet een omzetting plaatsvinden van een analoog microfoonsignaal naar
een digitaal signaal.
Bij het afspelen van een CD moet het digitale signaal naar analoog worden omgezet waarna de eindversterker
stroom stuurt door de luidsprekers.
Hieronder zie je de grafiek van een digitaal signaal
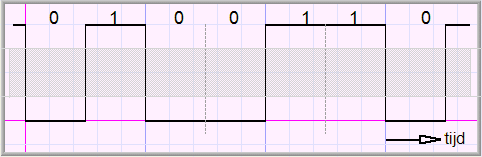
Er hebben maar twee signaalsterktes betekenis: boven de grijze zone "1" en onder de grijze zone "0".
Daarom kan ook signaaloverdracht plaatsvinden zonder vervorming: kleine afwijkingen in sterkte
hebben geen invloed zolang we maar uit de grijze zone blijven.
Omdat er wordt gewerkt met twee signaalsterktes is het tweetallig stelsel heel geschikt om te noteren
hoe een digitaal signaal eruit ziet. De ene sterkte noemen we "0" en de andere "1".
Bekijk dit artikel voor tellen en rekenen in het tweetallig stelsel.
In de grafiek hierboven zien we serie-overdracht van gegevens: de bits (nullen en enen)
worden door één draad na elkaar verzonden.
Dat is meestal het geval als tussen apparaten gegevens worden verzonden.
Binnen een apparaat vindt ook parallelle gegevensoverdracht plaats.
Er wordt bijvoorbeeld een getal van 8, 16, 32 of meer bits gelijktijdig verzonden over
evenzoveel parallel lopende draden.
Het zal duidelijk zijn, dat bij digitale signaalverwerking veel meer elektronische onderdelen nodig zijn
dan wanneer analoog wordt gewerkt.
Waarom al die moeite?
Er zijn twee redenen:
1. digitale informatie kan worden opgeslagen of gekopieerd zonder kwaliteitsverlies.
2. met getallen kan je rekenen, dus de informatie kan worden gemanipuleerd met wiskundige bewerkingen.
Digitale gegevensverwerking is mogelijk geworden door miniaturisering en kostenverlaging van de elektronica.
Variabelen
Een getal op zich zegt niets, er hoort altijd een verhaaltje bij.Neem de drie. Een gezin van drie kinderen? De score van een proefwerk? Buslijn 3?
Ook aan een bit (BInary digiT = tweetallig cijfer) moet een betekenis worden toegekend.
Het kan zijn dat een bit gewoon een cijfer is in een getal van 8,16 of 32 bits.
Het stelt dan een eenheid, tweetal, viertal, achttal enzovoorts voor.
Over die betekenis wil ik het nu niet hebben.
Welke wel?
Een bit kan twee waarden aannemen: '0' of '1'.
Die waarden kunnen we koppelen aan de betekenis "waar" (1) of "onwaar" (0).
Bij het bit hoort dan een bewering, bijvoorbeeld: "het is donker". Dat kan juist zijn (1) of niet (0).
Merk op, dat het gaat om een toestand die waar is of niet, schemering wordt niet meegerekend.
In deze redenering kan een deur ook niet op een kier staan. De bewering "de deur staat open"
is juist of niet.
Voor getallen die we nog niet weten schrijven we even een letter.
Voor een bit kunnen we dat natuurlijk ook doen.
De bewering "Jan is 16 jaar oud'' kunnen we A noemen.
A is dan een binaire variabele die de waarde 0 (niet waar) of 1 (wel waar) kan hebben.
Zo'n variable die de waarde "waar" of "onwaar" kan hebben heet een logische variabele.
Met een logische variable is natuurlijk niet te rekenen.
Maar we kunnen ze wel combineren en er formules ermee opstellen.
We betreden dan het gebied van de (propositie) logica.
Van het rekenen kennen we de bewerkingen +, - * en / voor optellen, aftrekken, vermenigvuldigen en delen.
Voor logische variabelen voegen we daar de logische bewerkingen "AND" , "OR" en "INVERSE" aan toe.
AND
Nederlands: "EN".Een kind vraagt aan zijn ouders het zakgeld te verhogen.
A = "vader gaat accoord".
B = "moeder gaat accoord".
In een "EN" gezin moet zowel A = 1 als B = 1 gelden, wil het verzoek ingewilligd worden.
Zowel vader als moeder moeten accoord gaan.
Noemen we de uitslag van het verzoek C, dan kunnen we schrijven .... C = A . B
Immers, C kan alleen maar 1 zijn als zowel A als B 1 zijn en 1 x 1 = 1.
Een elektronische schakeling die C maakt uit de signalen A en B heet een "AND" gate (gate = poort).
Hieronder staat het schema ervan.
Ernaast zie een grafiekje met de spanningniveaus van A, B en C.
Een AND combinatie is ook met schakelaartjes te maken door ze in serie te zetten.
We noemen de ingedrukte stand "1" en de niet ingedrukte- "0". De schakelaars zijn getekend in de "0"stand.
A = 1 betekent dat schakelaar A is ingedrukt en stroom doorlaat.
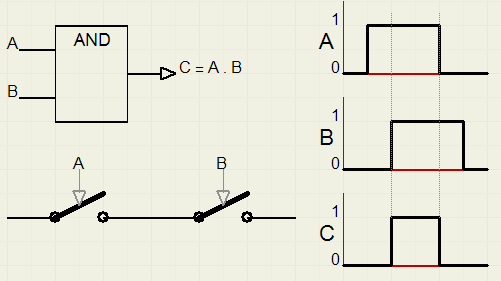
Merk op: een AND gate kent de tafels van vermenigvuldiging in het tweetallig stelsel.
"AND" is een logische functie en van logische functies is het verhelderend om een zg. waarheidstabel te maken.
Dat is een lijst waarin alle combinaties staan van de ingangssignalen met het resultaat.
Hieronder zie je de waarheidstabel van een AND functie van twee signalen:
A B C=A.B 0 0 0 0.0=0 0 1 0 0.1=0 1 0 0 1.0=0 1 1 1 1.1=1Snijmachines zijn gevaarlijk. Om te voorkomen dat iemand zijn vingers ertussen krijgt, moet de motor
worden aangeschakeld door twee in serie geplaatste schakelaars in te drukken.
Die schakelaars zijn dan zodanig geplaatst dat beide handen ver van de messen verwijderd zijn.
Opmerking: de AND functie heet ook wel logisch product
OR
Nederlands: "OF".Om terug te komen op het vragende kind hiervoor: het zou ook kunnen dat het kind zijn zin al krijgt als minimaal
één van de ouders instemt.
Dan geldt C = A or B. Voor de or bewerking wordt een + geschreven, zodat C = A + B.
Hieronder staat een zogenaamde or gate met de digitale signalen.
Eronder zie je hoe met schakelaars een or combinatie is te maken door ze parallel te zetten.
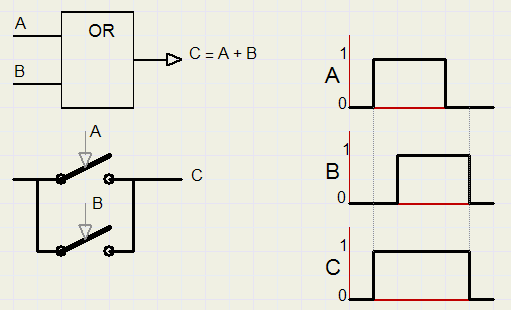
Voor zeer grote machines is het handig ze vanaf verschillende plaatsen aan of uit te kunnen zetten.
Om dat te bereiken kunnen de schakelaars parallel worden gezet.
Waarheidstabel van de OR functie van twee variabelen
A B C=A+B 0 0 0 0+0=0 0 1 1 0+1=1 1 0 1 1+0=1 1 1 1 1+1=1Opmerking: de OR functie heet ook wel logische som
Inverse
Dat is de omkering van een signaal: van "0" maken we "1" en van "1" een "0".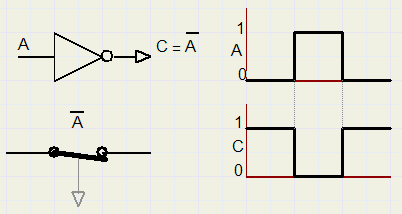
Een schakeling die het signaal omdraait heet een "inverter".
Hierboven zie je een rondje getekend aan de uitgang van de inverter: dat betekent dat er een "0" uitkomt
als er een "1" (geen rondje getekend) in gaat.
De schakelaar hierboven zal bij indrukken de stroom verbreken.
Het omgedraaide A signaal wordt aangeduid met een streepje boven de A.
A met een streepje erboven zal "1" zijn (waar) als A onwaar is.
hieronder volledigheidshalve de waarheidstabel
A niet(A) 0 1 1 0Hiermee zijn alle logische bewerkingen behandeld.
Digitale apparaten bestaan uit chips met miljoenen AND gates, OR gates en inverters.
Voorbeeld: de centrale verwarming
In een CV ketel wordt de gastoevoer ingeschakeld door stroom te sturen door een spoel dieeen magnetische klep opent.
Die klep moet worden geopend als
-
- de kamertemperatuur te laag is....EN
- de waterdruk hoog genoeg is......EN
- de keteltemperatuur NIET te hoog is
Daarom is op de ketel een TEST schakelaar T aangebracht om de gasklep direct open te zetten.
Deze schakelaar mag alleen door een service technicus worden bediend.
We zien hier een voorbeeld van serie- en parallelschakelaars, van EN en OF verbindingen.
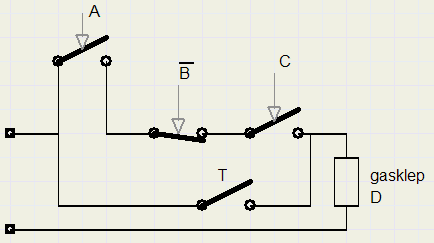
-
A : thermostaat, kamertemperatuur te laag
B : keteltemperatuur te hoog (fout, gevaar)
C : waterdruk in orde
T : testschakelaar
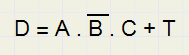
1.Een te hoge keteltemperatuur schakelt het gas uit. Dat voorkomt exploderen van de ketel
als zich stoom in de leidingen zou vormen.
Als B betekent "fout" dan is de inverse van B dus "goed".
2. Een te lage waterdruk voorkomt dat de vlam aangaat
3. De schakelaars zijn, zoals gebruikelijk, getekend in de niet-ingedrukte stand.
4. Muziekinstrumenten als een dwarsfluit of saxofoon hebben hulpgrepen.
Dat zijn grepen die in (EN, OF) combinatie met elkaar een klep openen of sluiten.
Computers werken elektronisch omdat daarmee de grootste snelheid wordt behaald.
Een kloknelheid van 2,4GHz (gigahertz) wil zeggen dat het kloksignaal 2400.000.000 maal
per seconde tussen de "0" en de "1" stand heen en weer schakelt.
In het techniek museum in Berlijn staat de ZUSE-1. Dat is een computer die volledig mechanisch werkt.
De EN en OF poorten zijn gemaakt van blikken plaatjes.
NAND en NOR gates
In de praktijk worden vaak poorten gebruikt die behalve een AND of OR functie het signaal ook omdraaien (inverteren).Zo'n omdraaiing wordt aangegeven met een klein rondje aan de in- of uitgang van de poort.
Een AND gate (gate = poort) die ook omdraait heet een NAND gate (not and).
Een OR gate die ook omdraait heet een NOR gate (not OR). Hieronder staan de schema's:
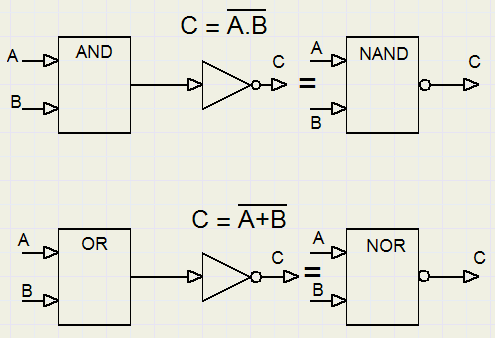
NAND NOR A B niet(A.B) A B niet(A+B) 0 0 1 0 0 1 0 1 1 0 1 0 1 0 1 1 0 0 1 1 0 1 1 0Een NAND gate geeft alleen een 0 uit als beide ingangen 1 zijn.
Een NOR gate levert een 0 af als één of meer ingangen 1 zijn.
Poorten met meer dan twee ingangen
In principe kan elke computer worden opgebouwd met alleen NAND (of NOR) gates met twee ingangen.Immers, zo'n poort kan alle noodzakelijke functie vervullen (AND,OR,inverse) zoals we nog gaan zien.
Maar handig is dat niet.
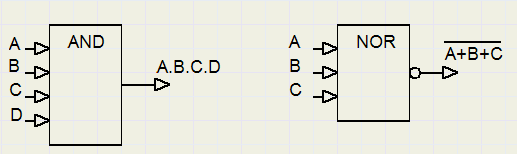
In de praktijk worden poorten gebruikt met 2, 3, 4 en soms 8 ingangen, zodat één poort veel meer signalen
kan combineren. Hieronder zie je twee voorbeelden.
de Wetten van De Morgan
Die luiden: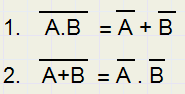
Het bewijs leveren we met waarheidstabellen:
1.
A B niet(A.B) niet(A)+niet(B) 0 0 1 1 0 1 1 1 1 0 1 1 1 1 0 02.
A B niet(A+B) niet(A).niet(B) 0 0 1 1 0 1 0 0 1 0 0 0 1 1 0 01. Produceert een 1 als er minstens één ingang 0 is, dus is te zien als een OR gate voor nullen.
2. Produceert een 1 als alle ingangen nul zijn, dus is te zien als een AND gate voor nullen.
Hieronder staan de schema's:
1.
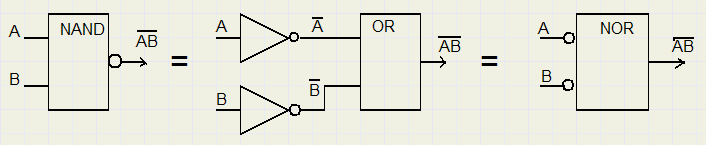
Bij een NOR functie voor nullen is één enkele 0 al voldoende om een 1 uit te geven.
2.
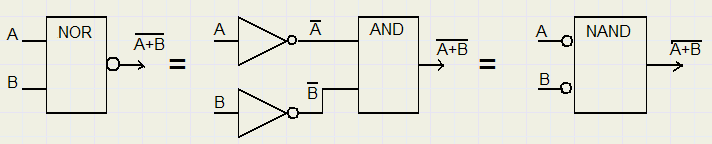
Beide ingangen moet 0 zijn om een 1 uit te krijgen.
Het voorgaande kan wat chaotisch overkomen, AND, OR, NAND, NOR, nullen en enen.
Daarom ga ik de notatie wat aanpassen.
De AND functie geef ik voortaan aan met een enkele letter A, de OR functie met een O.
Als de betreffende functie wordt vervuld voor een "0" dan teken ik aan de ingang van de poort een klein cirkeltje.
Aan de uitgang van de poort wordt een cirkeltje getekend als geen "1" maar een "0" wordt afgegeven als de AND
of OR functie wordt vervuld.
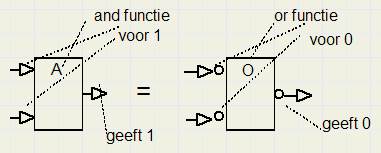
Een AND poort geeft een 0 uit als één of meer ingangen 0 zijn, dus vervult een OR functie
voor nullen.
Met inverters en een AND gate is als volgt een OR functie te maken:
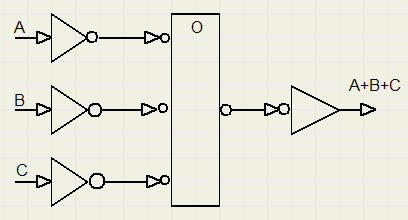
Met een OR gate en inverters is een AND gate te maken.
De lezer zal zich nu afvragen hoe je wijs kunt worden uit miljoenen gates.
Welnu, de tot dusver getoonde poorten zijn de eenvoudigste bouwstenen van digitale schakelingen.
Met die bouwstenen worden weer complexere bouwstenen gemaakt, enzovoorts.
Exclusive OR functie
De exclusive OR functie (XOR) is de belangrijkste bouwsteen van een schakeling die twee getallen kan optellen.De waarheidstabel is
A B A xor B 0 0 0 0 1 1 1 0 1 1 1 0De functie geeft een 1 als de ingangen ongelijk zijn.
Bekijk de waarheidstabel hierboven eens heel goed.
Het gaat dan om de regels die een "1" als resultaat hebben.
Zo'n regel is als een AND functie op te vatten, zoals niet(A).B {regel 2} en ook A.niet(B) {regel 3}
Regels met 1 als uitkomst vormen een OR functie, zodat een xor functie van A en B gelijk is aan
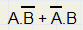
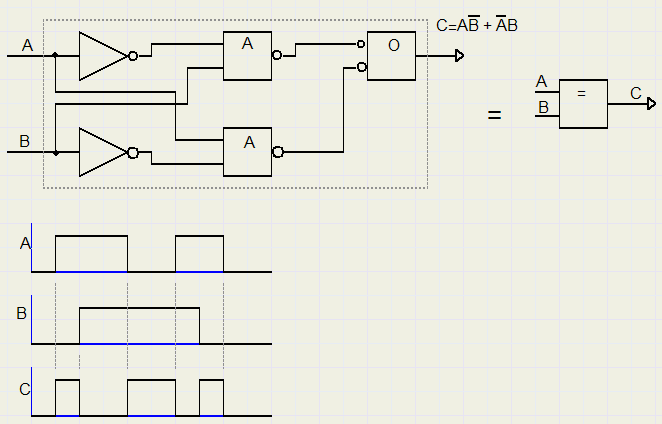
XOR heet ook wel logisch verschil (logical difference).
Weer een andere naam is "half adder", opteller zonder carry wordt daar mee bedoeld.
Opteller van twee 4 bits getallen
Laten we de optelling van twee bits een "stage" noemen (Engelse uitspraak).Een vier bits opteller heeft dan stage 0 (bits 0 van getallen a en b) t/m stage 3 (bits 3 van getallen a en b)
Wat speelt zich in zo'n stage af.
Welnu, in stage n komen de bits n van a en b binnen en ook de carry cin van de lagere stage.
Ook kan de stage een carry cout produceren naar stage n+1.
En natuurlijk wordt de som (sum) van a en b gemaakt
a b cin sum cout 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 0 1 1 0 1 1 0 0 1 0 1 0 1 0 1 1 1 0 0 1 1 1 1 1 1De som is 1 bij een oneven aantal 1 (a,b,c) bits in, dus twee xor poorten kunnen de som maken.
Een uitgaande carry treedt op als minstens 2 bits gelijk zijn aan 1.
Dus voor a.b en ook voor (a xor b) and c
Deze benadering is wat intuïtief, maar dat komt omdat we nog geen algebra hebben behandeld.
Hieronder het schema voor de optelling van twee bits met inkomende en uitgaande carry.
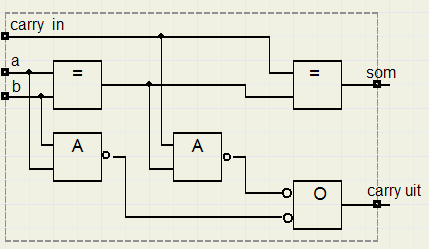
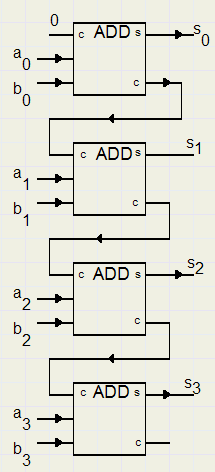
De ingaande carry van bit 0 is op 0 geforceerd.
Een dergelijke opteller is voor grotere getallengtes traag, want de carry moet in het ongunstigde geval door heel veel
poorten heen. Bijvoorbeeld bij de berekening 00000000000000001 + 0111111111111111 = 1000000000000000
Daarom worden er in een processor flink wat extra poorten tegenaan gegooid.
De opteller wordt verdeeld in groepjes van 4 bits.
Voor elk groepje worden in- en uitgaande carries parallel berekend.
Is de opteller heel lang, dan vormen 4 groepjes een segment, waarvan de carries ook weer parallel worden bepaald.
Een opteller zoals in het plaatje hierboven heet wel een "ripple adder" omdat de carry er doorheen "rimpelt".
Decoders
Een zeer veel voorkomende functie is de decoder. Processoren zitten er vol mee.Een decoder geeft een (1 bits) signaal dat aangeeft of een bepaalde conditie optreedt.
Stel dat we een telwerk hebben van 4 bits en we willen steeds weten wat de stand is.
De bits 0..3 noemen we a,b,c en d.
Hieronder staat de decoder:
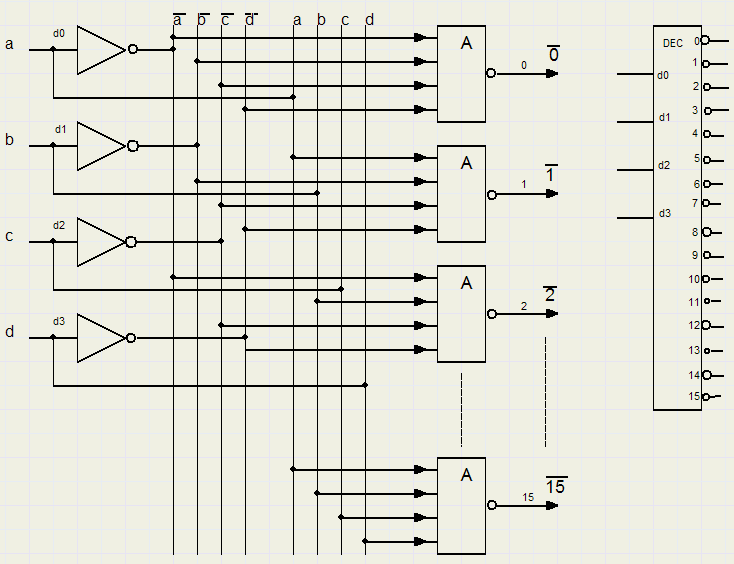
Rechts staat dezelfde decoder als blok getekend.
Multiplexers
Ook dit is een bouwsteen van een processor.Stel, dat we verschillende getallen willen optellen.
Een aparte opteller maken per twee getallen is omslachtig.
Beter is het om de getallen te kunnen selecteren als invoer voor een centrale opteller.
Laten we een 2 naar 1 (2:1) multiplexer nemen.
Hiermee kunnen we uit 2 bits (stel a en b) er 1 selecteren. Voor S=0 nemen we bit 0, voor S=1 bit 1.
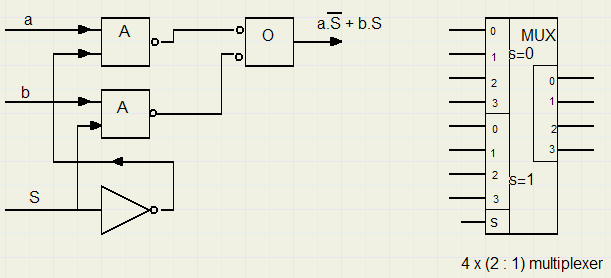
Hiermee zijn de meeste basisfuncties aan de orde geweest.
Een mooi moment om dit deel 1 te besluiten.
In een vervolgartikel wil ik de Booleaanse algebra behandelen en ook geheugens (Flip-Flops) en tellers.


