talstelsels

download
talstelsel
programma

Rekenen in andere talstelsels

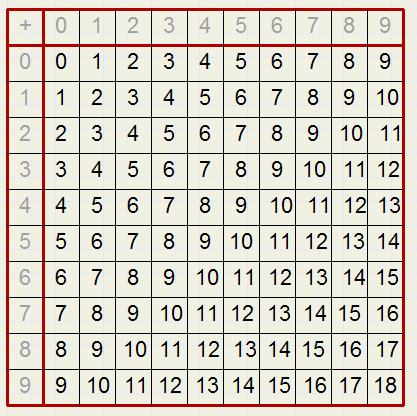
Ons 10-tallig stelsel

Wij rekenen in het tientallig stelsel.
Dat betekent dat er tien cijfers zijn (0,1,2,3,4,5,6,7,8,9) om getallen mee te maken.

Neem bijvoorbeeld het getal 725.
Het meest rechtse cijfer 5 geeft het aantal eenheden.
Links daarvan, de 2, zijn het aantal tientallen en het meest linkse
cijfer, de 7, zijn de honderdtallen. Enzovooorts.

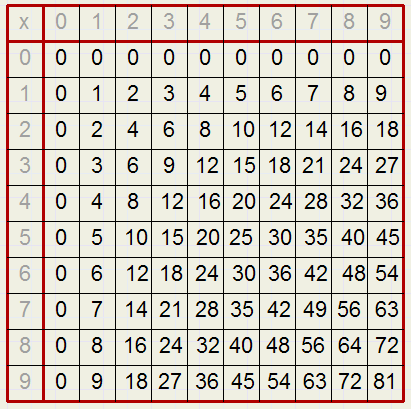
Om met potlood en papier berekeningen te kunnen maken hebben we twee tabellen nodig:

1. met de optellingen van elk twee cijfers

2. met de vermenigvuldiging van elke twee cijfers (de tafels geheten) :

Om berekeningen uit het hoofd te kunnen maken moet je deze twee tabellen uit het hoofd kennen.

We maken een paar berekeningen met potlood en papier.

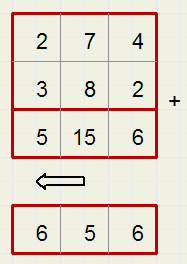
Eenheden worden bij eenheden, tientallen bij tientallen en honderdtallen worden bij hondertallen geteld.
Er zijn 15 tientallen, dat zijn 5 tientallen en 1 honderdtal.
Dat ene hondertal tellen we in het meest linkse vakje bij de honderdtallen.

Nu een voorbeeld met wat grotere getallen:

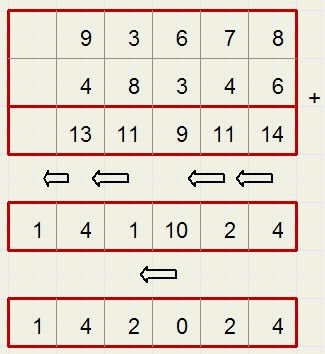
Nadat tientallen, honderdtallen enzovoorts zijn doorgeschoven blijker er nog 10 honderdtallen te staan.
We schuiven nog een duizendtal door om alle vakjes beneden de 10 te krijgen.

Nu de vermenigvuldiging 23 x 46.

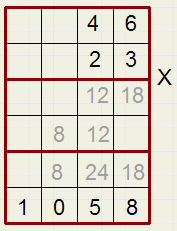
De tijdelijke waarden zijn in grijs weergegeven, de definitieve in zwart.
De uitkomsten van 3 x 6 of 2 X 4 zijn uit de (x) tabel af te lezen.

Tellen in het algemeen

Het bovenstaande zal je wel bekend voorkomen want op deze manier (ongeveer) wordt het rekenen
op de basisschool uitgelegd.
Maar aan rekenen gaat tellen vooraf.
Laten we daarom het tellen eens nader bekijken.

Het simpelste tellen is turven:

Alle berekeningen met gehele getallen kunnen met behulp van deze notatie worden gemaakt.
Wel kost dat bij grotere getallen veel tijd en zal het benoemen van die getallen een probleem vormen.
De manier van weergeven met aparte eenheden, tientallen, honderdtallen enzovoorts, is overzichtelijker
en ontstaat door het invoeren van een telmachientje:

Hierboven zie je dat telwerkje.
Door op het +1 knopje te drukken springt het naar de volgende stand.
Het indrukken van het knopje is als turven te beschouwen.
Het telwerk doorloopt zo de standen 0..1..2..3..4..5..6..7..8..9..0..1..2..3..4..5.......
Bij de overgang van 9 naar 0 geeft het telwerk een signaal af waarmee we een volgend telwerk kunnen bedienen.

Het signaal dat ontstaat bij de 9..0 overgang heet in rekentermen "1 onthouden".
In het Engels en in de computertechniek heet het "carry".

Volgens dezelfde regels als hierboven kunnen we in elk talselsel (vanaf 2) berekeningen maken.

Het 2-tallig stelsel

CD's en DVD's zijn in dit talstelsel gecodeerd.
Alle digitale apparaten, zoals computers, werken ermee vanwege de eenvoud.
Digitaal betekent "met digits" = met cijfers. Tweetallig heet ook wel "binair" (Engels: binary)

Een cijfer (0 of 1) in het 2-tallig stelsel wordt een "bit"genoemd.
Dat is een samentrekking van BInary en digiT.

Laten we met tellen in het tweetallig stelsel beginnen.
Bekijk het telwerkje hieronder:

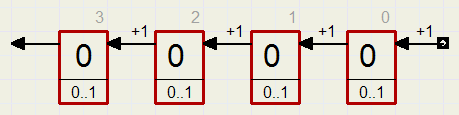
Bij herhaald indrukken van het knopje telt elk tellertje steeds 0..1..0..1..0..1..0..1..........
Bij de overgang 1..0 (over de kop gaan) wordt een signaal afgegeven dat de volgende teller aandrijft.
Zo onstaan achtereenvolgens de standen

	0 0 0 0 ... 0
	0 0 0 1 ... 1
	0 0 1 0 ... 2 
	0 0 1 1 ... 3
	0 1 0 0 ... 4
	0 1 0 1 ... 5
	0 1 1 0 ... 6
	0 1 1 1 ... 7
	1 0 0 0 ... 8
	1 0 0 1 ... 9
	1 0 1 0 ...10
	1 0 1 1 ...11 
	1 1 0 0 ...12
	1 1 0 1 ...13
	1 1 1 0 ...14
	1 1 1 1 ...15

(achter de tellerstand ...........is de decimale waarde aangegeven)

Nu maken we de som (+) en de product (x) tabellen:

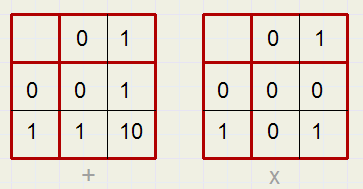Op de basisschool is veel tijd te besparen door alleen het tweetallig stelsel te leren.
De tafels van vermenigvuldiging zijn dan gekrompen tot 1 x 1 = 1 en verder niets.
Maar alles heeft zijn prijs: getallen worden al snel ontzettend lang.
Wie een paar schoenen koopt van € 255 moet daar in het tweetallig stelsel € 11111111 voor neerleggen.

We maken nu de berekening 111001 + 11101 (tweetallig)

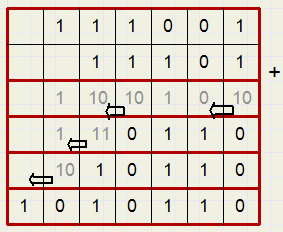
De tijdelijke uitkomsten zijn in grijs weergegeven.

Een voorbeeld van een vermenigvuldiging geef ik hier niet.
Aan het goede begrip voegt dat namelijk niet veel toe.
Interessanter is de uitleg hoe computers berekeningen maken, wellicht iets voor een volgend artikel.

Het 16- tallig stelsel

Een ander woord voor 16-tallig is "hexadecimaal".
Hiervoor zagen we dat getallen geschreven in het 2-tallig stelsel al snel erg lang worden.
Maar dat is te verkorten door steeds groepjes van 4 bits samen te nemen.
Zo'n groepje telt van 0000 (0) tot en met 1111 (15) en kent dus 16 verschillende standen.
Nu doet zich een probleempje voor : we moeten een cijfer bedenken voor de standen boven de 9
( 10..11..12..13..14..15).
Die cijfers noemen we a...f, zodat een hexadecimaal tellertje de volgende standen doorloopt:

0 1 2 3 4 5 6 7 8 9 a b c d e f ....0 1 2 3 4 5.....enzovoorts. De hexadecimale (+) en (x) tabellen geef ik hier niet.
Op de basisschool hexadecimaal rekenen is niet aan te raden.
De tabellen hebben namelijk 16 x 16 = 256 vakjes, dat is ruim 2,5 maal zoveel als in ons 10-tallig stelsel.
In oude culturen schijnt men wel het 60-tallig stelsel te hebben gebruikt.
Daarin rekenen is dan alleen weggelegd voor grote geleerden.

Door terug te grijpen op de telwerken en tabellen van hiervoor is in elk talstelsel te rekenen.

Omrekenen van talstelsels

Van vreemd- naar 10-tallig stelsel

We nummeren de cijfers in een getal van rechts (0) naar links.
Neem bijvoorbeeld het decimale getal 2765, zie het plaatje hieronder:

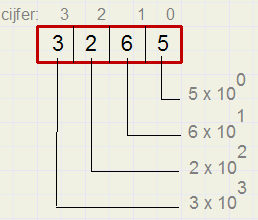
Merk op: elk getal tot de macht 0 is gelijk aan 1.In formule vorm: a⁰ = 1.

Dat is in te zien met de rekenregel a^p * a^q = a^p+q
Voor p = 0 staat er dan: a⁰ * a^q = a^q
a^q verandert niet door de vermenigvuldiging, dus we vermenigvuldigden met 1.

Nu rekenen we een binair getal naar het 10-tallig stelsel om:

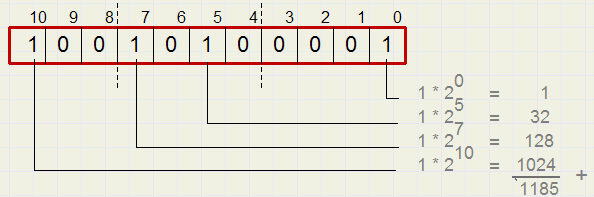
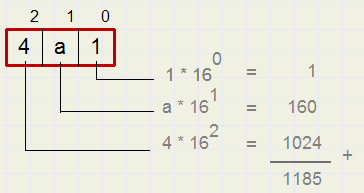
De omrekening kan sneller door 4 bits samen te nemen en van het hexadecimale getal uit te gaan:

Omrekenen naar een vreemd talstelsel

Als we een 0 plaatsen achter een getal in het 10-tallig stelsel, dat wordt dat getal 10 maal zo groot.
Dat is logisch als je bedenkt dat de cijfers 1 plaats naar links opschuiven, dus elk 10 maal zoveel waarde krijgen.
Schuiven we alle cijfers 1 plaats naar rechts, dan zijn we het meest rechtse cijfer kwijt en alle andere
krijgen een waarde die 10 maal kleiner is. Deze bewerking komt dus neer op delen door 10, waarbij
het meest rechtse cijfer als rest overblijft.

In het tweetallig stelsel verdubbelen we de waarde van een getal door er een 0 achter te zetten.
Schuiven we een binair getal 1 plaats naar rechts, dan delen we door 2 en het meest rechtse cijfer
is de rest van de deling.

Een tientallig cijfer herhaald door 2 delen en de resten opschrijven levert dus hetzelfde getal in het 2-tallig stelsel op.
We rekenen 1185 om naar het tweetallig stelsel:

 1185 : 2 = 592   rest 1
  592 : 2 = 296   rest 0
  296 : 2 = 148   rest 0
  148 : 2 =  74   rest 0
   74 : 2 =  37   rest 0
   37 : 2 =  18   rest 1
   18 : 2 =   9   rest 0
    9 : 2 =   4   rest 1
    4 : 2 =   2   rest 0
    2 : 2 =   1   rest 0
    1 : 2 =   0   rest 1

De resten van rechts naar links genoteerd levert : 1 0 0 1 0 1 0 0 0 0 1

We kunnen ook naar het 16-tallig stelsel omrekenen:

    1185 : 16 = 74 rest 1
      74 : 16 =  4 rest 10     {= a 16-tallig}
       4 : 16 =  0 rest 4

Zodat het antwoord luidt: 4 a 1

Gebruik van de rekenmachine bij omrekenen naar vreemd talstelsel

We rekenen het getal 97531 om naar het 8 tallig stelsel.

97531 : 8 = 12191,375   onthoud 12191 en bereken 0,375 * 8 = 3
12191 : 8 =  1523,875   onthoud 1523 en bereken 0,875 * 8 = 7
 1523 : 8 =   190,375   onthoud 190 en bereken 0,375 * 8 = 3
  190 : 8 =    23,75    onthoud 23 en bereken 0,75 * 8 = 6
   23 : 8 =     2,875   onthoud 2 en bereken 0,875 * 8 = 7
    2 : 8 =     0,25    bereken 0,25 * 8 = 2

Het antwoord is 276373

Opmerkingen

1.
Turven betitelt men wel eens als rekenen in het 1 tallig stelsel.
Maar mij dunkt dat het eerder rekenen in het "oneindig tallig" stelsel is.
Er moet immers voor elke hoeveelheid streepjes een andere naam worden bedacht!

2.
Een tientallig getal (of telwerk) van n cijfers heeft 10ⁿ standen, van 0....0 tot 9......9.
Een binair getal van n cijfers heeft 2ⁿ standen, van 0.....0 to 1......1

Een telwerk van n cijfers in het t tallig stelsel heeft tⁿ standen, van 0....0 tot (t-1)(t-1).....(t-1)

3.
Hieronder zie je een eenvoudig schema van een computer.

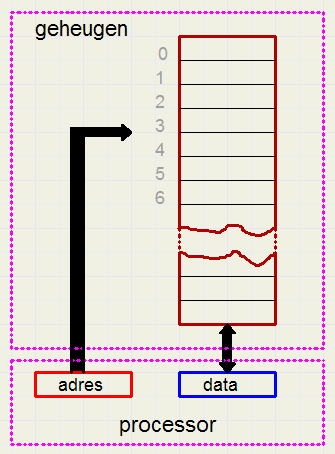
Het geheugen bestaat uit een groot aantal vakjes waarin een getal kan worden opgeslagen of uitgelezen.
Welk vakje dat is bepaalt het adres.
Voor communicatie met het geheugen heeft de processor de data bits (databus), de adres bits (adresbus)
en de signalen "lees" en "schrijf" (control bus). De controlbus is hier niet getekend.
De data in het geheugen bestaat uit instructies voor de processor, getallen, tekst of bytes die de kleur
van pixels aangeven.

De grootte van een computergeheugen, dus het aantal vakjes, is altijd een macht van 2.
Dat komt omdat het adres tweetallig is.
Aanvankelijk hadden computers een 20-bits adresbus.
2²⁰ = 1048576, wat in de winkel 1 megabyte werd genoemd.
Met een 20-bits adres kan je ruim één miljoen bytes adresseren.

De breedte van de databus is meestal een veelvoud van het aantal bits voor een teken.
Vroeger werden tekens (A,B,C...+ = - 9 $ enz.) in de BCD code weergegeven en die is 6 bits lang.
In zo'n code zijn dus 2⁶ = 64 verschillende tekens onder te brengen.
Computers in die dagen hadden een databus van 12, 24, 48 of 60 bits.
later kwam de ASCII code van 8 bits in zwang, zodat de databus een breedte kreeg die een veelvoud
was van 8.

De eerste PC's hadden een databus van maar één byte.
Latere computers konden 2 bytes tegelijk lezen en schrijven : een 16 bits databus.
De databus van de huidige Pentium machines is 32 bits, evenals de adresbus.
De maximale geheugengrootte is dus 2³² = 4.294.967.296 bytes (4 gigabyte)

Voor het rekenen met kommagetallen zij twee formaten in gebruik: 32- en 64 bits.
(4 - en 8 bytes)
4.
wat vind je van deze opmerking: "elk talstelsel is 10-tallig" ?

Wiskundige notatie

Tot slot van dit artikel gaan we het voorafgaande wat exacter opschrijven.
Het betreft hier basiskennis van talstelsels en coderen. Bij het schrijven van computerprogramma's
en daarbij vooral spelletjes en grafische programma's is dit van groot nut.

Terug naar de tellertjes uit het begin van dit artikel.
Het aantal standen van een teller noemen we de "modulus".
Een teller die 0...9..0...9 telt heet een "modulo 10" teller.
Stel dat zo'n modulo-10 teller de stand 5 heeft. Hoeveel maal is de teller dan opgehoogd?
Dat kan zijn 5, 15, 25,.......in het algemeen 10q + 5 maal waarbij q = 1,2,3.....
De stand is dus de rest bij deling door 10.
Die restberekening geven we aan met de operator mod (bekende operatoren zijn + , - , * , /)
Nu de notatie:

N mod m

Daarbij is de teller een aantal malen "over de kop" gegaan.
Een modulo-10 teller die 85 maal is opgehoogd is 8 maal over de kop gegaan
(heeft 8 maal een carry signaal afgegeven)
Stel dat we een modulo-m teller N maal ophogen.
N = mq + r.
Oftewel: N gedeeld door m heeft een quotient van q en de rest van de deling is r.
q is dan het aantal carries.
Zo'n deling met rest geven we aan met de operator div

N div m

Omrekenen van getal N naar een ander talstelsel m komt dus neer op:

Coderen

Een code is een getal (of reeks letters en cijfers) waarbij een verhaal hoort.
Voorbeelden van codes zijn: pincode, tramlijn 3, ACII code in computer (bv A = 65).

Een pannenkoekenhuis heeft de volgende keuzes:

Een bestelling moet worden omgezet in een getal (= code).
Hiervoor maken we een teller voor elke keuze, waarbij we de tellerstand aan de keuze koppelen.

meel	grootte	beleg
0 : wit	0 : klein	0 : naturel
1 : bruin	1 : normaal	1 : naturel
	2 : groot	2 : banaan
		3 : ham
		4 : kaas
		5 : appelstroop
		6 : poedersuiker

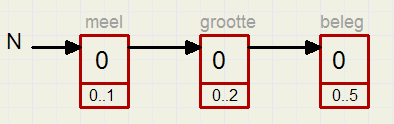
Bij tellerstand 000 hoort N = 0 en bestelling : wit, klein, naturel.

Iemand bestelt bruin, normaal, appelstroop. Welke code (N) levert dat op?
We beginnen met de hoogste (beleg) teller: die staat op 4, dus heeft 4 carries ontvangen van de vorige (grootte) teller.
De tellers "meel" en "grootte" samen vormen een modulo 2 * 3 = 6 teller.
Na elke 6 verhogingen staan ze weer op 00.
Voor stand 4 van "beleg" is dus een N = 4 * 6 = 24 nodig.

De "grootte" teller staat op 1, dat is 1 carry van de "meel" teller, die modulo 2 telt. Dus extra nodig N = 2.

De "meel" teller staat op 1, dus extra nodig N = 1.

De waarden van N opgeteld : 1 + 2 + 24 = 27. Dat is de code van deze bestelling.

Stel nu, dat de keuken de bestelling 27 ontvangt, welke pannenkoek moeten ze dan bereiden?
27 mod 2 = 1, dus de meelkeuze is 1 = bruin.
27 div 2 = 13.
13 mod 3 = 1. Dat is de code van de grootte, normaal.
13 div 3 = 4. Dat is de stand van de "beleg" teller, "appelstroop".

Programma

Lang geleden schreef ik in de programmeertaal Delphi een eenvoudig programma
om in verschillende talstelsels te tellen.
Hieronder staat een afbeelding:

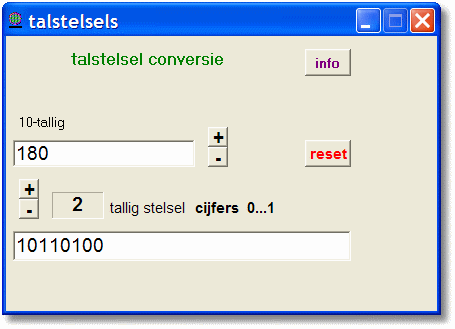
Het bovenste getal is steeds tientallig, het onderste staat in het 2 ... 16 tallig stelsel.
De getallen zijn steeds gelijk. Wordt de één veranderd dan past de andere zich aan.

Klik op het download icoontje (bliksem) bovenaan deze pagina om het programma te downloaden.