De Optimale Dakgoot

Luctor et Emergo
pompen of verzuipen
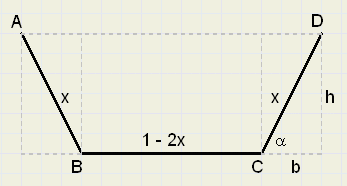Hieronder zie je de doorsnede van een (dak)goot.
Die doorsnede is een gelijkbenig trapezium.
De totale lengte van de de bekleding : AB + BC + CD = 1 (meter) en staat vast.

Variabel zijn de buigingshoek a en de lengte van de opstaande zijden x.

Vraag: voor welke waarden van a en x kan de goot zoveel mogelijk water bevatten of:
voor welke vorm is oppervlakte ABCD zo groot mogelijk?

Hieronder staan twee oplossingen:
    1. een grafische (met behulp van het programma Graphics-Explorer)
    2. een analytische (toepassing goniometrie en differentiaalrekening)

Een formule voor de oppervlakte
Zie de figuur hierboven:
De oppervlakte (A) bestaat uit een rechthoek (1-2x)h en twee driehoekjes, samen bh, zodat:
    A = (1 - 2x)h + bh
Nu is:
    h = x.sin(a)
    b = x.cos(a)
zodat
    A = x2.sin(a).cos(a) + (1 - 2x).x.sin(a)
    A = x2.sin(a).cos(a) + x.sin(a) - 2x2.sin(a)
Grafisch
Graphics-Explorer werkt met de variabelen x en y.
Bovendien kunnen in formules constanten (a,b,c) worden gebruikt.
Die constanten zijn met een muisklik van waarde te veranderen, waarbij de grafieken zich
automatisch aanpassen.
Het ligt voor de hand x te gebruiken voor de opstaande zijden, y voor de oppervlakte
en a voor de hoek a.

We tikken de formule in:
    y = x^2*sin(a)*cos(a) + x*sin(a) - 2x^2*sin(a)
en wijzigen de volgende instelling van Graphics-Explorer:
    - hoeken: graden ipv radialen
    - oorsprong (0,0) linksonder
    - +/- waarde voor wijziging constanten: 5 (graden)
    - zoom-middelpunt boven oorsprong
    - x- schaal (1) aan rechterkant (x wordt hoogstens 1)
    - y- schaal (0,2) boven
    - "Autoplot" (anders passen grafieken zich niet aan als constante wijzigt)
    - "Vervangen" (anders komen alle grafieken voor verschillende a's over elkaar)
Plot de formule en wijzig de waarde van a.
Bij de hoogste top van de grafiek kunnen we de waarden van x en a aflezen, zie figuur hieronder:
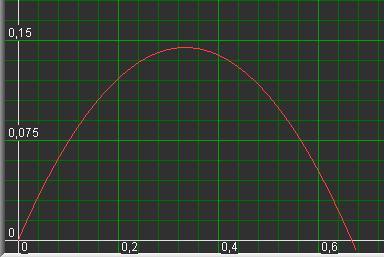Door de grafiek te maken voor verschillende waarden van a, merken we op dat de grootste oppervlakte
optreedt bij een hoek van ongeveer 60 graden, als x een derde deel van de totale lengte (1) is.

De Analytische benadering
Maxima en minima van functies zijn op te sporen door ze te differentiëren.
In een maximum of minimum zal de afgeleide gelijk 0 zijn.
De formule voor de oppervlakte heeft 2 variabelen, x en a,
zodat voor een maximum van A zowel de afgeleide naar x als naar a gelijk aan 0
zal moeten zijn.

A differentiëren naar x
    d A
    d x
     = 2 x ·  sin a ·  cos a +  sin a − 4 x ·  sin a = 0
    2 x ·  cos a + 1 − 4 x = 0
    2 x ·  cos a = 4 x − 1
    cos a = 
    4 x − 1
    2 x
A differentiëren naar a
    d A
    d a
     = x 2 (( cos a) 2 − ( sin a) 2) + x ·  cos a − 2 x 2 ·  cos a = 0
    x 2 ( cos a) 2 − x 2 ( sin a) 2 + x ·  cos a − 2 x 2 ·  cos a = 0
    x ( cos a) 2 − x ( sin a) 2 +  cos a − 2 x ·  cos a = 0
    x ( cos a) 2 − x + x ( cos a) 2 +  cos a − 2 x ·  cos a = 0
    2 x ( cos a) 2 + (1 − 2 x) ·  cos a − x = 0
Nu de eerder gevonden waarde van cos(a) invullen:
    2 x 
    2
    æ
    4 x − 1
    2 x
    		ö
    ­­
    èø
     + 
    (1 − 2 x) (4 x − 1)
    2 x
     − x = 0
    (4 x − 1) 2 + (1 − 2 x) (4 x − 1) − 2 x 2 = 0
    16 x 2 − 8 x + 1 + 4 x − 1 − 8 x 2 + 2 x − 2 x 2 = 0
    6 x 2 − 2 x = 0
    x = 
    1
    3
Tot slot x gebruiken om de beste waarde van a te vinden:
     
    cos a
         		 
     = 
     
    4
    3
     − 1
    2
    3
    		 
     = 
         		 
    1
    2

     
Zodat a = 60 graden.

De optimale dakgoot heeft zijden die een hoek van 60 graden maken met de bodem en
bodem en opstaande zijden zijn alle drie even lang.