

 |
In- en Omgeschreven cirkels |  |
 |
Inleiding
Meetkundige figuren met lijnen en cirkels vertonen allerlei merkwaardige eigenschappen.
Hieronder, in figuur 1, zie je getekend de driehoek ABC met ingeschreven- en
omgeschreven cirkel.
M is het middelpunt van de omgeschreven cirkel,
I is het middelpunt van de ingeschreven cirkel.
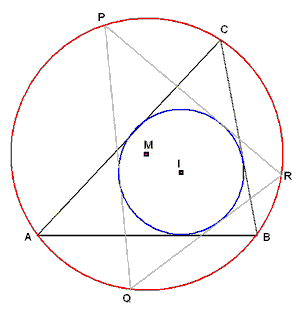 |
| fig.1 |
Vanuit P wordt een raaklijn getrokken aan de ingeschreven cirkel, die de
omgeschreven cirkel snijdt in Q.
Vanuit Q wordt weer een raaklijn getrokken....
Resultaat: het lijkt erop, dat de cirkels ook in- en omgeschreven cirkel
zijn van driehoek PQR.
We onderzoeken of dat juist is, of er oneindig veel driehoeken bestaan met de
gegeven in- en omgeschreven cirkels.
Als de cirkels ten opzichte van elkaar worden verschoven dan is te zien dat
er niet steeds een driehoek is te maken die de cirkels als in- en omgeschreven
cirkel heeft.(Neem bijvoorbeeld het geval waar de cirkels elkaar raken)
De onderlinge ligging van de cirkels wordt verder geheel bepaald door drie dingen:
-
1. de straal R van de omgeschreven cirkel
2. de straal r van de ingeschreven cirkel
3. de afstand MI
Als in deze formule alleen de variabelen R en r voorkomen, dan zijn er oneindig
veel driehoeken te tekenen.
Komt er een lengte van een zijde van de driehoek in voor, dan is het aantal
driehoeken beperkt.
op zoek dus naar een formule voor de afstand MI.
Tot mijn verrassing bleek dit probleem nog vrij lastig.
Benodigde voorkennis
-
1. basiskennis vlakke meetkunde
2. hoeken meten met cirkelbogen
3. macht van een punt t.o.v. een cirkel, hierna te behandelen
Het middelpunt van de ingeschreven cirkel is het snijpunt van de deellijnen
van de hoeken.
Het middelpunt van de omgeschreven cirkel is het snijpunt van de middelloodlijnen
van de zijden.
In een driehoek liggen tegenover gelijke hoeken gelijke zijden (en omgekeerd).
-2-
Zie artikel "de stelling van Thales"
-3-
Bekijk eens figuur 2.
Hierin is M het middelpunt van de cirkel en P is een willekeurig punt
binnen die cirkel en de straal is R.
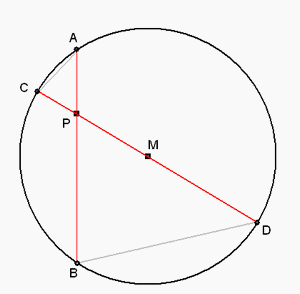 |
| fig.2 |
Immers:
-
- LA = LD = 0.5*boogBC
- LB = LC = 0.5*boogAD
Uit deze gelijkvormigheid volgt:
-
PA : PC = PD: PB, dus
PA.PB = PC.PD
nu is PC = R - PM en PD = R + PM zodat
PA.PB = (R - PM)(R + PM)
PA.PB = R2 - PM2
cirkel en P.
PA.PB heet de "macht" van P t.o.v. de cirkel.
opmerking:
Als P op de cirkel ligt, dan is de macht gelijk aan 0.
De formule voor de macht van een punt geldt ook als P buiten de cirkel ligt.
De gehanteerde formule is : PA.PB = PM2 - R2, en in dat geval
is de macht van een punt binnen de cirkel negatief en erbuiten positief.
Een formule voor de afstand MI
Zie figuur 3. hieronder:
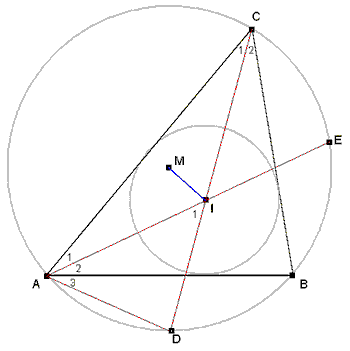 |
| fig.3 |
-
LC1 = LC2....dus boogAD = boogDB
LA1 = LA2....dus boogBE = boogCE
LA23 = 0.5*boogDB + 0.5*boogBE .... dus ook {zie boven}
LA23 = 0.5*boogAD + 0.5*boogCE
ook geldt: {Thales}
LI1 = 0.5boogAD + 0.5boogCE .....en dus
LI1 = LA23 ....dus
DA= DI
-
IC.ID = R2 - IM2
of
IM2 = R2 - IC.ID
en omdat ID = AD:
IM2 = R2 - IC.AD
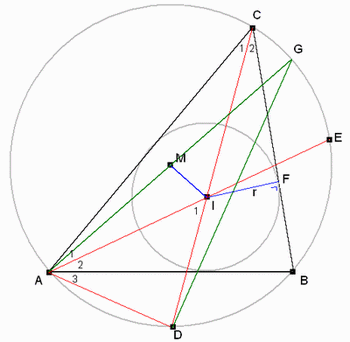 |
| fig.4 |
-
Straal r = IF staat loodrecht op BC
LCDA = 90o, want staat op de halve cirkelboog.
LG = LC1, want staan beide op boog AD.
Daaruit volgt:
-
IC : IF = AG : AD....of
IC : r = 2R : AD....waaruit volgt:
IC.AD = 2R.r
-
IM2 = R2 - IC.AD
-
IM2 = R2 - 2Rr
In de gevonden formule komen alleen de straal van de cirkels en de afstand
van hun middelpunten voor.
Er zijn dus oneindig veel driehoeken te tekenen die de gegeven cirkels als
in- en omgeschreven cirkel hebben.
Geldt de formule voor IM niet, dan is er geen enkele driehoek te vinden voor
een gegeven paar cirkels.
(Oeps, dat viel nog niet mee :-)
Naschrift
De formule voor IM is dermate simpel, dat het bestaan van een eenvoudiger afleiding
voor de hand ligt.
Zo kan worden geschreven:
-
IM2 + r2 = R2 - 2Rr + r2....of
IM2 + r2 = (R - r)2
Theorie ontleend aan:
"Leerboek der Vlakke Meetkunde", door Dr. P.Molenbroek.
(tiende druk, 1948).
Dit prachtige boek is in tweede-hands boekhandels soms aan te treffen.


