 |
 |
Opgaven algebra - 2 |
De antwoorden staan onderaan deze pagina
Herhaling
x = 3.....y= -2, bereken
1.
a. 100 - 5x + y2
b. 25 - x2 - y2
c. 20(x - y) - (x2 + 5y2)
d.
schrijf als één breuk, vereenvoudig zo mogelijk
laat haakjes staan in de noemer
e. +
f. +
g. +
h.
i.
j. voor een examen slaagt p% de eerste keer en 60% bij de herkansing.
Totaal is 80% geslaagd.
Bereken p.
 Platte Formules
Platte Formules
2.
schrijf als "platte" formule, op één regel
a. (x 2 + y 2) 3
b.
c.
 Afkappen en Afronden
Afkappen en Afronden
3.
kap af op honderden
a. 1798
b. 3999
kap af op tienden
c. 10,05
d. 10,88
rond af op duizenden
e. 173415
f. 99689
rond af op honderdsten
g. 0,12345
h. 1,075
rond af op 36 tallen
i. 123456
j. 395
 Functies
Functies
4.
f(x) = 2x - 7.........g(x) = -x + 8
bereken
a. f(0)
b. f(-5)
c. f(2k + 7)
d. f(x) + g(x)
e. f(g(x))
f. g(f(x))
g. f -1(x)
bereken k(x) als
h. f(k(x)) = 5x + 3
i. k(f(x)) = 5x +3
j. bereken m -1(x) als m(x) =
 Verhoudingen
Verhoudingen
5.
Hieronder staat een verhoudingstabel.
| x | 4 | 18 | 58 | ...... | 0,175 |
| y | 7,4 | 33,3 | 103,6 | 135,05 | ...... |
a. in de bovenste regel is 1 getal fout. Welk?
b. welk verband bestaat tussen x en y
c. bereken de open velden
De bewoners van Univeen hebben alleen auto's van het merk Ford en Opel,
in de verhouding Ford : Opel = 7 : 11.
d. hoeveel % van de auto's is een Opel?
Er zijn 492 meer Opels dan Fords.
e. Hoeveel van elke soort?
Een cirkelsegment is 42% van de oppervlakte van de hele cirkel.
f. welke middelpuntshoek heeft dat segment?
Bij een test vuurt men gelijktijdig twee raketten af naar een 70km. verder gelegen doel.
De snelheden van de raketten verhouden zich als 5 : 7.
g. bereken de snelheid van elke raket als de explosies 30 seconden na elkaar plaatsvinden.
 Gelijkvormigheid
Gelijkvormigheid
6.
D ABC ~ D PQR
AC = 18, BC = 30, QR = 40, PQ = 32
a. bereken AB
b. bereken PR
c. verdeel een lijnstuk van 17 cm. in 4 gelijke delen. Gebruik liniaal (zonder schaal) en passer.
Van twee driehoeken is bekend
- hun hoogtes verhouden zich als 2 : 5
- hun bases verhouden zich als 3 : 4
d. bereken de verhouding van hun oppervlakten
Zie de figuur hierboven, AB||DE
e. bereken DE
f. bereken CD
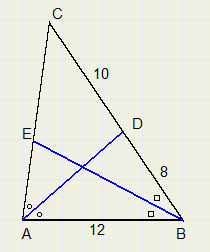
Zie de figuur hierboven, BE en AD zijn deellijnen
g. bereken AE en CE.
 Vergelijkingen
Vergelijkingen
7.
los de volgende stelsels vergelijkingen op
a. .........3x + 2y = -29
............2x + 5y = 34
b. .........7p - 10q = -64
............15p + 2q = -20
c..........v + 2w + 3x = 77
...........3v + 2w + x = 67
...........5v - w + 2x = 69
Consument A koopt 3 zakken kattenvoer en 5 blikken ham voor € 49,-
Consument B koopt 5 zakken kattenvoer en 3 blikken ham voor € 55,-
d. bereken de prijs van kattenvoer en ham.
Een fabriek maakt onderdelen A en B.
Onderdeel A bevat 2kg. ijzer en 1,4 kg. koper.
Onderdeel B bevat 2,5 kg. ijzer en 1,5 kg. koper.
In een jaar wordt 1950kg. ijzer en 1240kg. koper verbruikt.
e. hoeveel van elk onderdeel werd dat jaar geproduceerd?
 Wortels
Wortels
vereenvoudig (zo klein mogelijk getal onder wortelteken, geen wortel uit breuken,
geen wortels in noemer)
8.
a. 3 + 8 =
b. − 2 =
c. =
d. =
e. 3 =
f. 5 + =
g. 2 + 5 =
h. =
i. =
j. =
k. =
l. =
m. =
 Haakjes
Haakjes
9.
schrijf zonder haakjes, schrijf direct het antwoord op, zonder de termen te vermenigvuldigen
a. (x + 5)2 =
b. (2x - 1)2 =
c. (y - 5)(y + 5) =
d. (3k - 2m)(3k + 2m) =
e. (5x2 - 3)(5x2 + 3) =
f. (3y2 - 5)2 =
zie figuur hierboven
g. bereken BC
h. bereken DF
i. bereken de oppervlakte van driehoek GHI
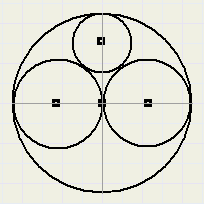
Zie de figuur hierboven.
Gegeven zijn 4 elkaar rakende cirkels met middelpunten.
De straal van de grootste cirkel is 1.
j. bereken de straal van de andere cirkels
schrijf zonder haakjes, vereenvoudig zo mogelijk
k. (x + y + z)(x - y - z) =
l. (3k + 5m)(2k - 3m - 2) =
m. =
n. (a + 1)3 =
 Ontbinden in Factoren
Ontbinden in Factoren
10.
schrijf als product van factoren
(factoren buiten haakjes halen)
a. x2 + 2x =
b. x3y6 + x2y4 =
c. 15x7 + 10x6 =
(kwadraat - kwadraat)
d. k2 - 25 =
e. 36p2 - 49 =
f. 25m4 - k6 =
g. 3x4 - 3 =
h. my4 - 9m =
(kwadraat, dubbelproduct, kwadraat)
i. y2 + 2y + 1 =
j. 4x2+ 20x + 25 =
k. k2 - 6k + 9 =
l. 36m2 -12m +1 =
m. 5x2 + 10x + 5 =
n. 3x3 + 30x2 + 75x =
o. (k + m)2 + 2k + 2m + 1 =
(som, product)
p. x2 + 7x + 12 =
q. x2 - x - 12 =
r. x4 - 2x2 - 15 =
s. 2p2 -22p + 36 =
t. x3 + 11x2 + 24x =
u. 3x5 - 15x3 + 12x =
v. (x2 + 6x + 9)2 - (x2 + 4x + 4)2 =
In de figuur hierboven staan 3 cirkels, die elkaar en een lijn raken.
Gegeven zijn de straal r en R
w. vind een formule voor straal x van de kleine, ingeklemde, cirkel.....x = ...r...R...
vereenvoudig zoveel mogelijk
 x. =
x. =
y. =
Antwoorden
1.
a. 81 b. 12 c. c. 71 d. 1/11 e.
f. | 3 m 2 + 2 m n + 5 n 2 |
| (m + n) (m − n) |
g. | x 2 + y 2 |
| (y − 3 x) (x + 3 y) |
h.
i.
j. 50%
2.
a. (x^2 + y^2)^3 b. (x+7)/(y+2) c. (1/x + (1/y + 5)^3)/((3x - 2)/(y - 4) + 1)^2
3.
a. 1700 b. 3900 c. 10,0 d. 10,8 e. 17300 f. 100000 g. 0,12 h. 1,08 i. 123444 j. 396
4.
a. -7 b. -17 c. 4k+7 d. x+1 e. -2x+9 f. -2x+15 g.
h. 2,5x + 5 i. 2,5x+20,5 j.
5.
a. 58 fout, 56 goed b. y = 1,85x c. 73.....0,32375 d. 38,89% e. 861 Ford...1353 Opel f. 151,2 g. 2743....3840
6.
a. 24 b. 24 c. -- d. 3:10 e. 8 f. 12 g. 6....9...
7.
a. x=7...y=4 b. p=-2...q=5 c. v=10...w=11...x=15 d. k=8...h=5 e. a=350...b=500
8.
a. 11
b. −
c. 3 d. 250 e. 12
f. 25
g. 26
h.
i. 4
j.
k.
l. 2
m. 6
9.
a. x2+10x+25 b. 4x2-4x+1 c. y2-25 d. 9k2-4m2
e. 25x4- 9 f. 9y4-30y2+25 g. 25
h. 24 i. 271,2 j. 1/2 ....1/3...k. x2-y2-z2-2yz l. 6k2+km-6k-10m-15m
m. | 6 x 2 + 4 x |
| (x + 2) (x + 1) |
n. a3+ 3a2+3a + 1
10.
 a. x(x+2) b. x2y4(xy2+1) c. 5x6(3x=2) d. (k-5)(k+5) e. (6p-7)(6p+7)
f. (5m2-k3) (5m2+k3)
a. x(x+2) b. x2y4(xy2+1) c. 5x6(3x=2) d. (k-5)(k+5) e. (6p-7)(6p+7)
f. (5m2-k3) (5m2+k3)
g. 3(x+1)(x-1)x2+1) h. m(y2-3)(y2+3) i. (y+1)2 j. (2x+5)2
k. (k-3)2 l.(6m-1)2 m. 5(x+1)2 n. 3x(x+5)2 o. (k+m+1)2
p. (x+3)(x+4) q. (x+3)(x-4) r. (x2+3)(x2-5) s. 2(p-9)(p-2) t. x(x+3)(x=8) u. 3x(x-1)(x+1)(x-2)(x+2)
v. (2x+5)(2x2+10x+13) w. x. a-b y. 2p




 Platte Formules
Platte Formules Afkappen en Afronden
Afkappen en Afronden Functies
Functies Verhoudingen
Verhoudingen Gelijkvormigheid
Gelijkvormigheid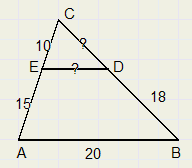
 Vergelijkingen
Vergelijkingen Wortels
Wortels Haakjes
Haakjes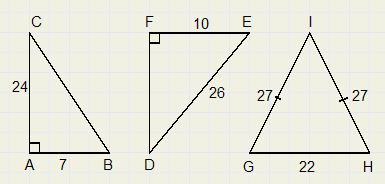
 Ontbinden in Factoren
Ontbinden in Factoren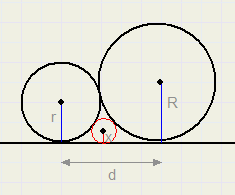
 x.
x.  a. x(x+2) b. x2y4(xy2+1) c. 5x6(3x=2) d. (k-5)(k+5) e. (6p-7)(6p+7)
f. (5m2-k3) (5m2+k3)
a. x(x+2) b. x2y4(xy2+1) c. 5x6(3x=2) d. (k-5)(k+5) e. (6p-7)(6p+7)
f. (5m2-k3) (5m2+k3)