Driehoeken en Zijden

Probleem
Gegeven zijn 3 lijnstukken met lengtes a, b en c.
Aan welke voorwaarde(n) dienen a,b en c te voldoen als ze de zijden vormen van een driehoek?

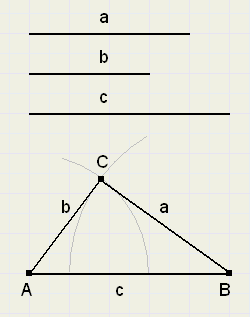
Bekijk figuur 1. hieronder, ontstaan door c als basis te nemen en vervolgens vanuit punt A
de lengte b om te cirkelen en daarna hetzelfde te doen voor lengte a vanuit punt B.

    fig.1

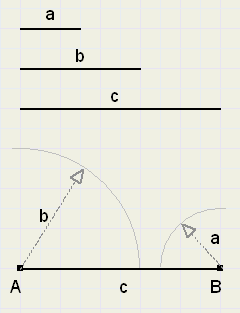
Bekijk nu figuur 2.
    fig.2

We zien, dat in figuur 1. wel een driehoek is te maken en in figuur 2. niet.
Ook de reden is duidelijk : in figuur 2. zijn a en b samen kleiner dan c.

De voorwaarde is dus te schrijven als de ongelijkheid :
    c < a + b
Uiteraard moet ook gelden :
    a < b + c .............en
    b < a + c
Aardig is het volgende:

Stellen we de halve omtrek van de driehoek s, dan is:
    a + b + c = 2s

    uitgaande van de ongelijkheid

    a < b + c...............kunnen we schrijven (links en rechts a bijtellen)
    2a < a + b + c
    2a < 2s.................dus
    a < s
Dit geldt natuurlijk ook voor b en c zodat de eis aan a,b en c ook geschreven mag worden als:
    elke zijde van een driehoek is kleiner dan de halve omtrek
Nog een aardig probleem
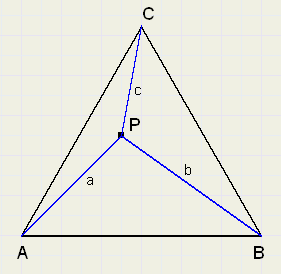
Gegeven is een gelijkzijdige driehoek met daarin een willekeurig gelegen punt P.
Vanuit P trekken we de lijnen PA = a, PB = b en PC = c.

Bewijs, dat a, b en c altijd een driehoek kunnen vormen.
Zie figuur 3 hieronder:
    fig.3

Oplossing 1.
Driehiek ABC is gelijkzijdig, stel de zijde heeft lengte z.
Dan geldt:
    a < z ...................en ook
    z < b + c
    ...........................combinerend:
    a < b + c
en op gelijke wijze:
    b < a + c
    c < a + b
Waarmee het bewijs rond is.

Oplossing 2.
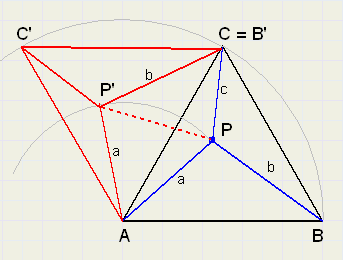
We roteren driehoek ABC 60 graden om het punt A.
B komt dus in C, C wordt C' en P wordt P'. zie figuur 4.
    fig.4

driehoek APP' is gelijkzijdig, want LP'AP is 60 graden en P'A = PA = a,
zodat LPP'A = LP'PA = 60 graden.
Dus PP'= a en we zien dat driehoek CPP' zijden a,b en c heeft.
Zeer verrassend.