Worteltrekken: iteratief en recursief

download root program
download Delphi-7 project

Inleiding

In dit artikel beschrijf ik programma's die de wortel uit een getal berekenen.
De programmeertaal is Delphi.
Klik op de bliksem icoontjes bovenaan om het programma of het hele project te downloaden.
Twee methodes komen aan de orde:
    1. een iteratieve
    2. een recursieve
Iteratieve procedures herhalen zichzelf een aantal malen.
Dat ziet er in het algemeen zo uit:



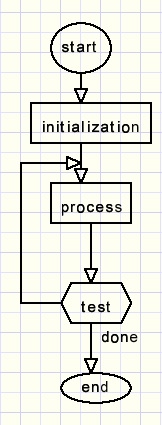
Initialisatie betreft een beginwaarde toekennen aan variabelen zoals
ook een telwerk dat het aantal herhalingen bepaalt.

Recursieve methodes roepen zichzelf aan.
Dat ziet er in het algemeen als volgt uit:



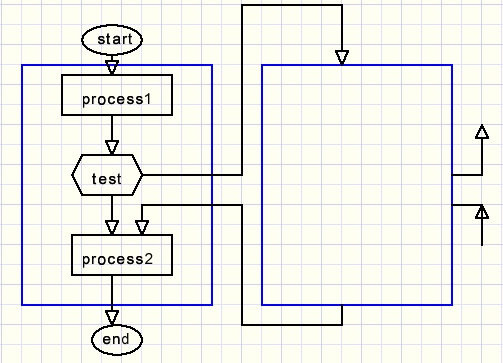
Proces1 wordt uitgevoerd, daarna volgt een test die uitwijst of de procedure zichzelf opnieuw aanroept.
Na de test volgt proces2.
Hierboven is dezefde procedure twee maal getekend voor de duidelijkheid.
Lokale variabelen en parameters in de procedure aanroep bevinden zich op het stack
en zijn dus per aanroep uniek.
Daarom is het handig om in gedachten net te doen of het verschillende procedures betreft.
Recursieve procedures zijn vaak zeer compact maar wel lastiger te begrijpen dan iterarieve.

Iteratief worteltrekken

Uitgegaan wordt van een 32 bit positief getal (maximum waarde 4294967295) dat we N noemen (number).
Het antwoord komt in varabele R (root) en verder is er nog register A (accumulator)
en S (subtractor), dat is de waarde die van A wordt afgetrokken.



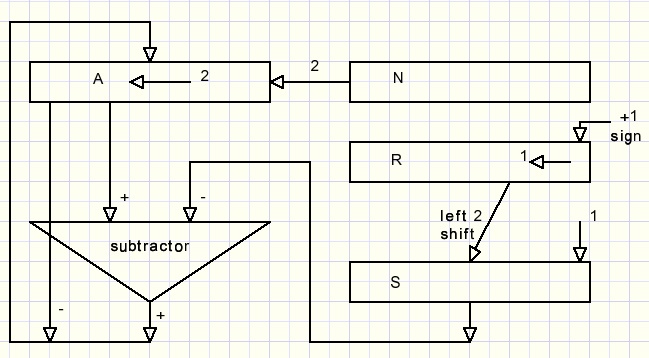
Dit zijn de stappen:
    1. register N is het getal waaruit de wortel wordt getrokken.
    2. A en R worden op 0 gezet.
    3. R 2 bits naar links geschoven + 1 gaat naar S.
    4. Registers A,N schuiven als één register 2 bits naar links.
    5. R schuift 1 bit naar links.
    6. Bepaal het teken van A - S.
    7. als positief: A = A - S, zet bit 0 van R op "1".
    8. herhaal stappen 3..7 (32 maal).
Na 16x twee bit shifts naar links is register N gelijk aan 0 geworden.
Het proces gaat daarna nog 16 stappen door maar nu dus achter de komma.
R bevat dan een integer waarde in bits 31..16 (dan de komma) gevolgd
door bits 15..0 achter de komma.
Er is een aparte procedure showRoot nodig om dit getal decimaal weer te geven.

Theorie

Stel we trekken de wortel uit een binair getal en hebben als partieel antwoord al a.
Nu zoeken we het volgende bit b, dat 0 of 1 kan zijn.
Het nieuwe antwoord is [ab]bits = 2a+b en het kwadraat (2a+b)2 = 4a2+4ab+b2.
Die 4a2 werd al eerder van het oorspronkelijke getal afgetrokken.
Te bepalen is dus bit b in de rest 4ab + b2 = b(4a + b) dus
voor b=1 moet S = (a shl 2) + 1 van de rest aftrekbaar zijn.
Dat levert een nieuwe waarde van R en een nieuwe rest waarna op dezelfde manier het volgende bit b wordt bepaald.
Bij decimaal worteltrekken met potlood en papier moet bij het begin S2 (0,1,4,9,..81) worden bepaald:
het grootste kwadraat dat aftrekbaar is.
Bij binaire getallen vervalt die stap.
R = 0 levert vanzelf S = 1 op.

Dit is de iteratieve procedure:
(variabelen A,N,S staan buiten de procedure en worden ook door het recursieve proces gebruikt) 
var A,N,S : dword;
.....
procedure TForm1.Button1Click(Sender: TObject);
//calculate root, iterative way
var i : byte;
    R : dword; //result register, point in center
begin
 try
  N := strtoint(edit1.Text);
 except
  N := 1;
  edit1.Text := '1';
 end;  
 R := 0;
 A := 0;    //accumulator
 for i := 1 to 32 do       //root process
  begin
   A := (A shl 2) or (N shr 30);
   N := N shl 2;
   S := (R shl 2) or 1;    //subtract value
   R := R shl 1;
   if S <= A then begin
                   A := A - S;
                   R := R or 1;
                  end;
  end;
 showroot(R);
end;
De procedure showRoot toont het antwoord.
Dat antwoord wordt gesplitst in delen voor en achter de komma.
Het getal achter de komma wordt steeds vermenigvuldigd met 10 waardoor
de decimale waarden er links van de komma uit "ploppen".
De bijgetelde waarde 5 dient voor de afronding.
De nauwkeurigheid achter de komma is maximaal 4 cijfers.
Zie de source code voor de details.

De recursieve methode

Eerst even wat theorie.
Bekend uit de algebra is deze ontbinding in factoren: a2-b2 = (a-b)(a+b).
Zodat ook:



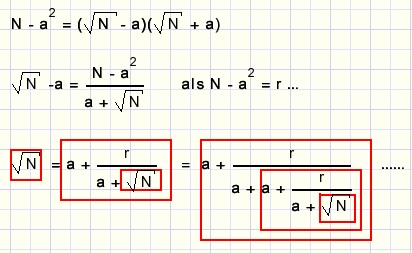
Hier zien we de recursie al zitten.
N is het getal waaruit we de wortel willen trekken.
a is het grootste getal waarvan N het kwadraat bevat.
r is de rest N - a2.
Deze waarden veranderen niet tijdens het proces van worteltrekken.
Hoe dieper we in de noemers afdalen hoe kleiner de invloed,
zodat de wortel met elke stap in nauwkeurigheid toeneemt.

Eerst moeten dus a en r worden bepaald, daarna kan het recursieve proces beginnen.
Het antwoord komt in variabele root. 
procedure TForm1.Button2Click(Sender: TObject);
//calculate root recursive way
var i,c  : byte;
    root : double;
begin
 try
  N := strtoint(edit1.text);
 except
  N := 1;
  edit1.Text := '1';
 end;
 c := 0;      //shift count
 if N > 0 then
  begin
   for i := 0 to 31 do                   //vind hoogste -1- bit
    if ((1 shl i) and N) <> 0 then c := i;
   c := c shr 1;                         //wortel
   A := 1 shl c;                         //largest single bit root
   S := N - (A shl c);                   //S - A*A
   root := RecROOT(10);                  //depth = 10
  end
  else root := 0;
 statictext2.Caption := FormatFloat('#0.0#####',root);
end;
En hier de recursieve functie: 
function RecROOT(i : byte) : double;
//recursive root, i is depth
begin
 if i >1 then result := A + S/(A + RecROOT(i-1))
  else result := A + S/(2*A);
end;
De enige parameter is de diepte om de recursie te beëindigen.
De functiewaarde is de wortel.
Hoe groter de diepte hoe nauwkeuriger het antwoord.

Zie de source code voor meer details.
Tenslotte nog een plaatje van het Delphi-7 project in actie: