| Wegennetten |  |
Hieronder tref je een systematische uitleg aan over wegennetten.
Wat is een wegennet en wat moet je er mee?
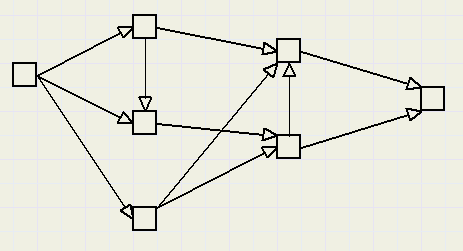
Een wegennet is een tekening van lijnen. Die lijnen beginnen en eindigen ergens.Dat begin en einde is hier als een vierkantje getekend, maar een punt mag ook.
Er is éénrichtingsverkeer.
De vraag is steeds hoeveel routes er zijn tussen twee punten.
Een wegennet is een abstracte weergave van een samengesteld proces.
Het kan een echte landkaart voorstellen met vertakkende wegen maar ook keuzes op
de menukaart in een restaurant.
Of een punt stelt een situatie voor, de lijnen zijn de processen die van de ene naar de andere toestand leiden.
Wegennetten hebben daarom ook veel te maken met combinatoriek, kansrekening en procesanalyse.
De hoofdregel bij wegennetten
Voor het bepalen van het aantal routes in een wegennet is er slechts één regel : de plusregelBekijk het stukje wegennet hieronder:
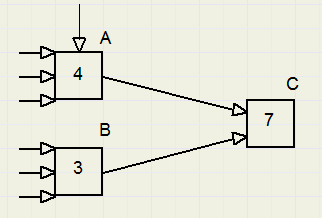
Dat is alles.
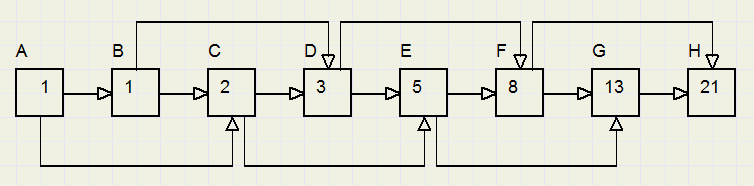
We berekenen het aantal routes van A naar G in het wegennet hieronder,
hetzelfde wegennet als bovenaan deze pagina
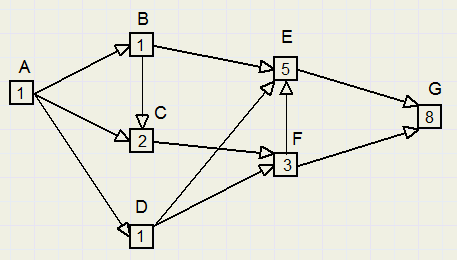
Daarom is de waarde 1, we kunnen er maar op één manier komen.
B heeft 1 binnenkomende weg vanaf A en krijgt dus dezelfde waarde als A: B=1
C heeft inkomende wegen van A en B, dus C = A + B = 1 + 1 = 2.
Enzovoorts.
Zo is E = B + D + F = 1 + 1 + 3 = 5
en G = E + F = 3 + 5 = 8
Speciale wegnnetten
Onafhankelijke keuzes : de vermenigvuldigregel
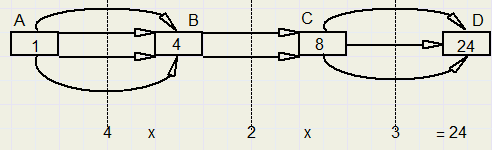
In C uit twee hoofdmenus en bij D is een keuze gemaakt uit 3 toetjes.
Er zijn in deze horecagelegenheid dus 4 x 2 x 3 = 24 menukeuzes mogelijk.
Het vermenigvuldigen van het aantal keuzes kan alleen, als een keuze onafhankelijk is van de voorgaande.
Alle punten worden steeds in dezelfde volgorde doorlopen.
Rechthoekige netten
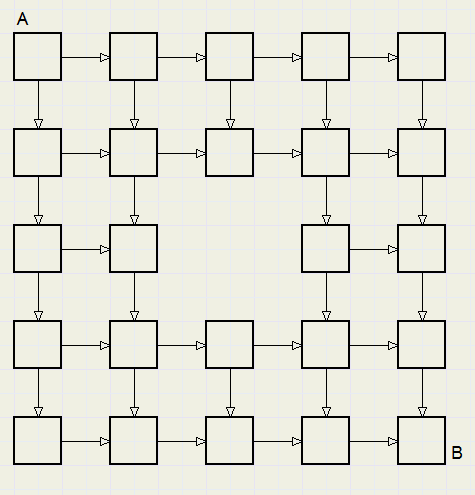
Hoeveel routes zijn er van A (links boven) naar B (rechts onder)?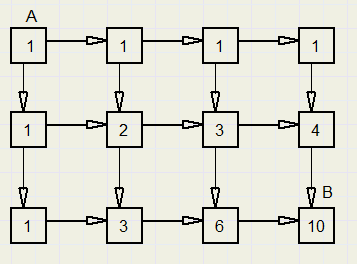
De punten aan de bovenrand en de linker zijrand hebben allemaal de waarde 1,
omdat er maar 1 weg met waarde 1 binnenkomt.
Inplaats van alle punten te turven kunnen we ook een formule invullen om het antwoord
direct te berekenen. Die theorie staat [hier].
Maar onze telmethode is flexibeler, want als er extra routes zijn of wegblokkades,
dan werkt de formule niet meer maar het turven wel.
Knikkerplanken of munten opgooien
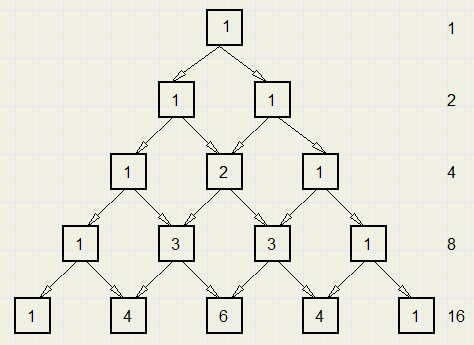
de knikker kan links of rechts passeren.
Opvallend is, dat de optelling van de routes in een regel een oplopende macht van 2 oplevert.
(1,2,4,8,16.....)
Maar bij nader inzien is dat wel logisch.
Per regel wordt er een keuze uit 2 wegen gemaakt: links of rechts.
Per regel verdubbelt het aantal keuzes.
Het totaal aantal keuzes is dus 2regels
De keuze linksom of rechtsom kan worden vervangen door kop (K) of munt (M).
Elk punt heeft een uitgaande weg K (links) en M (rechts).
De tweede regel is dan K...M
De derde regel: KK....KM/MK....MM
De derde regel: KKK....KKM/KMK/MKK....MMM
Er is ook overeenkomst met de algebra: formule (a + b)n
n = 1: 1.a + 1.b
n = 2: (a+b)(a+b) = aa + ab + ba + bb = 1.a2 + 2.ab + 1.b2
n= 3: (a+b)(a+b)(a+b) = aaa + aab + aba + baa + abb + bab + bba + bbb = 1.a3 + 3.a2b + 3.ab2 + 1.b3
Lees voor a KOP en voor b MUNT om de overeenkomst te zien.
Fibonacci of konijnenfokken
De Fibonacci reeks luidt: 1..1..2..3..5..8..13..21..Een nieuw getal is steeds de optelling van de twee vorige.
De associatie met konijnenfokken ontstaat door aan te nemen dat elk paar konijnen
elke maand een paar jongen krijgt en die jongen twee maanden nodig hebben om volwassen te worden
en ook weer jongen gaan werpen.
De konijnen gaan ook niet dood.
Dat is met een wegennet aan te geven:
Teken aparte vakjes voor volwassen dieren, pas geboren jongen en jongen van 1 maand oud.
Splits dan het wegennet uit, zodat op elk moment te zien is hoeveel konijnen er
van elke leeftijd (0,1 en > 1 maanden) zijn.
Opgave2:
Bepaal in het wegennet hieronder het aantal routes van A naar B.