Boomstructuren programmeren (versie 5)
bekijk Delphi source code van de Tree unit.
download Tree-exerciser programma.
download complete Delphi - 7 project

Introductie

In de wiskunde is een graaf een tekening met punten (ook wel nodes geheten), die wel of niet met lijnen zijn verbonden.
Een punt (node) stelt een situatie of een object voor.
Een verbindingslijn geeft een afhankelijkheid aan of een overgang van toestanden.
Grafentheorie gaat over de eigenschappen van grafen.
Grafen worden op verschillende terreinen toegepast zoals
  • wegennetten en plattegronden
  • elektrische netwerken
  • moleculen
  • industriële planning
  • combinatoriek
  • informatie technologie:
    • file systemen
    • computer games
    • text editing

Bomen

Een boom is een bepaald type graaf.
Eigenschappen van een boom-graaf zijn:
  • er zijn geen geïsoleerde nodes (elke node is minimaal met een andere verbonden)
  • als één verbindingslijn wordt verwijderd dan ontstaan 2 losse grafen.
  • de route van node A naar B is dezelfde als van B naar A, er zijn geen rondritten mogelijk.
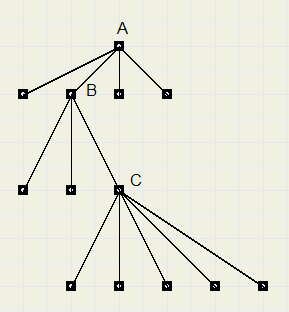
Hieronder staat een voorbeeld van een boom.
.

Die kan bijvoorbeeld een file systeem voorstellen waarin map A vier files bevat,
met oa map B met daarin drie files waaronder map C met weer vijf files.

Dit artikel gaat over het programmeren van boomstructuren.
Het omvat het creëren van bomen, het aanbrengen van wijzigingen en ook undo: wijzigingen ongedaan maken.
Het Delphi-7 project heeft drie units:
    1 : unit1
      - paintboxen om bomen zichtbaar te maken en edit akties weer te geven
      - knoppen voor het creëren en bewerken van de boom
    2 : data unit met data die door de programmeur is gedefinieerd
    3 : tree unit met data structuren om de boom weer te geven en proceduren en functies voor bewerkingen.
Alle code voor het wijzigen en ongedaan maken van wijzigingen staan in de tree unit.
Form1 en Unit1 maken het testen van de boom-procedures mogelijk.
Het enige doel van de aparte data unit is scheiding van inhoud en structuur van de boom.

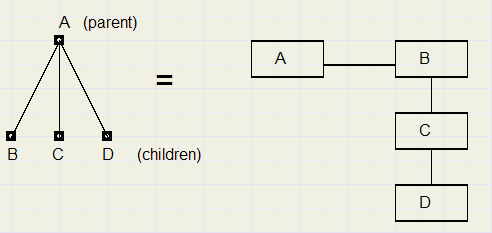
Hierboven staat een graaf met elementen A,B,C,D.
A wordt de parent genoemd. B,C,D zijn afstammelingen (children) van A.
B,C,D zijn op één of andere manier van A afhankelijk.

A kan een lijn zijn met tekst met daarin de tekens B, C en D.
Links staat de wiskundige notatie, rechts de ICT notatie, bekend van file systemen.

Data structuren

De boom wordt beschreven door een array, elke entry is een node.
Per node moeten verbindingen worden weergegeven als
    - parent : de ouder
    - child : het kind (afstammeling)
Nu ontstaat een probleem, want een ouder kan een hele ris kinderen hebben.
Het is onhandig om per node een groot array met al die kinderen in te voegen.
Handiger is om per node een eigenschap next toe te voegen, wijzend naar het volgende kind van de ouder.
Voor het gemak (om snel de weg terug te vinden) dan ook maar een eigenschap previous per node.

const maxelement = 50;

type TLinks  = record
                parent   : dword;
		     child    : dword;
		     next     : dword;
		     previous : dword;
		    end; 
		   
var Links : array[1..maxelement] of TLinks;
Dit is dus exclusief de data van de applicatie, die staat in een apart array.
Ter demonstratie is deze eenvoudige data gekozen, ook handig voor het tekenen van de graaf: 
type TElement = record
                 x : word;
                 y : word;
                end;	 
					
var Element : array[1..maxelement] of TElement;
In werkelijkheid zal de data veel uitgebreider zijn met codes, fonts, kleuren, scherm positie...
in het geval van een editor.

Elke node heft dus een nummer: zijn index in array's TLinks en TElement.

Dus, de verbindingen van node 23 staan in Links[23], de data staat in Element[23].

Het eerste en bovenste element van de boom is 1.
Deze node heeft geen parent of previous node, wat wordt aangegeven met de waarde 0.


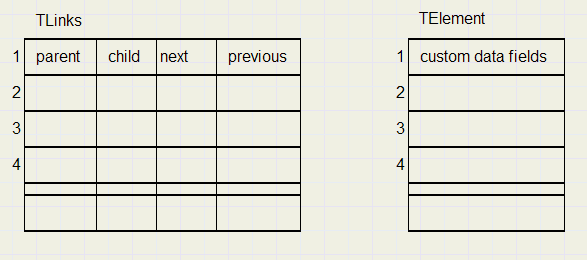
Hieronder staat een element (node) met zijn verbindingen :
Bekijk bijvoorbeeld de boom hieronder:
De exerciser tekent deze zo:
Element 1 heeft als children 2,3,4.
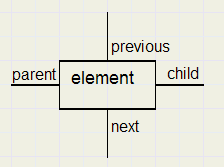
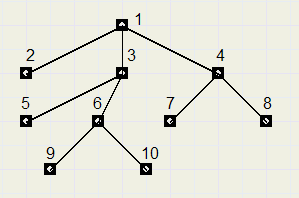
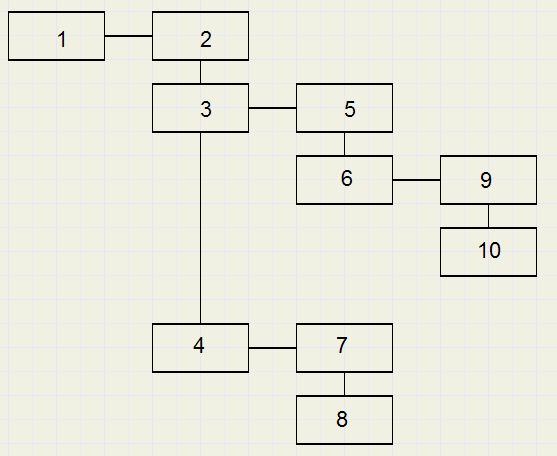
De parents van nodes 2,3,4 zijn allemaal 1.
Next van nodes 4,6,8,10 zijn 0.
Previous van nodes 1,2,5,7,9 zijn ook 0.

Toepassing in een wiskunde editor

Wiskunde editors zijn gecompliceerder dan gewone teksteditors wegens breuken, machten en speciale tekens als wortels.
Hieronder staat een breuk met teller en noemer als onderdeel van een lijn.

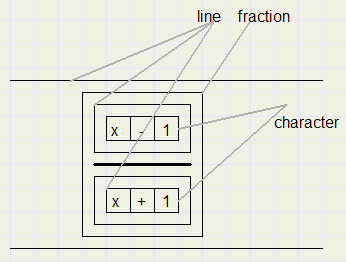
De tekstlijn is een element met als child een breuk-element.
De teller en noemer zijn lijnen en children van het breuken element.
De teller heeft drie children: de teken elementen met codes x, - , 1
De noemer (lijn) heeft children met de character codes x, +, 1.

De boomstructuur maakt automatisch uitlijnen mogelijk:
als de lengte van de teller verandert, dan kan de positie van de noemer worden aangepast.

De graaf hieronder geeft de breuk weer:

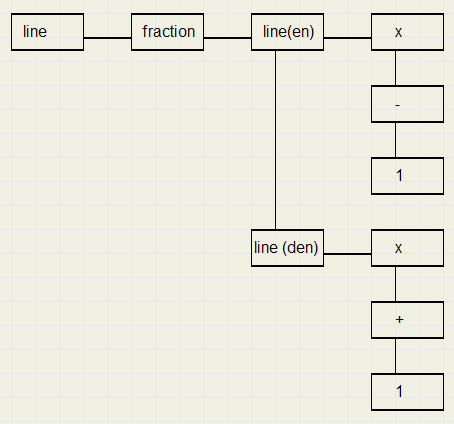
Bewerkingen op bomen

    Place afterplaats een nieuw element na een ander
    Place beforeplaats een nieuw element voor een ander
    Place Child afterplaats een nieuw element als laatste kind (voeg kind toe)
    Place Child beforeplaats een nieuw element als eerste kind
    Replacevervang een element door een nieuw
    Packmaak een element kind van een nieuwe parent
    UnPackverwijder de parent, voeg children in
    Deleteverwijder een element inclusief children
    Move afterplaats een bestaand element na een ander
    Move beforeplaats een bestaand element voor een ander
    Move Child afterplaats een bestaand element als laatste kind van een ander
    Move Child beforeplaats een bestaand element als eerste kind van een ander
    undomaak laatste bewerking ongedaan

Element status

De status van een element wordt opgeslagen in bits 24..31 van het parent field.
type  TElementStatus = (esFree,esActive,esDeleted,esReplaced,esUnpacked);
    esFreeelement is niet in gebruik
    esActiveelement is deel van de boom
    esDeletedelement is verwijderd, kan door undo weer oude plaats innemen
    esReplacedelement is vervangen door ander
    esUnpacked element is een verwijderde parent

mark

Markeren is geen boom-bewerking maar een functie van de exerciser.
De links van een gemarkeerd element worden linksonder op het form getoond.

Place after, Place before

procedure PlaceA(del,sel : dword);//plaats vrij element sel {selected element} na element del {destination element}
procedure PlaceB(del,sel : dword);//plaats vrij element sel achter del
Deze bewerkingen zorgen voor het toevoegen van elementen als letters en cijfers, tabellen, haakjes, breuken
of regels met tekst op een pagina.
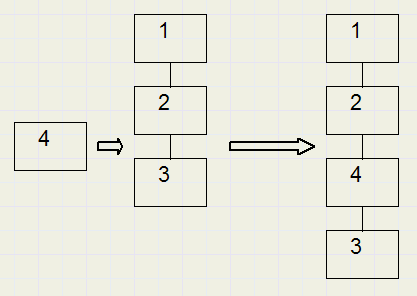
Place after: Element 4 is ingevoegd na element 2.
Place before: Element 4 is ingevoegd voor element 3.

Place Child after, place Child before

 procedure PlaceChildA(del,sel : dword);//plaats vrij element sel als laatste child van del
 procedure PlaceChildB(del,sel : dword);//plaats vrij element sel als eerste child van del
Deze bewerkingen voegen een nieuw child toe.
De nieuwe positie is eerste of laatste.
De bewerkingen zijn identiek als het element nog geen child heeft.
In het plaatje hieronder:
element 5 is ingevoegd als eerste kind van element 1.
element 5 is ingevoegd als eerste kind van element 1.

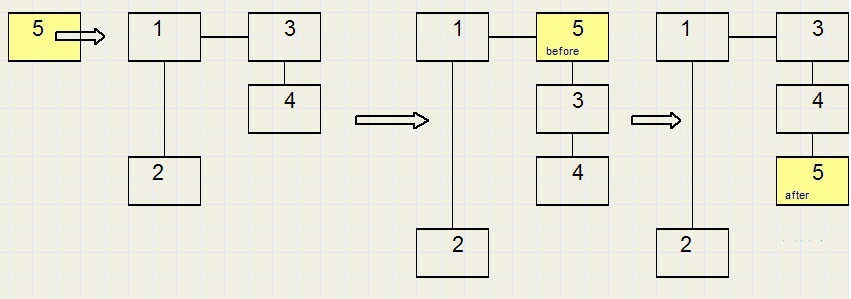
Move element after , before

procedure moveElA(del,sel : dword);//plaats actief element sel achter del
procedure moveElB(del,sel : dword);//plaats actief element sel voor del
Deze bewerking verwijdert een actief element en plaatst het voor of achter een ander actief element.

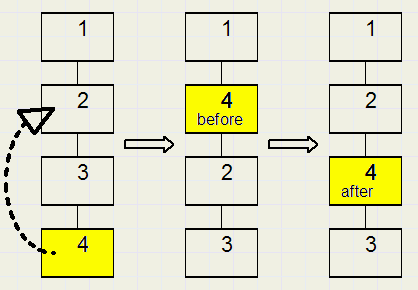
Replace

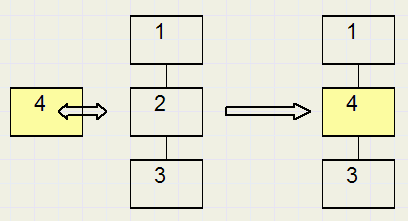
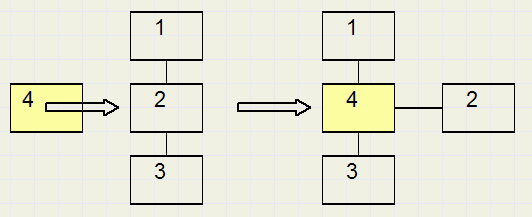
procedure ReplaceEL(del,sel : dword);//vervang actief element del door vrij element sel
vervang een element door een nieuw. Element 2 wordt vervangen door element 4.

Pack

procedure packEl(del,sel : dword);//vrij element sel wordt parent van actief element del
Maak een element het kind van een nieuw element.
Element 2 wordt kind van element 4

UnPack

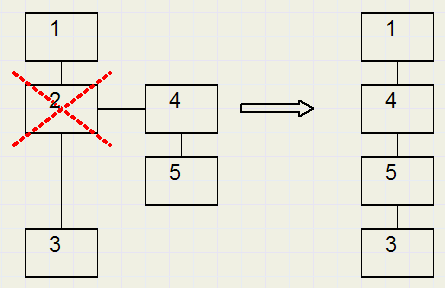
procedure unpackEl(sel : dword);//verwijder actief element sel, maar voeg kinderen in
Verwijder de parent.
Element 2 wordt verwijderd, maar niet de children.

Delete

procedure deleteEL(del : dword);//verwijder element del, inclusief children
Het geselecteerde element wordt uit de boom gehaald, evenals alle kinderen.

Gebruik van de exerciser



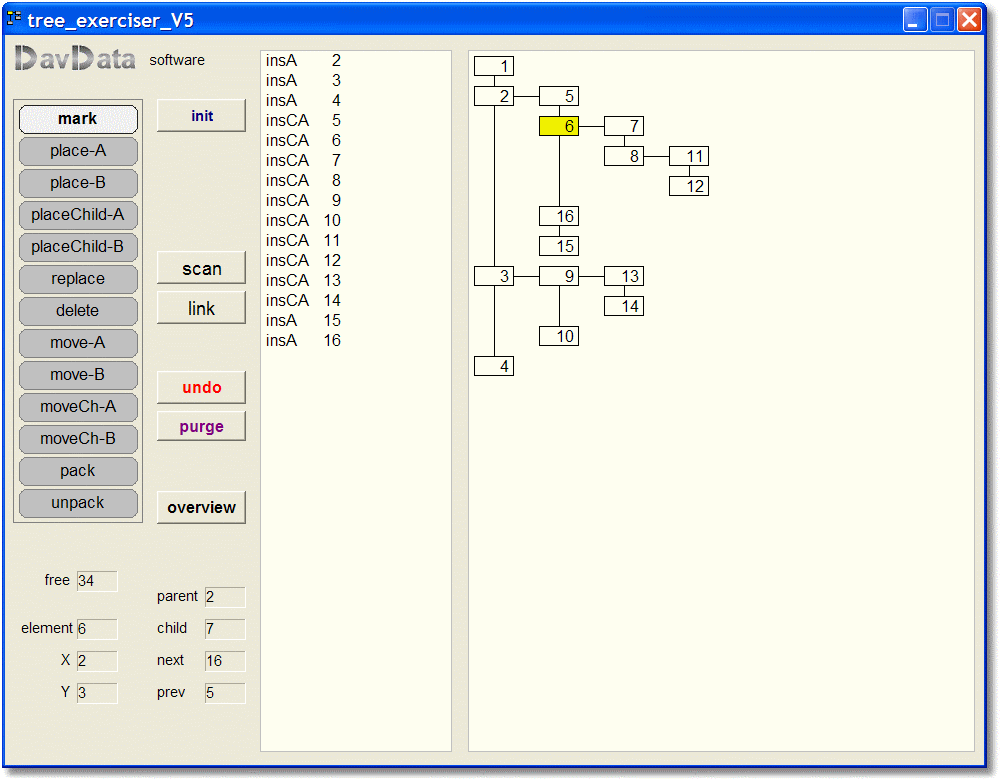
Voor de bewerkingen PlaceA, PlaceB, PlaceChildA, PlaceChildB, Replace, Pack, UnPack, Delete:
    Plaats muiswijzer op element en klik
Voor de bewerkingen moveA, moveB, moveChildA, moveChildB:
    Plaats muiswijzer op het element.
    Druk linkermuisknop in en houd ingedrukt.
    Verplaats muiswijzer naar ander element, plaats linkerbovenhoek van versleepte element binnen doel-element.
    Laat linkermuisknop los.

The Undo system

Een bewerking wordt opgeslagen in een geheugen met stack structuur en entries TEditaction: 
const maxUndo = 25;
....
type TLinkType      = (ltNone,ltParent,ltChild,ltNext,ltPrevious);
     TELaction      = (eaPlaceA,eaPlaceB,eaPlaceChildA,eaPlaceChildB,eaReplace,
                       eaDelete,eaMoveA,eaMoveB,eaMoveChildA,eaMoveChildB,
                       eaPack,eaUnpack,eaUndo,eaNone);
     TEditAction = record
                    action  : TELaction;
                    elmnt   : dword;     //element
                    linkEl  : dword;     //link element
                    linktype: TLinkType;
                    cc      : dword;     //child count
                    bwlink  : boolean;   //backward link
                   end;
.........
var startflag,linkflag : boolean;
    UndoStack : array[1..maxundo] of TEditAction;
De velden zijn:
    actiontype aktie
    elmntnummer van het element
    linkElnummer van element dat werd vervangen
    linkType type link, ltPrevious of ltParent
    cc aantal children in geval van een UnPack bewerking
    bwlink vlag die bewerking koppelt aan de vorige.
Deze informatie maakt mogelijk dat elke bewerking ongedaan gemaakt kan worden.
Constante maxUndo is het maximale aantal bewerkingen dat de stack onthoudt.

Om de laatste bewerking ongedaan te maken: 
procedure UndoAction;
Om alle opgeslagen bewerkingen in het Undo stack te wissen: 
procedure purgeUndoStack;
Om volgende bewerkingen te koppelen (zodat ze later gezamenlijk ongedaan gemaakt kunnen worden): 
procedure startLinking;
Koppeling van bewerkingen opheffen: 
procedure stoplinking;
Data in het undo-stack opvragen: 
function getstackdata(n : word) : TEditAction;

Linken

Een edit operatie kan bestaan uit verschillende basis bewerkingen op de boom.
Een undo moet dan slaan op al deze bewerkingen die bij elkaar horen.
Daartoe kan de bwlink (backward link) vlag worden aangezet, om bewerkingen in het Undo Stack te verbinden.

procedure startlinking zet de startflag aan en de linkflag uit.
procedure registerAction zet de undo informatie van een bewerking op het stack en kopieert de startflag naar de linkflag.
Volgende bewerkingen registreren nu met bwlink := linkflag, dus zijn met de vorige bewerking verbonden.
procedure stoplinking zet de startflag en de linkflag uit.

Destroying elements

Verwijderde of vervangen elementen worden nog steeds bewaard omdat een undo ze weer actief maakt.
Er is geen directe manier om elementen vrij te maken.
Echter, als het undo-stack vol is en nieuwe bewerkingen worden toegevoegd,
dan moet het stack opschuiven waarbij positie [1] wordt overschreven.
Als deze positie een verwijderd, vervangen of unpacked element bevat, dan is het daarna onmogelijk
om dit element weer actief te maken want de undo informatie bestaat niet meer.
Zo'n element wordt daarom vrij gemaakt, zodat het voor nieuwe bewerkingen kan worden ingezet.

Programmeren

Initialization

Bij de start moet de boom worden ingesteld met: 
procedure initTree;
Dit zet alle links op 0 en maakt Links[1] actief.

Links[1] mag nooit verwijderd worden, het is het startpunt (kruin) van de boom.

In the data unit: 
procedure initTreeData;
om alle velden op nul te zetten van het array Element[ ]

Nieuw toe te voegen elementen aan de boom moeten de status free hebben.
Om het nummer van een vrij element te krijgen:
function getFreeEl(var el : dword) : boolean;//levert nummer el van een vrij element
//return true als  Ok, false als er geen vrij element is

Navigatie

function ParentEl(var nel : dword) : boolean;
function ChildEl(var nel : dword) : boolean;
function NextEl(var nel : dword) : boolean;
function previousEl(var nel : dword) : boolean;
Het parent, child, next of previous element van nel wordt geretourneerd.
Als zo'n element er niet is, dan wordt nel niet gewijzigd en het resultaat is false.

function ScanElement(var elmnt : dword; lt : TLinkType) : TLinktype;
Uitgaande van element elmnt en zijn linktype lt wordt een nieuw element geleverd in elmnt.
Het doel is om stap voor stap door de boom te gaan op een systematische manier.
als:
    it = ltParent: zoek dan voor next, dan previous, dan parent
    it = ltChild of
    it = ltNext : zoek voor child, dan next, dan previous, dan parent
    it = ltPrevious: zoek voor previous, dan parent
De scanelement functie wordt gebruikt bij het tekenen van de boom.
Opvolgend aanroepen van deze functie adresseert eerst alle kinderen, dan next elementen, dan previous en parents.
Elk element wordt twee maal aangedaan: gedurende de heen- en de terugweg.
De protected procedure destroyELch gebruikt scanelement om een element inclusief kinderen te verwijderen.

Status

De links van en element opvragen: 
function GetElLinks(n : dword) : TElLinks;
De status van een element opvragen: 
function getELStatus(el : dword) : TElementStatus;
Het aantal kinderen van een element opvragen: 
function getChildCount(del : dword) : dword;
Het laatste kind van een element opvragen: 
function getLastChild(del : dword) : dword; //return 0 if no child
Het aantal vrije elementen, laatst toegewezen element en aantal undo bewerkingen in het stack opvragen: 
function getTreeStatistics : TTreestats;//return tree statistics

Undo

   procedure UndoAction;
Maakt de laatste bewerking ongedaan.
Toegevoegde elementen worden uit de boom gehaald en vrijgemaakt voor nieuw gebruik.
Verwijderde of vervangen elementen nemen hun oude plaats weer in.

Om alle undo informatie te wissen, wat herstel onmogelijk maakt: 
   procedure purgeUndoStack;
Dit is de manier om nieuwe vrije elementen te krijgen als er veel zijn verwijderd of vervangen.

Hiermee besluit ik de beschrijving van de boom structuren en de bewerkingen.
Voor meer details verwijs ik naar de source code.