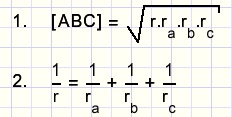de straal van in- en omgeschreven cirkels

de Straal van de omgeschreven cirkel
eerst een hulpstelling:
    Als twee driehoeken een hoek gelijk hebben, dan verhouden hun oppervlakten zich
    als het product van hun zijden om die hoek.
Zie de figuur hieronder:

Notatie: laten we de oppervlakte van diehoek ABC schrijven als [ABC].

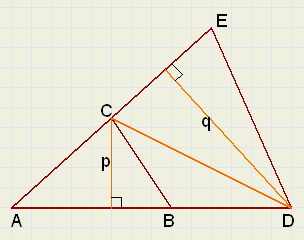DABC en DADE hebben LA gemeenschappelijk.
    [ABC] : [ADC] = (p.AB) : (p.AD) = AB : AD
    [ADC] : [ADE] = (q.AC) : (q.AE) = AC : AE
vermenigvuldigen met AC en met AD levert:
    AB : AD = (AB.AC) : (AD.AC)
    AC : AE = (AD.AC) : (AD.AE)
zodat
    [ABC] : [ADE] = (AB.AC) : (AD.AE)
Bekijk de figuur hieronder:

M is het middelpunt van de omgeschreven cirkel van ΔABC.

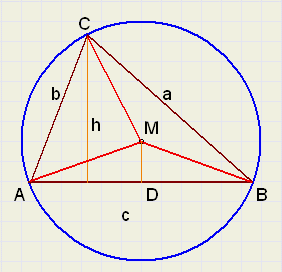Nu is, volgens de stelling van Thales:
    LDMB = 0,5*LAMB = LC
zodat:
    [ABC] : [DMB] = (AC.BC) : (DM.BM)
maar ook:



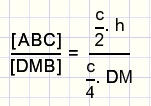
omdat
    BM = R {de straal}
    AC = b
    BC = a
    AB = c
volgt:



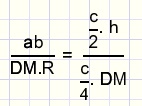
en



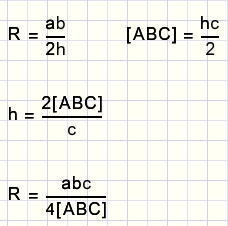
de straal van de Ingeschreven cirkel
Zie de figuur hieronder:
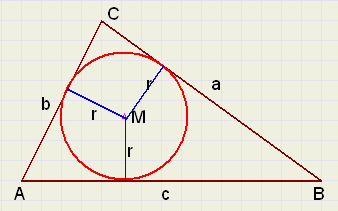    2 * [ABC] = ar + br + cr = r(a + b + c)
zodat:



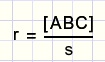
Opmerking: s is de halve omtrek van de driehoek.

de straal van de Aangeschreven cirkel
zie de figuur hieronder:
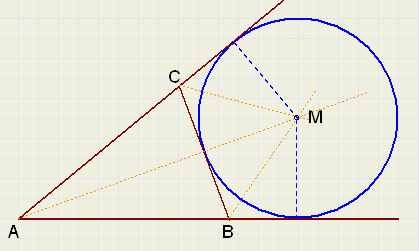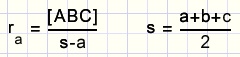
De straal ra van de cirkel met middelpunt M is



waarbij:
    BC = a
    AC = b
    AB = c
Het bewijs wordt aan de lezer overgelaten.

Voor wie zelf aan de slag wil:

r, ra , rb , rc zijn straal van de in- en aangeschreven cirkels van ΔABC.

bewijs dat: