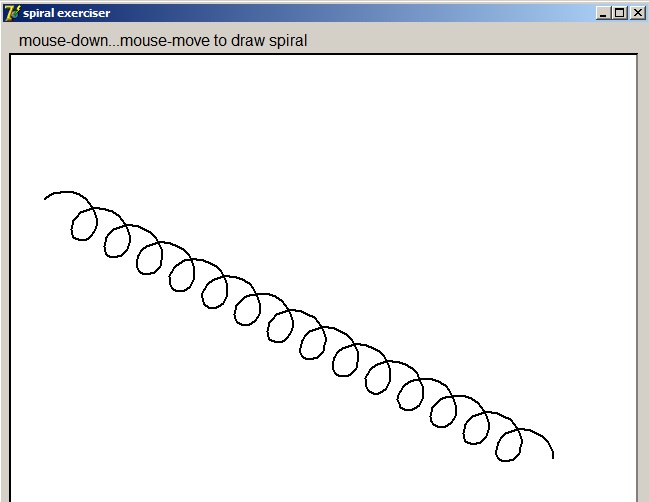
Spiralen tekenen

load program
load complete Delphi-7 project

In dit artikel leg ik uit hoe je spiralen tekent met de programmeertaal Delphi.
Bovendien wordt uw middelbare school kennis van de wiskunde opgefrist.



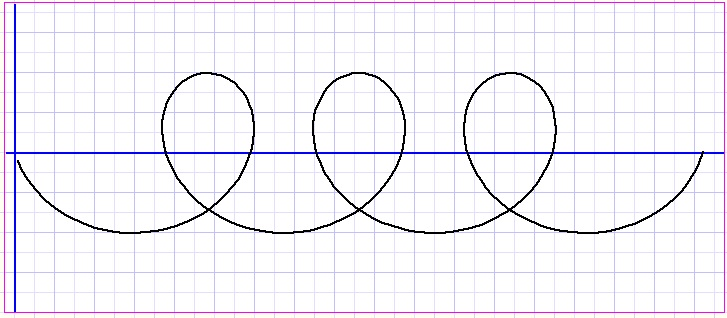
Tekenen van een spraal is de optelling van twee penbewegingen:
    1. tekenen van een cirkel (tegen de klok in) terwijl
    2. het middelpunt van de cirkel over een rechte lijn beweegt (van links naar rechts).

Hoeken meten in radialen

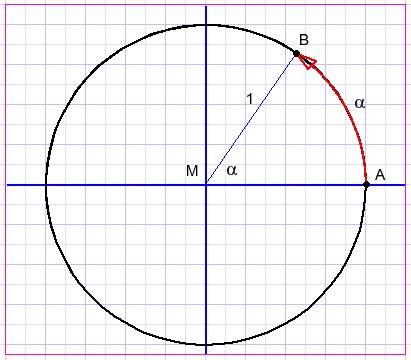
Beschouw een cirkel met straal 1.
We meten een middelpuntshoek a met de lengte van boog AB.
Omdat de omtrek van een cirkel met straal 1 gelijk is aan 2*pi,
is 2*pi radialen een hele omwenteling oftewel 360 graden.
Een middelpuntshoek van a radialen staat op een cirkelboog met lengte a
En bij een straal van r heeft de cirkelboog de lengte ar.



Cirkels tekenen

Een cirkel kan je tekenen door een punt P rond te laten lopen op afstand r van een middelpunt M.
Verbindt steeds de opvolgende punten P met rechte lijntjes.



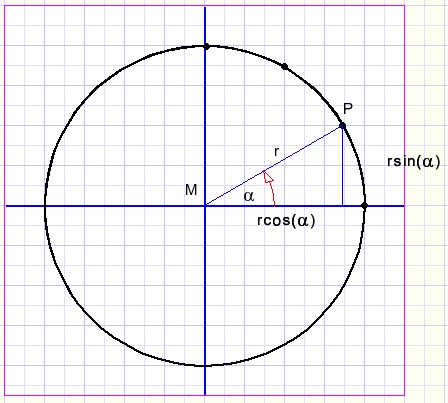
De hoek a wordt met kleine stapjes opgehoogd en steeds worden de coördinaten van P berekend:
    x = r.cos(a)
    y = r.sin(a)
De spiraal start op punt (x1,y1) en eindigt bij (x2,y2).
De afstand L tussen deze punten is : L = sqrt((x1-x2)2+(y1-y2)2).
De spiraal bovenaan deze pagina bekijkend zien we dat er een oneven aantal halve wendingen nodig zijn.
Afhankelijk van L 1, 3, 5, 7, ..... halve draaien.



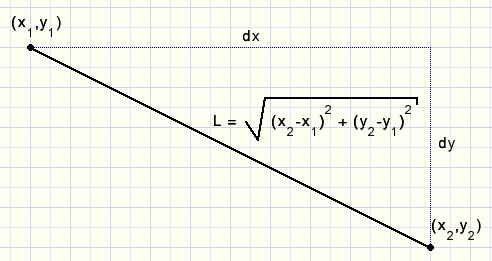
De volgende vraag is dus: "hoeveel halve draaien zijn er"?
We delen hiertoe L door straal r (maar een andere waarde dan r is ook goed).
Het quotient L/r moet daarna op het dichtsbijzijnde oneven getal worden afgerond.


Afronden op oneven gehele getallen (1,3,5....)

Geconfronteerd met een nieuw probleem grijpt de wiskundige terug op een vergelijkbaar maar simpeler probleem.
We weten hoe een getal op een gehele waarde wordt afgerond:
tel 0,5 bij, schrap cijfers achter de komma.(Delphi: truncate)
Een getal afronden op even waarde: tel 1 bij, deel door 2, truncate en vermenigvuldig met 2.
Nu de afronding naar een oneven waarde:
Trek 1 af, rond af op een even getal en tel 1 bij om het getal oneven te maken.
De bewerkingen -trek 1 af- en -tel 1 bij- neutraliseren elkaar.
Wat over blijft: deel het getal door 2, truncate, vermenigvuldig met 2, tel 1 bij.



Tekenen van de spiraal

Op het computer scherm neemt de y coördinaat neerwaarts toe.
Vergroten van een hoek levert rotatie met de klok mee.
In de volgende figuur begint de spiraal bij punt A(x1,y1) en eindigt bij B(x2,y2).
Het middelpunt van de cirkel beweegt van M1 naar M2.
M1-M2 = L - 2r.



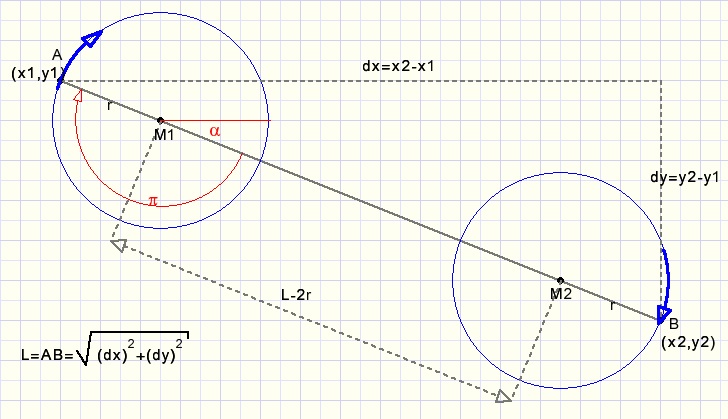
Als eerste stap berekenen we dx = x2-x1.
Daarna dy = y2 - y1.
Dan L = sqrt(sqr(dx) + sqr(dy)).
Dan: L/r en dit quotient ronden we af op het dichtsbijzijnde oneven getal, noem dit n.

De variable phi, hoek in radialen, controleert het tekenprocess.
phi loopt van 0 tot maxphi=n*pi, het aantal halve bogen.

In het plaatje hiervoor zien we echter dat phi moet starten op waarde a + p
deze afwijking noemen we phibias = arctan(dy/dx) + pi.
Als een halve cirkel in 12 stapjes wordt getekend dan moet phi steeds met een stapje pi/12 worden verhoogd.
dL is het bijbehorende stapje dat middelpunt M moet maken op de lijn AB.
dL = (L-2r)/maxphi.

Bij de start wordt de pen gezet op punt (x1,y1).
pL is de afstand AM: pL = r + phi*dL.
dxL = dx/L
dyL = dy/L
cirkel y coördinaat: a = r*sin(phi+phibias)
cirkel x coördinaat: b = r*cos(phi+phibias)
(sx,sy) zijn de coördinaten van M op lijn AB:
sy = y1 + dyL*pL
sx = x1 + dxL*pL
teken nu een lijntje naar (sx+b,sy+a)
volgende stap ...phi := phi + pi12

phi hoogt op tot waarde maxphi wordt overschreden.
In de berekeningen hierboven zijn de afrondingen op gehele getallen weggelaten.
Hiervoor verwijs ik naar de source code.

Een laatste punt is de relatieve positie van de punten A en B.
De enige variabele die moet worden aangepast is phibias,
als x1 > x2 dan moet de waarde pi niet worden bijgeteld.
Voor het geval x1 = x2 zijn een paar extra regels code nodig om delen door 0 te vermijden.

Het project

Het hele Delphi-7 project bestaat uit een form met een paintbox en een unit.
Mouse down, -move en -up events controleren een simpel teken mechanisme.
De straal r is gezet op 20.
Deze procedure tekent de spiraal: 
procedure paintcoil(x1,y1,x2,y2,r: smallint);
var phi,pi12,maxphi,phibias,dL,dx,dy,dxL,dyL : single;
    a,b,n,L,pL,sx,sy: smallInt;
begin
 pi12 := pi/12;
 dx := x2-x1;
 dy := y2-y1;
 if dx > 0 then phibias := pi + arctan(dy/dx)
  else if dx < 0 then phibias := arctan(dy/dx)
        else if y2 > y1 then phibias := -pi/2 else phibias := pi/2;
 L := round(sqrt(sqr(dx)+sqr(dy)));
 n := trunc(L/(2*r))*2+1;
 maxphi := n*pi;
 dL := (L-2*r)/maxphi;
 dxL := dx/L;
 dyL := dy/L;
 with form1.paintbox1.canvas do
  begin
   pen.width := 2;
   pen.color := $000000;
   moveto(x1,y1);
   phi := pi12;
   while phi <= maxphi do
    begin
     pL := r + round(phi*dL);
     a := round(r*sin(phi+phibias));
     b := round(r*cos(phi+phibias));
     sy := y1 + round(dyL*pL);
     sx := x1 + round(dxL*pL);
     lineto(sx+b,sy+a);
     phi := phi + pi12;
    end;
  end;//with
end;
Hieronder staat een plaatje met een resultaat: