

| het snijdende koorden probleem |  |
Het probleem hieronder werd op facebook gepubliceerd door Omid Motahed, docent wiskunde te Beijing.
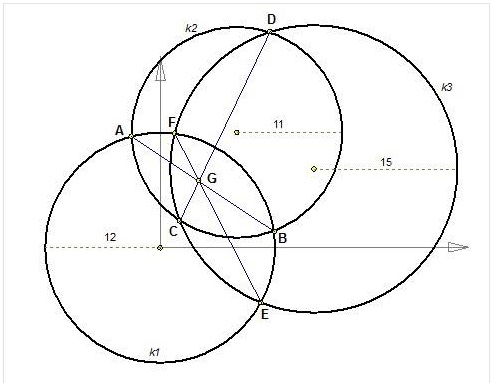
Drie cirkels snijden elkaar in twee punten.
De gemeenschappelijke koorden AB, CD, EF lijken door 1 punt (G) te gaan.
Gevraagd wordt deze eigenschap te bewijzen.
Dat is nog niet simpel.
Maar na een wat ongebruikelijke stap in ons denken wordt het duidelijk.
Voor dit bewijs grijpen we eerst even terug op een ogenschijnlijk heel ander probleem:
"hoe construeer je een willekeurige piramide"?
Eerst kiezen we een grondvlak, ABC:
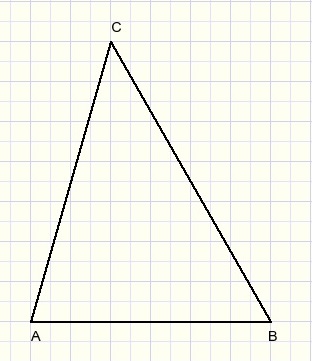
Dan kiezen we de projectie van de top (T) van de piramide op het grondvlak
en we tekenen meteen loodlijnen vanuit T op de zijden AB, BC, AC.
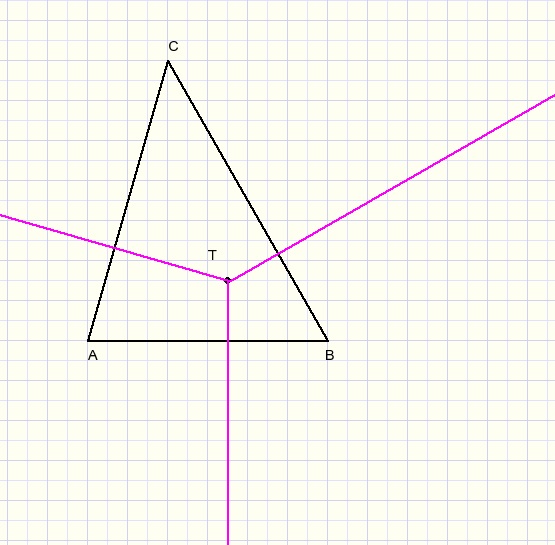
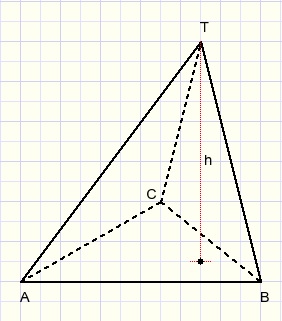
Nu de hoogte van de piramide kiezen, stel die is h (h loodrecht op TD), zie de figuur hieronder:
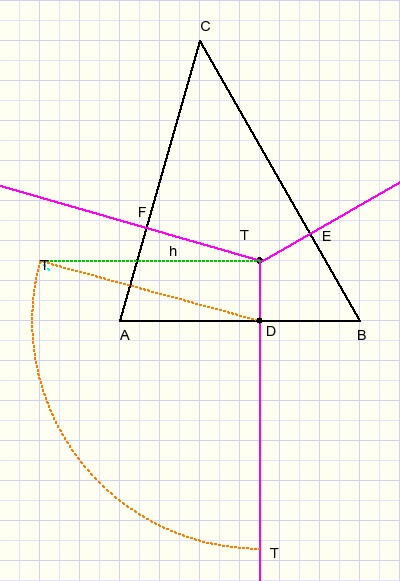
Punten T zijn allemaal hetzelfde, T ligt op hoogte h boven grondvlak ABC.
De gestippelde driehoek moet rond lijn TD worden gedraaid totdat h loodrecht op vlak ABC staat.
Neem nu D als middelpunt van een cirkel met straal TD.
Teken T1A, T1B.
Neem B als middelpunt en als straal T1B.
Neem C als middelpunt en als straal T2C.
Neem A als middelpunt en als straal T3A.
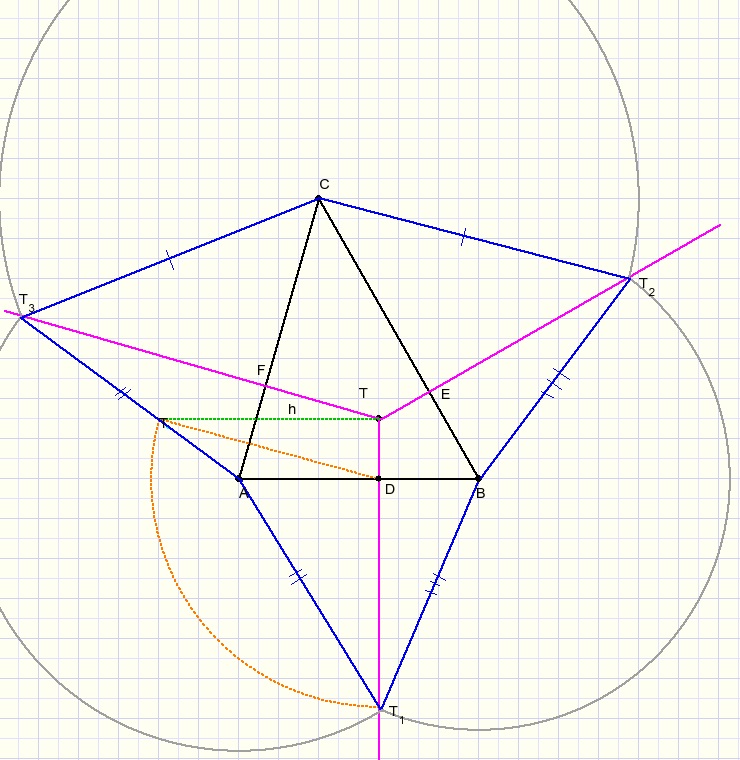
In bovenstaande figuur is dus:
-
BT1 = BT2
CT2 = CT3
AT1 = AT3
Draai nu vlak ABT1 om AB,
draai BCT2 om BC en
draai ACT3 om AC
totdat de punten T1 T2 T3 samenvallen.
Dat levert piramide TABC.
Nu terug naar het originele probleem:
We tekenen drie snijdende cikels met middelpunten A,B,C.
Beschouw nu ABC als het grondvlak van een piramide.
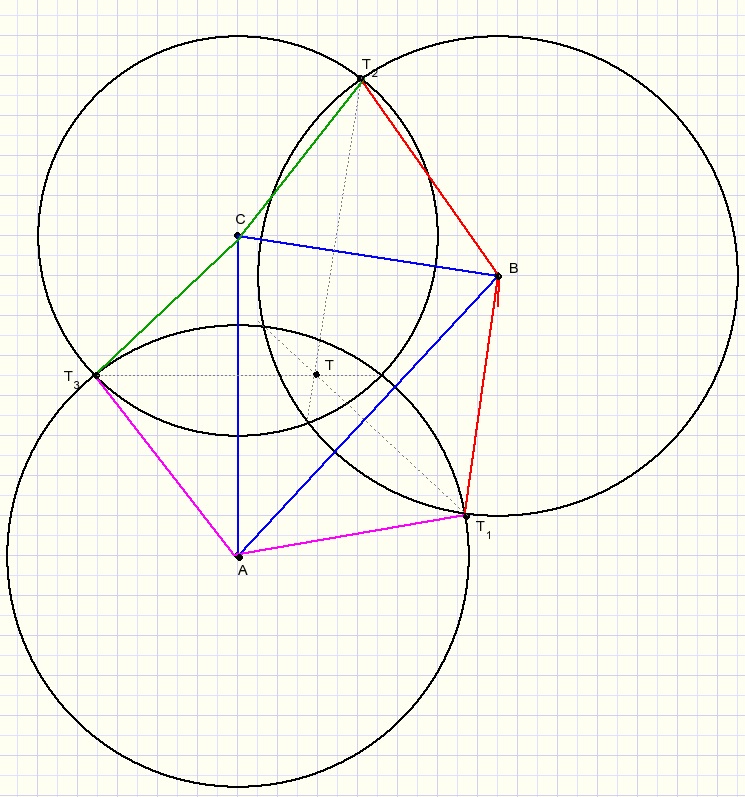
Merk op dat de rode-, groene- en paarse lijnstukken even lang zijn.
Vlakken ABT1, BCT2 en ACT3 zijn dan de zijvlakken van een piramide.
Draai nu deze vlakken om AB,BC en AC totdat de toppen T bij elkaar komen.
Punt G in de originele opgave is dan de projectie van de top T op het grondvlak.
De gemeenschappleijke koorden van de cirkels gaan dus door één punt.
Opmerking: als vlak ABT1 draait om lijnstuk AB, dan beweegt de projectie van T1
op vlak ABC over de gemeenschappelijke koorde van de cirkels A en B. Etc.
Hiermee besluit ik dit bewijs.

