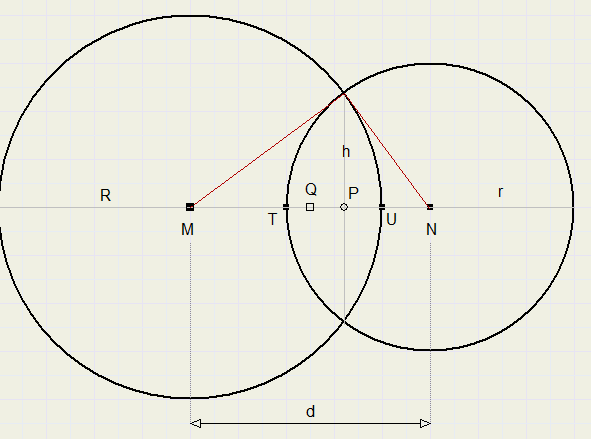
Snijdende Cirkels In dit artikel worden een paar formules afgeleid voor snijdende cirkels. Bekijk eens het plaatje hieronder. Twee cirkels van ongelijke grootte snijden elkaar. Gegeven zijn hun stralen (R en r) en de afstand d van hun middelpunten. Punt Q ligt op het midden van lijnstuk MN. MN = d Voor gegeven afstand d tussen de middelpunten en de stralen R en r berekenen we MT, TP, PU en UN. Pythagoras in de driehoek met basis MP en hoogte h: h2 = R2 - MP2 Pythagoras in de driehoek met basis NP en hoogte h: h2 = r2 - NP2 combinerend: R2 - MP2 = r2 - NP2 ....zodat MP2 - NP2 = R2 - r2 .................1) Op dit punt gekomen lijkt het of we zijn vastgelopen. Wat is het probleem? We zien één vergelijking met twee onbekenden (MP en NP) en die is niet oplosbaar. Maar nu gaan we een truc toepassen door inzet van punt Q, halverwege M en N. Daardoor kunnen MP en NP worden vervangen door één andere variabele, namelijk PQ en ziet de vergelijking is opeens wel oplosbaar. Het deel links van het = teken gaan we verbouwen. 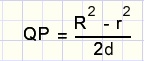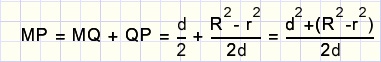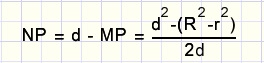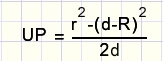MP2 - NP2 = (MP + NP)(MP - NP) Aangezien geldt MP + NP = d MQ = NQ MP = MQ + QP NP = NQ - QP....zodat MP - NP = MQ + QP - NQ + QP = 2QP kunnen we schrijven MP2 - NP2 = d(2QP) = 2d.QP waardoor, gecombineerd met ...1) We berekenen MP We berekenen NP Berekening van TP Uit UP = NP - NU volgt dan nog Aanbeveling: Bereken de lengte van het lijnstuk TU, een verrassende uitkomst.