De brekingswet van Snellius

Inleiding
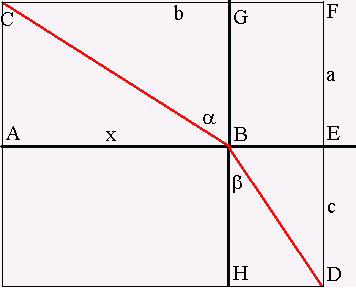In het plaatje hiernaast moet een wandelaar van punt C
naar punt D wandelen.
Boven de lijn AE is een heidelandschap, maar onder AE bevindt
zich een dicht bos, zodat de snelheid daar lager ligt.

We willen het pad vinden, waarover in zo kort mogelijke tijd
het traject wordt afgelegd.

De weg CAD is onverstandig: het langste deel van het traject
gaat dan door moeilijk begaanbaar gebied.
Ook de weg CED is waarschijnlijk niet de snelste, hoewel nu de weg
in het moeilijkste terrein zo kort mogelijk is.

Ergens tussen A en E, stel bij punt B, zal het beste punt liggen waar
van landschap wordt veranderd.

Om de positie van punt B te vinden spreken we af:
    de snelheid in het heideveld is v1
    de snelheid in het bos is v2
    EF = a
    CF = b
    DE = c
    AB = x
    hoek CBG = a
    hoek HBD = b
a,b,c,v zijn constanten. x moet worden berekend.

Formules voor de reistijd
We stellen de reistijd over het pad CB op t1 en over het pad BD op t2.

Volgens de stelling van Pythagoras is
    C B = 
    \a 2 + x 2
en
    B D = 
    \(b − x) 2 + c 2
zodat
    t1 = 
    \a 2 + x 2
    v1
en
    t2 = 
    \(b − x) 2 + c 2
    v2
De totale reistijd T = t1 + t2.

De vraag is: voor welke waarde van x heeft T een minimum?
Dat minimum vinden we door de afgeleide van T naar x op 0 te stellen.
Uit de aard van dit probleem volgt, dat dit nulpunt van de afgeleide geen maximum kan zijn.

Om schrijfwerk te besparen, differentiëren we t1 en t2 even afzonderlijk

Differentiëren van t1
 Stel a2 + x2 = p, dan is:
    d t1
    d x
     = 
    d t1
    d p
     · 
    d p
    d x
    d t1
    d x
     = 
    2 x p −0.5
    2 v1
    d t1
    d x
     = 
    x
    v1 B C
Differentiëren van t2
 Stel (b-x)2 + c2 = q en (b-x)2 = r dan is:
    d t2
    d x
     = 
    d t2
    d q
     · 
    d q
    d r
     · 
    d r
    d x
    d t2
    d x
     = 
    1
    v2
     · 
    −1 (2 (b − x)) q −0.5
    2
    d t2
    d x
     = −
    b − x
    v2 B D
zodat
    d T
    d x
     = 
    x
    v1 B C
     − 
    b − x
    v2 B D
    d T
    d x
     = 
    x (B D) v2 − (b − x) (B C) v1
    v1 v2 (B C) (B D)
    d t
    d x
     = 0

    x (B D) v2 = (b − x) (B C) v1
    B D
    b − x
     · 
    x
    B C
     = 
    v1
    v2
    sin a
    sin b
     = 
    v1
    v2
    dit is de wet van Snellius.
Van wandelaars naar lichtstralen
 Lichtstralen gaan volgens de snelste weg door een medium.
Als ze dat niet doen, dan worden ze ingehaald door de achterliggende golven en uitgewist.
In de figuur bovenaan deze pagina kan het wandelpad door de weg van een lichtstraal worden vervangen.

Het heideveld wordt lucht, het bos wordt bijvoorbeeld water.
De lijn AE is het grensvlak, waar de breking optreedt omdat licht zich in lucht sneller voortplant
dan in water.

In de optica heet
sin a
sin b
 de brekingsindex. De lijn HG heet de "normaal".

Deze wet werd in 1621 ontdekt door de Nederlandse wiskundige Willebrord Snell.