

| Repeterende breuken |  |
| Als we op de rekenmachine een breuk intikken zoals |
| dan zien we..... | = 0,333333.... |
Het cijfer 3 herhaalt eindeloos.
| Tikken we in ... |
| dan zien we..... | = 0,21212121.... |
Nu repeteert de cijfercombinatie 21... eindeloos.
Hoe zou dat komen?
En is het mogelijk om een breuk te verzinnen die bijvoorbeeld oplevert 0,112211221122.... of iets dergelijks?
Dat gaan we hier onderzoeken.
Eerst eens de staartdeling uitvoeren
3/1 \0,33333...
10
9
--
10
9
--
10
9
--
1
En ook de andere.
33/7 \0,21212121....
66
--
40
33
--
70
66
--
40
33
--
70
66
--
4
Na elke deling houden we een rest over.Herhaling van cijfers treedt op als we een rest krijgen, die al eerder voorkwam.
Bij de eerste deling is de rest steeds gelijk aan 1, hetzelfde cijfer in het antwoord repeteert.
Bij de tweede deling is de eerste rest 4, de tweede 7 en de derde opnieuw 4, zodat het patroon 21.. zich herhaalt.
We gaan een breuk fabriceren, die oplevert 0,191919.... er herhalen steeds 2 cijfers.
Laten we die breuk B noemen, dus B = 0,191919.... dan is
-
100B = 19,191919... oftewel
100B = 19 + B.......zodat
99B = 19......en
Een breuk bij 0,124812481248... is dus
-
10000B = 1248 + B
9999B = 1248
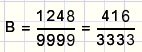 |
Heb je de truuk door?
Als we een willekeurige breuk als tiendelige breuk schrijven, dan zal altijd herhaling van cijfers optreden.
Bijvoorbeeld bij deling door 7 zijn resten 0..6 mogelijk, dus of de deling komt precies uit met antwoord ...,000000
of er treedt herhaling op na maximaal 6 cijfers, dus hooguit 6 cijfers herhalen steeds.
Nu kunnen we natuurlijk ook cijferreeksen opschrijven die niet herhalen.
Daar hoort dan geen breuk bij.
Een voorbeeld daarvan is de wortel uit 2 = 1,414213562..... nooit herhaling van cijfers.
| We hadden ook een ingewikkelder manier kunnen gebruiken, want in het geval van |
-
0,33.... = 0,3 + 0,03 + 0,003... = 3(0,1 + 0,01 + 0,001...)
| De som daarvan is |  |
Vermenigvuldigd met 3 levert dat weer de breuk één derde op.

