recursief GGD berekenen

download GCD program
download Delphi-7 GCD project

Dit artikel beschrijft een recursieve methode om de GGD (Grootste Gemeenschappelijke Deler)
van twee getallen te berekenen.
Uitgangspunt is het theorema van Euclides, wat simpelweg neerkomt op:
    GGD(a,b) = GGD(a-b,b)
Voorbeeld:
GGD(60,45) = GGD(15,45) = GGD(45,15) = GGD(15,15) = GGD(0,15) = 15.

Korter:
60 mod 45 = 15, GGD(60,45) = GGD(15,45) = GGD(45,15)
45 mod 15 = 0, GGD(45,15) = GGD(0,15) = 15.

Recursieve procedures en functies kunnen zichzelf aanroepen.
Dat levert heel compacte code op die echter vaak moeilijk is te doorgronden.
Duidelijkheid ontstaat door deze procedure in veelvoud in gedachten te nemen, zie het plaatje hieronder:



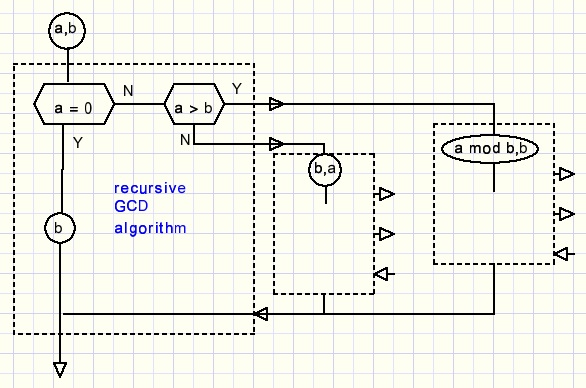
Dit is de functie: (GCD is Engels voor GGD) 
function GCD(a,b : Int64) : Int64;
//b <> 0
begin
 if a = 0 then result := b
  else if a < b then result := GCD(b,a)
   else result := GCD(a mod b,b);
end;
Dat is alles !
Met het programma zijn de GGD van getallen tot 12 cijfers te berekenen.
Voor details verwijs ik naar de source code.