Recursief logaritmes berekenen

download programma
download Delphi-7 project

In dit artikel beschrijf ik hoe met een recursief programma de logaritme uit een getal kan worden berekend.
De programmeertaal is Delphi.

Kettingbreuken

De algemene vorm van een kettingbreuk is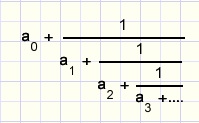



waarbij ai een geheel getal is > 0.
De invloed van ai wordt bij toenemende i steeds geringer.
Met kettingbreuken is steeds het gehele deel van een getal af te splitsen
waarna een deel overblijft dat kleiner is dan 1.
De reciproke daarvan is weer groter is dan 1 zodat weer het gehele deel is af te splitsen.
Zo'n zichzelf herhalend proces is prima te vatten in een recursieve procedure.
Hier passen we dit principe toe om de logaritme van een getal te berekenen.

Logaritmes

glog(a) = x betekent: gx = a
De logaritme uit een getal nemen komt dus neer op het schrijven van dat getal als een
grondtal tot een macht en vervolgens dat grondtal te verwijderen zodat de macht overblijft.

Enkele rekenregels voor logaritmes zijn:
    glog(g) = 1
    glog(an) = n.glog(a)
    glog(a.b) = glog(a) + glog(b)
    alog(b) = glog(b)/glog(a)...waar uit volgt
    alog(b) = 1 / blog(a)
We gaan blog(a) berekenen en veronderstellen dat a > b.
(b : base).
a herschrijven we : a = bc.x
c is een positief geheel getal zodanig dat bc < a < bc+1.
De overblijvende factor x = a/bc < b.
    blog(a) = blog(bc.x)
    =blog(bc) + blog(x)
    =c + blog(x)
    =c + 1 / xlog(b)
waarna het proces zich herhaalt omdat b > x.

Recursie

Recursieve procedures roepen zichzelf aan.
Omdat de parameters en de lokaal gedeclareerde variabelen op het stack staan,
zijn die variabelen voor elke aanroep unniek.
Recursieve procedures zijn enorm krachtig maar vaak moeilijk te begrijpen.
Wat dan helpt is om in gedachten er van uit te gaan dat het verschillende procedures zijn,
die hetzelfde doen.

Het programma

Hier is de recursieve functie: 
function recLog(b,a : double) : double;
//recursive logarithm calculation
//b : base; a : number
var c : byte;
    b2,bt : double;
    GO : boolean;
begin
 c := 0;
 b2 := 1;
 repeat
  bt := b2 * b;
  GO := a >= bt;
  if GO then begin
              inc(c);
              b2 := b2 * b;
             end;
 until GO = false;
 a := a/b2;
 if a > 1.000001 then result := c + 1/reclog(a,b)
  else result := c;
end;
Bij elke stap nadert a dichter tot 1 en dat is ook de test om
de functie opnieuw aan te roepen voor een extra stap.

Variable c is de grootste macht van b die nog in a past.
De achtereenvolgende waarden van c vormen dus de kettingbreuk.

Voor verdere details van dit Delphi-7 project verwijs ik naar de source code.