Hoeken meten in Radialen

Inleiding
Een wetenschappelijke rekenmachine kan naast graden, ook worden ingesteld
om te werken met hoeken in radialen.
In dit artikel wordt uitgelegd wat radialen en de voordelen daarvan zijn.
Als toepassing wordt oa. de formule van een cycloïde berekend.

Opmerking:
Engels voor graden is "degrees".
Engels voor radialen is "radians".

Wat zijn radialen?


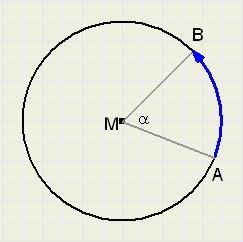
Bekijk het plaatje hierboven.
Afgebeeld is een cirkel met middelpuntshoek a
en bijbehorende cirkelboog AB.

Als a wordt gemeten in graden, dan is de
lengte van boog AB =
als R de straal is van de cirkel.

Bij afspraak is een volle hoek (3600 ) gelijk aan 2p radialen,
zodat bij meting in radialen de booglengte AB gelijk is aan
    De booglengte in radialen wordt eenvoudig verkregen door de middelpuntshoek
    te vermenigvuldigen met de straal.

We kunnen ook schrijven:
Een (middelpunts) hoek (in radialen) is de verhouding van booglengte en straal.

Dat maakt de radiaal tot een factor, een dimensieloos getal,
wat zeer handig is in formules.

Omrekenen van graden naar radialen
Tussen radialen en graden bestaat een recht-evenredig verband,
zodat omrekening inhoudt : vermenigvuldigen met een constante waarde.

Als we door vermenigvuldiging een getal A willen veranderen in B,
dan moet worden vermenigvuldigd met
immers

Omdat 360 graden overeenkomt met 2p radialen is de omrekeningsfactor
van graden naar radialen dus:
Eén graad is dus 0,017453.... radialen.

Voorbeeld

Omrekenen van radialen naar graden
Nu is de omrekeningsfactor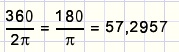
Eén radiaal is dus 57,2957.... graden.

Voorbeeld
0,523598775 rad. = 0,523598775 * = 30 graden.

de sinus van kleine hoeken
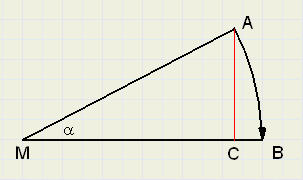
Bekijk eens het plaatje hieronder:


Er geldt:


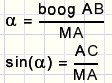Voor kleine hoeken zal het verschil boogAB - AC steeds dichter tot 0 naderen, zodat geldt:
    sin(a) » a
Sterker nog:


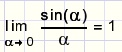wat formules sterk vereenvoudigt, zoals straks zal blijken.

Ter illustratie een tabelletje, dat de fout aangeeft bij vervanging van de sinus door de hoek :
    gradenradialensinusrelatieve fout
    200,349065850,34200201432,02%
    100,1745329250,1736481770,51%
    50,00872664620,0871557420,13%
    10,0174532920,0174524060,005%

de afgeleide functie van de sinus

De algemene formule voor de afgeleide (richtingscoëfficiënt) van een functie f(x) luidt:


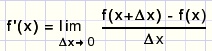Toegepast op f(x) = sin(x), waarbij x in radialen:


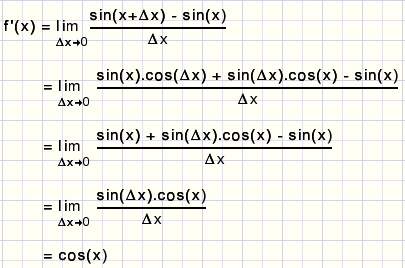Opmerkingen

We maakten gebruik van


de Cycloïde
Een toepassing van het gebruik van radialen.
Bekijk eens het plaatje hieronder:


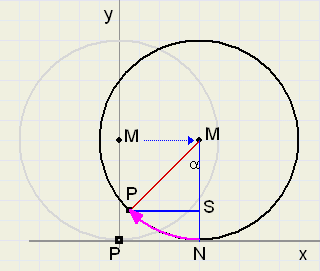
Een cirkel rolt over de x-as.
We zoeken een formule voor de beweging van het punt P op deze cirkel.

In de uitgangspositie ligt P op de oorsprong.
Wanneer de cirkel een stukje naar rechts is gerold volgt uit het plaatje:
    1. booglengte PN = verplaatsing over x-as
    2. boog PN = a *MP
We nemen als straal r, dus r = MP.
De formule bepalen in zg. parametervorm:
x en y drukken we uit in draaihoek a .

Voor het gedraaide punt P geldt dan:
    xp = a r - r*sin(a)
    yp = r - r*cos(a)
Met het grafiekenprogramma Graphics-Explorer tekenen we de baan van P.
Omdat Graphics-Exporer werkt met variabele v in parameterfuncties
en constanten a,b en c moet worden ingevoerd:
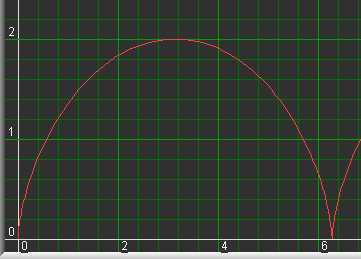
    x = v*a - a*sin(v) ; y = a - a*cos(v)
De amplitude is zodoende te wijzigen door verandering van a.
Selecteer hiervoor "vervangen" en "autoplot" mode.

Voor het plotten wordt gevraagd om het domein van v en het aantal stappen.
Vul in
    begin : 0
    einde : 30
    stappen : 500
Hieronder staat het resultaat.

Voor weergave in graden moet v die niet binnen sin() of cos() staat
in de formule worden vervangen door
    v / ( 180 / p ) = 0,017453v
en de x-as moet met een factor 180 / p worden opgerekt.
Ook moet in Graphics-Explorer de mode
"graden" geselecteerd worden.

Voer de formule in:
    x = (0,01745v*a - a*sin(v))*57,2958 ; y = a - a*cos(v)
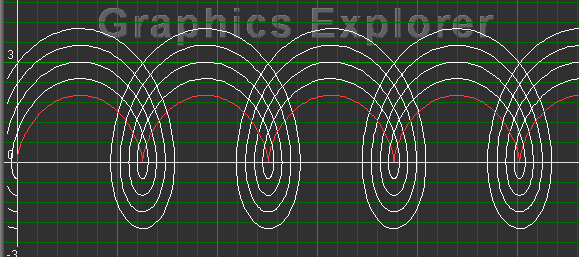
Neem voor het domein van v : 0 ....1000 in 1000 stappen.

Interessant is ook het geval waar P zich binnen of buiten de cirkel (aan een staafje) bevindt.
Als PM = R, ga dan na hoe de formule verandert.

Plot het resultaat door b te nemen voor R.
Met een paar muiskliks is nu het effect te zien bij verschillende waarden van R en r (a en b).

Hieronder tot slot het resultaat (even mode "toevoegen" geselecteerd voor het effect):