Pythagoras drietallen

Drie gehele getallen (a,b,c) heet een "Pythagoras drietal" als geldt: a2 + b2 = c2

Merk op: bij berekeningen met de stelling van Pythagoras komen in het antwoord meestal wortels voor.
Het bekendste Pythagoras drietal is (3,4,5) want 32 + 42 = 52

Zouden er nog meer drietallen zijn?

Op zoek
    a2 + b2 = c2
    b2 = c2 - a2
    b2 = (c - a)(c + a)
stel nu:
    c - a = x2
    c + a = y2.............zodat

    b2 = x2y2
    b = xy
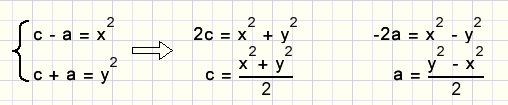
nu lossen we het volgende stelseltje vergelijkingen op



De oorspronkelijke formule a2 + b2 = c2 kan nu herschreven worden als:



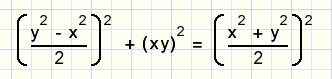
Samenvattend:
    a = y 2 − x 2
    b = 2 x y
    c = y 2 + x 2
Voor elk paar gehele getallen (x,y) kan nu a,b en c worden berekend.

Conclusie

Er zijn oneindig veel pythagoras drietallen.

Sommige drietallen zijn flauw, ze zijn gewoon en veelvoud van een ander drietal.
Originele drietallen zullen geen gemeenschappelijke factoren bezitten oftewel er geldt : ggd(a,b) = 1


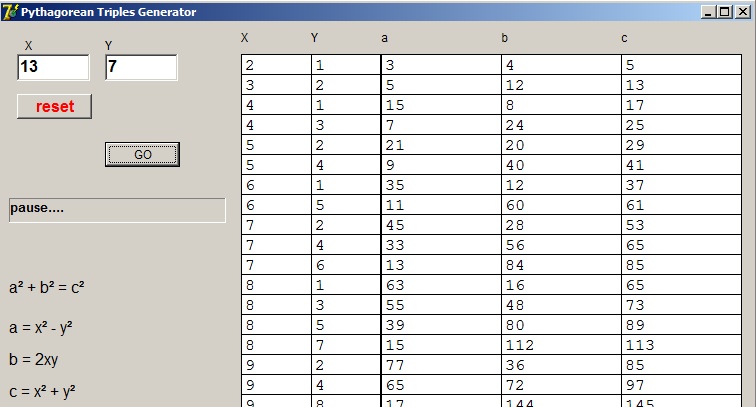
Resultaten

Een klein Delphi programma berekent de Pyhagoras drietallen:



download program (zip format)
download complete Delphi-7 project