de Stelling van Pythagoras

Inleiding
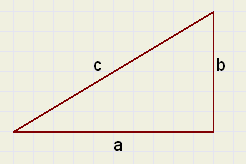In een rechthoekige driehoek met rechthoekszijden a en b en schuine
zijde c geldt de formule:

    a2 + b2 = c2

Deze formule staat bekend als de stelling van Pythagoras.
Zie figuur hiernaast.

Deze stelling is het uitgangspunt van veel andere stellingen en berekeningen.
In dit artikel worden vijf bewijzen geleverd.

Bewijs -1-
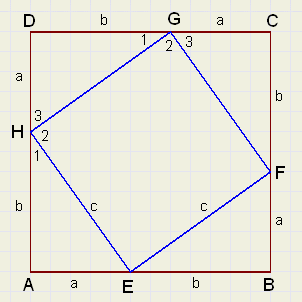We gaan uit van het vierkant ABCD.
Op de zijden hiervan zijn de punten E,F,G en H
zo geplaatst, dat AE = BF = CG = DH.
Deze afstand noemen we a.
Elke zijde van het vierkant ABCD heeft verder
de lengte a + b.

Het bewijs bestaat uit 2 delen. Eerst moet worden
vastgesteld, dat EFGH een vierkant is.
Uit de constructie volgt, dat driehoeken
AEH,BFE,CGF en DHG gelijk zijn. EFGH is dus in
ieder geval een ruit en de lengte van een zijde noemen we c.
De hoeken (1) en (3) zijn samen 90 graden, zodat voor hoek (2)
90 graden overblijft.
EFGH is daarom een vierkant.

Het tweede deel van het bewijs:
We beschouwen de oppervlakten en zien:

    opp. ABCD = 4 * opp.AEH + opp.EFGH
    (a + b)2 = 2ab + c2
    a2 + 2ab + b2 = 2ab + c2
    a2 + b2 = c2

Bewijs -2-
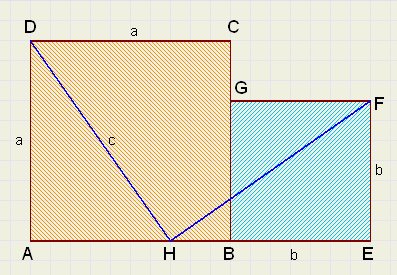Nu is het uitgangspunt twee tegen elkaar
geplaatste vierkanten: ABCD (met zijden a)
en BEFG met zijden b.
Op AB wordt punt H zo geplaatst, dat AH = b.
Daaruit volgt, dat HE = a.

We pakken de schaar, knippen de
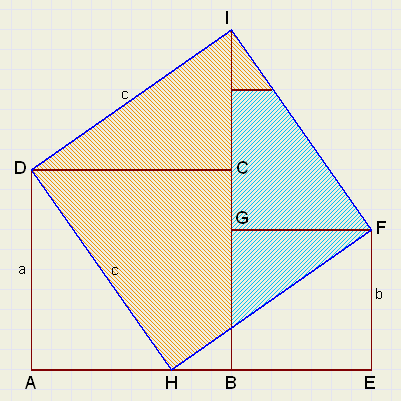driehoeken ADH en HEF af en plaatsen
die op de zijden DC en GF.

Op eendere wijze als bij bewijs -1- kan
worden beredeneerd, dat HFID een vierkant is.

Uit de kleuring volgt:
    a2 + b2 = c2


Bewijs -3-
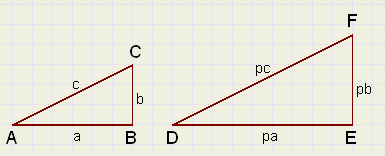Eerst een aanloopje.
Hiernaast zie je de driehoeken ABC en DEF.
Deze driehoeken zijn gelijkvormig:
de ene is een vergroting van de andere en
wel met een factor p.

Let hierbij goed op de overeenkomstige zijden:
AB en DE, of AC en DF.
Gelijkvormige driehoeken hebben de eigenschappen dat
    - overeenkomstige hoeken gelijk zijn
    - verhoudingen tussen hun zijden gelijk zijn
Omgekeerd geldt, dat wanneer twee driehoeken gelijke hoeken bezitten,
ze gelijkvormig zijn.
Deze eigenschappen zijn te bewijzen door grote rechthoeken te stapelen uit
(gelijkvormige) kleine rechthoekjes. Elk rechthoekje is te splitsen in twee
rechthoekige driehoekjes, enzovoorts.

Hulpstelling

    De oppervlakten van twee gelijkvormige driehoeken verhouden zich
    als de kwadraten van twee overeenkomstige zijden.
Het bewijs verloopt als volgt: (zie figuur hierboven)
De dubbele oppervlakte van de driehoeken is ab en abp2.
Hun oppervlakten verhouden zich dus als 1 : p2 en dat is ook
de verhouding tussen de kwadraten van twee overeenkomstige zijden.

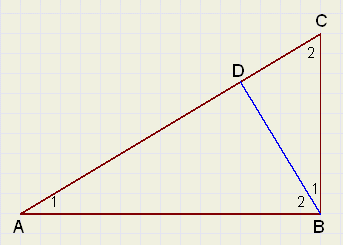In de figuur hiernaast staat BD loodrecht op AC en
AB staat loodrecht op BC.
In deze figuur zitten drie gelijkvormige driehoeken:
ABC, ADB en BDC.
Let op: de volgorde van de hoekpunten is belangrijk,
het geeft de overeenkomstige zijden aan.
De gelijke hoeken zijn met eenzelfde cijfer aangegeven.

Met deze voorkennis verloopt het bewijs als volgt:

(Noem AB = a , BC = b en AC = c en beschouw de overeenkomstige schuine zijden
van de driehoeken)

Er geldt:
    opp.ADB + opp.BDC = opp.ABC
    opp.ADB : opp.ABC + opp.ABC : opp.ABC = 1

en wegens de verhouding van de oppervlakten (hulpstelling):
    a2 : c2 + b2 : c2 = 1
    a2 + b2 = c2
Bewijs -4-
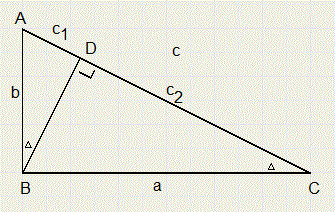Dit bewijs gaat uit van gelijkvormigheid.

1.
    DABD ~DBCD
    c1 : b = b : c
    c1c = b2
2.
    DBCD ~DACB
    c2 : a = a : c
    c2c = a2
1. en 2. optellen
    a2 + b2 = c2c + c1c = (c2 + c1)c = c2

Bewijs -5-
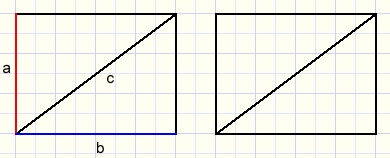Neem twee gelijke rechthoeken met zijden a en b.
Knip die doormidden over de diagonaal,
dat levert vier gelijke rechthoekige driehoeken op.
De schuine zijde heeft lengte c.

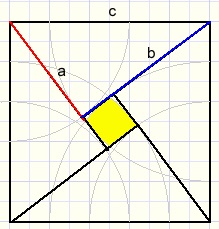Leg de driehoeken neer zoals in het plaatje rechts.

Het hele vierkant heeft oppervlakte c2.
De originele rechthoeken hebben oppervlakte 2ab.
Het ingesloten gele vierkantje heeft oppervlakte (b-a)2.
Zodat:
2ab + (b-a)2 = c2
2ab + b2 - 2ab + a2 = c2
a2 + b2 = c2