de beste Puntzak

Inleiding
In dit artikel worden de optimale afmetingen van een puntzak bepaald.
We onderzoeken daarvoor de verhouding tussen inhoud en oppervlakte.
Deze verhouding moet, om verspilling van papier te vermijden, zo groot mogelijk zijn.

De bedoeling is ook om het resultaat met minimale inspanning te verkrijgen:
de goede wiskundige is immers van nature lui.

De Constructie
Een puntzak wordt verkregen door een segment uit een cirkelvormig stuk papier te knippen
en vervolgens de delen tegen elkaar te plakken zodat het middelpunt de top wordt van een kegel.
In dit artikel vergeten we de plaknaden.
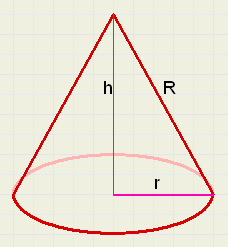
Zie de figuur hieronder, de punt-zak is een punt-muts geworden, dat tekent wat prettiger.
Geen overbodig werk
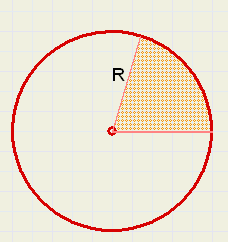De hele cirkel heeft een oppervlakte pR2.
Stel, dat we een segment uitknipten met een hoek van a graden.
Het uitgeknipte segment heeft een oppervlakte van pR2.(a/360)

Het gebruikte papieroppervlak is dus
    pR2 - pR2.(a/360)
In de figuur zien we dat het oorspronkelijke stuk papier met straal R nu een kegel is geworden.
Het grondvlak heeft een kleinere straal r en de hoogte is h.

De oorspronkelijke cirkel heeft een omtrek van 2pR.
De booglengte van het uitgeknipte segment is : 2pR.(a/360)
De overgebleven boog is de omtrek van de kleine cirkel met straal r, zodat geldt:
    2pr = 2pR - 2pR.(a/360)
Na vereenvoudiging:
    r = R - R.(a/360)
de verhouding inhoud : oppervlakte noemen we Y.
Voor deze verhouding doet R er niet toe.
Dus kiezen we gemakshalve R = 1.
Het gebruikte papieroppervlak is nu:
    p2 - p2.(a/360)
De inhoud van een kegel is gelijk aan: één derde van oppervlakte grondvlak x hoogte, dus
    pr2h/3
De verhouding Y = inhoud : papieroppervlak wordt
    Y = (pr2h/3) : (pR2 - pR2.(a/360))
Na vereenvoudiging
    Y = (r2h/3) : (1 - a/360)
Maar (1 - a/360) = r zodat
    Y = rh/3
waarbij geldt (zie figuur)
    r2 + h2 = 1
zodat
    Y = 
    r 
    \1 − r 2
    3
Om het maximum te vinden moet Y naar r worden gedifferentieerd,
waarbij de product- en de ketttingregel worden toegepast:
    Y' = 
    1
    3
    		 
    æ
    \1 − r 2
    		 + 
    r (−2 r)
    2 
    \1 − r 2
    		ö
    ­­
    èø
Na vereenvoudiging:
     
    Y'    		 
     = 
    1
    3
     (1 − 2 r 2)
    \1 − r 2
Voor het maximum van Y moet zijn
    1 - 2r2 = 0
zodat
    r = 0,707106 ..............{uitgaande van R = 1}
en omdat r = 1 - a/360:
    a = 105,44 graden

Maar de eenvoudigste conclusie is natuurlijk:
    bij de optimale puntzak zijn de hoogte en straal van het grondvlak gelijk

Een grafische oplossing kan worden gevonden met Graphics-Explorer
Vervang r door x en plot de formule
    y = (x * sqrt(1 - x^2)) / 3
Het maximum kan scherper worden afgelezen, door ook y = d:(x * sqrt(1 - x^2)) / 3.....
oftewel de afgeleide te plotten.
Gebruik daarvoor dan een andere kleur en zoom in op het snijpunt met de x-as.
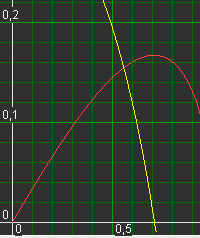De rode grafiek in het plaatje hierboven geeft het verband tussen de verhouding
inhoud:oppervlakte (Y) en de straal van het grondvlak (X).
De gele lijn is de afgeleide functie.