de Pizza stelling E.C.Buissant des Amorie
D.E.Dirkse

Wat is de "PIZZA" - stelling?
Bekijk eens figuur 1 hieronder.
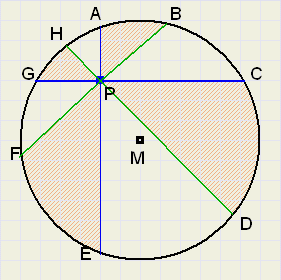    fig.1

M is het middelpunt van een -cirkelvormige- pizza.
P is een willekeurig punt binnen de cirkel.
A,B,C,...,H zijn punten op de cirkel.
AE is een willekeurige lijn door P.
Verder geldt:
AE ^ GC , BF ^ DH, LAPB = 45o
De cirkel heeft een straal r.

De "PIZZA" stelling luidt:
    de oppervlakten van de wel- en niet-gearceerde delen zijn gelijk.
In dit artikel wordt deze stelling bewezen.
Het bewijs bestaat uit de volgende stappen:
    1. een hulpstelling : AP2 + CP2 + EP2 + GP2 = 4r2
    2. we tonen aan, dat de grootte van de gearceerde oppervlakte niet verandert als A,B,C,..,H verschuiven
Vergelijk fig.1 en fig.2 :
Een gevolg van de stelling is, dat de gearceerde oppervlakten in beide figuren gelijk zijn.

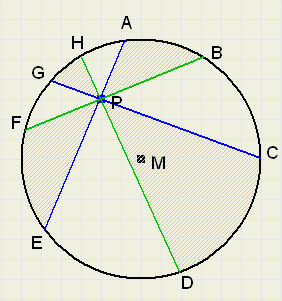    fig.2
Bij 45o verdraaiing zijn de wel- en niet-gearceerde delen dan van plaats verwisseld.
Zodat hun oppervlakten even groot zijn.

De hulpstelling
Zie figuur 3:
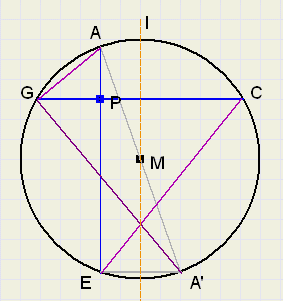    fig.3
Toepassing van de stelling van Pythagoras:
    AG2 = AP2 + GP2
    CE2 = CP2 + EP2
We spiegelen A in punt M, dat levert punt A'.
Wegens lijnsymmetrie:
    A'G = CE
LAGA' staat op de halve cirkelboog, zodat (stelling van Thales)
    LAGA' = 90o en (Pythagoras):
    (AA')2 = AG2 + A'G2
Alles combinerend:
    (AA')2 = AP2 + GP2 + A'G2
    (AA')2 = AP2 + GP2 + CE2
    (AA')2 = AP2 + GP2 + CP2 + EP2
Oftewel:
    AP2 + GP2 + CP2 + EP2 = (2r)2

Het bewijs
Zie figuur 4:
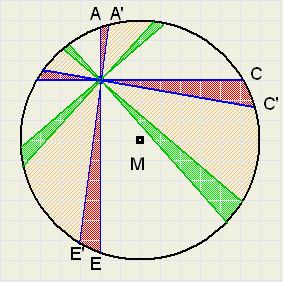    fig.4
Alle lijnen draaien met een kleine hoek Dj
Daardoor verschuift punt A naar A', B naar B', C naar C', enzovoorts.

Het gearceerde cirkelsegment bij A zal hierdoor iets in grootte veranderen.
Er gaat iets af: dat is met de kleur rood aangegeven.
Er komt ook iets bij: dat is met de kleur groen aangegeven.

Eenzelfde verhaal geldt voor de andere gearceerde cirkelsegmenten.
De gearceerde oppervlakte O is een functie van de draaihoek j
    O = f(j)
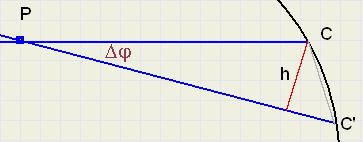We beschouwen een vergroting van zo'n verandering van een segment: (fig.5)
    fig.5
In fig.5 is de hoogte h van DPC'C
    h = PC.sin(j)
zodat:
    O = 0,5.PC'.PC.sin(j)

We differentiëren O naar de draaihoek j
    O' = 
    lim
    0.5 (P C) (P C') ·  sin (D j)
    D j
    D j → 0

zodat:
    O' = 0,5.PC2

Immers:
    lim
    sin (D j)
    D j
    D j → 0
     = 1
    en PC' nadert tot PC
Als O de som is van alle gearceerde delen dan is:
    O' = -0,5PA2 + 0,5PB2 - 0,5PC2 + 0,5PD2 - 0,5PE2 + 0,5PF2 - 0,5PG2 + 0,5PHA2
    O' = 0,5(PB2 + PD2 + PF2 + PH2 - (PA2 + PC2 + PE2 + PG2))
maar volgens de hulpstelling is:
    PA2 + PC2 + PE2 + PG2 = (2r)2

    en dus ook:

    PB2 + PD2 + PF2 + PH2 = (2r)2
zodat : O' = 0

Maar dan moet gelden: O = constant

De grootte van het gearceerde deel is dus constant, onafhankelijk van de draaiing.

Bij draaiing over 45o zijn de wel- en niet-gearceerde delen verwisseld.
Deze delen zijn dus altijd gelijk.

Hiermee heb je een ludieke manier in handen om een pizza eerlijk in tweeën te delen.

Eet smakelijk!