Een pendule simulator

download pendule simulator programma

Deze pendule, of slingertijd meter, is een klein Delphi project.

Hieronder staat een verkleind plaatje:



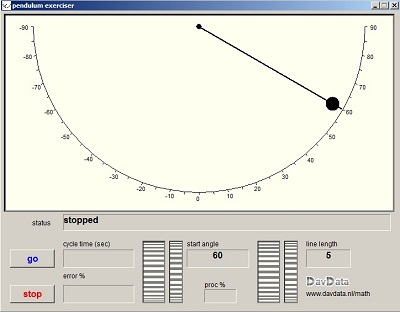
Draaiknopjes stellen de hoek in waaruit het gewicht wordt losgelaten en de lengte van de kabel.

Werkwijze

    - stel de hoek in (houd muisknop ingedrukt, beweeg muispointer over de knopjes)
    - stel de kabellengte in (..)
    - druk go knop in om het gewicht los te laten

Druk op stop om de beweging te stoppen.

Vensters tonen:
    - de slingertijd
    - de nauwkeurigheid
    - percentage van de tijd die de processor nodig heeft voor de simulatie en het tonen van de slinger.
Download dit (Windows) programma met een muisklik op het bliksem icoontje hierboven.

Opmerking: Het programma telt luchtweerstand niet mee.

Basiskennis kinematica

De eenheid van lengte is de meter (m).
De eenheid van tijd is de seconde (sec).

In geval van een constante beweging:
afstand = snelheid * tijd.
s = vt {s : afstand (m), v : snelheid (m/sec), t : tijd (sec)}

Versnelling is snelheidsverandering per seconde.
In geval van constante versnelling:
v = at {v: snelheid (m/sec), a: versnelling (m/sec^2), t: tijd (sec)}



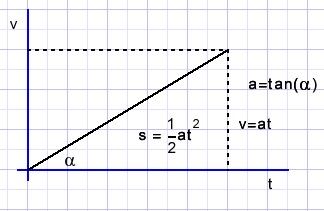
Afstand is de oppervlakte van de driehoek:
    s = 0.5at2
Bij constante versnelling:
Als vt de snelheid is van een voorwerp op tijdstip t dan:
    vt = v0 + at
Als st de afgelegde afstand is in t seconde:
    st = v0t + 0.5at2
De eenheid van massa is de kilogram, ongeacht de zwaartekracht.
De eenheid van kracht is de Newton (N).
Eén Newton (N) is de kracht die een massa van 1 kg. een versnelling geeft van 1 meter per sec/sec.
De snelheid van die massa neemt dan elke seconde met 1 m/sec. toe.

F = ma {F: kracht (N), m: massa (kg), a: versnelling (m/sec2)}
Op aarde geeft de zwaartekracht aan een vallend voorwerp een versnelling van 9,8m/sec^2, die noemt men g.

Mechanische energie het het product van kracht en afstand.
De eenheid van energie is de Joule (J).
E = Fs {E: energie (J), F kracht (N) s: afstand (m).

Om een massa van m kg. over h meters op te tillen tegen de zwaartekracht in kost aan energie
    Ep = mgh {Ep: potentiële energie (J)}
Energie gaat nooit verloren maar kan omgezet worden in een andere vorm zoals chemische energie in een batterij.
Of in warmte.
Een massa m wordt gedurende t seconden versneld met a (m/sec2).
De afgelegde afstand is dan s = 0.5at2.
Energie E = Fs = F*0.5*at2
Omdat F=ma:
E = 0.5ma2t2
omdat v=at:
Ek = 0.5mv2 (Ek : kinetische energie (J)}

Het simulatie proces

Er gaat geen energie verloren (in theorie) maar potentiële- en kinetische energie wisselen elkaar af.
Op het laagste punt is er alleen kinetische energie, op het hoogste punt alleen potentiële.
Daar tussenin bestaat een mix.
Omdat de totale hoeveelheid energie op elk moment gelijk is kunnen we op elk punt de exacte snelheid berekenen.

De richting van de snelheid is loodrecht op de kabel.
De massa wordt versneld door een kracht die ook loodrecht op de kabel staat.
De kracht op de kabel oefent geen energie uit zolang geen uitrekking plaatsvindt.



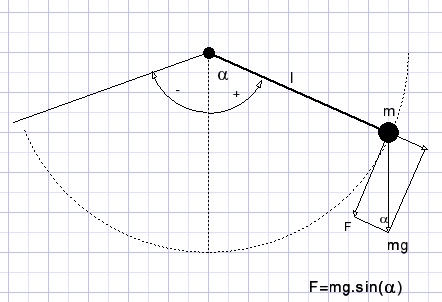
De kracht F hangt af van de hoek α
Meten we α in radialen dan:
    s := αl {s: afstand op de cirkelomtrek, l: kabellengte}
De simulatie is verbazend simpel.
De tijd wordt verdeeld in stukjes van één microseconde.
In deze hele korte tijd doen we of de kracht F en de sneheid v niet veranderen.
F is bekend door de hoek α en veroorzaakt een versnelling van a = F/m = g.sin(α);
De nieuwe snelheid v wordt v + a*10-6.
In deze korte tijd wordt afstand s = v.10-6 afgelegd
en omdat s = αl
wordt de nieuwe hoek α + vt/l.

Na 10000 van deze stapjes wordt een nieuw plaatje getekend.
Dat zijn dus 100 beelden per seconde.

De relatie tussen de snelheid en de hoogte




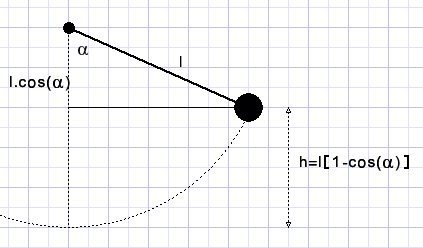
Losgelaten bij een hoek α op h meter boven het laagste punt is de potentiële energie mgh = mgl[1-cos(α)].
Bij een hoek φ is de potentiële energie (verminderd tot) mgl[1-cos(φ)].
Dit energieverlies is kinetische energie geworden zodat:



Het programma gebruikt deze formule om de nauwkeurigheid te controleren:
Bij de maximum snelheid moet de energie gelijk zijn aan de potentiële energie in het bovenste punt.

Een integraal voor de slingertijd

Bij afstandje Δs over de cirkel en snelheid v gedurende hele korte tijd Δt :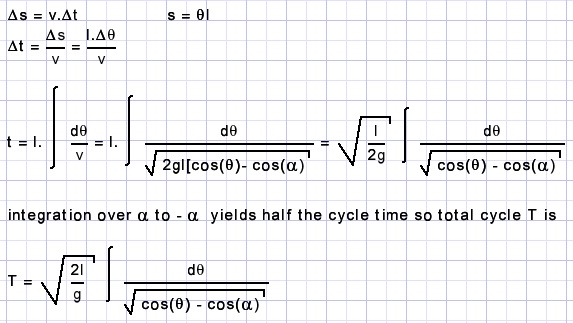



Deze integraal is lastig te bepalen.

Speciaal geval: kleine hoek α

Schrijf cos(x) = 1 - 2sin2(x/2) :
    cos(φ) - cos(α) = 2[sin2(α/2) - sin2(φ/2)]
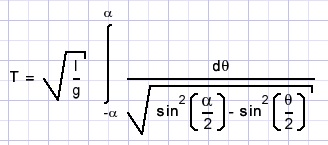
dat verandert de slingertijd integraal naar



Nu substitueren



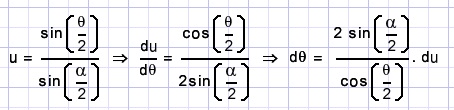
levert op:



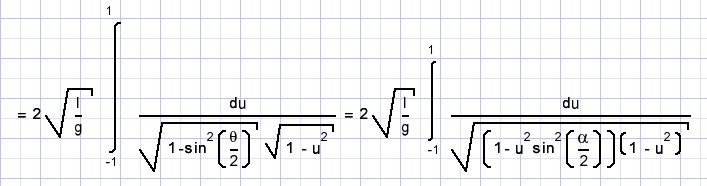
bij kleine α mogen we versimpelen tot



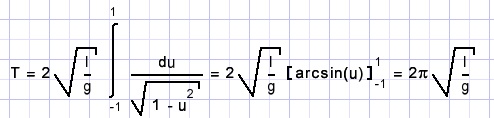
Geïnteresseerd in het Delphi (7) project?
pendule project code

Het programma gebruikt twee eigen componenten:

1. Roterende knop

draaiknop

2. Een microseconden teller:

teller