partities

Een generator van partities

download partitions program

download Delphi-7 project

Een partitie van een (positief,geheel) getal A is een aantal (positief, gehele) getallen die opgeteld A opleveren.
Voorbeeld:
(1,2,3,4) is een partitie van 10 omdat 1+2+3+4 = 10.

Partities komen we tegen bij problemen als:
op hoeveel manieren is een touwtje van 20cm. in vier delen te knippen als elk deel een veelvoud is
van hele cm. en de volgorde er niet toe doet.
Of er is bekend dat de leeftijd van een aantal personen samen 47 jaar is en met nog wat
andere gegevens moeten aan die personen bezigheden worden gekoppeld (zoals bij een logigram).

Dit artikel gaat over een Delphi programma dat systematisch partities genereert.
Die partities zijn te koppelen aan een volgnummer, te beginnen met 0.
Permutaties en combinaties zijn vanuit hun volgnummer direct te berekenen.
Bij partities lukt dat echter niet.
De partitie met volgnummer 3 berekenen lukt alleen vanuit volgnummer 2, die weer vanuit 1.
Om partities te berekenen moeten we weten:

termen

som

Hier volgt een lijst met partities voor SOM = 12 and TERMEN = 4
(het programma in actie)

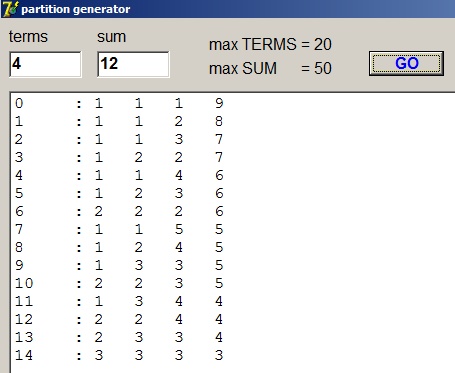
De linker kolom is het volgnummer
De termen zijn van klein naar groot gesorteerd.

Het partitie algoritme

De eerste partitie (nr.0)
Alle kolommen behalve de hoogste krijgen de waarde "1".
De hoogste kolom krijgt waarde SOM - (TERMEN-1).

De partitie volgend op (1,1,1,9)
zie het plaatje hieronder:

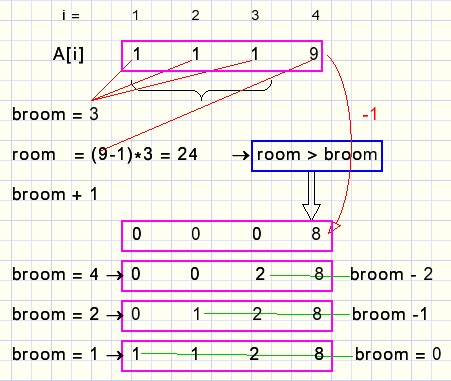
De termen staan in array A[1...maxTERM].
Index variabele i stapt 1,2,3,4.
Waarden A[1],A[2],A[3] worden opgeteld in variabele broom (bezem) die de termen samenveegt.
A[4] verlaagt van 9 naar 8.
Daarna moeten de termen A[1]..A[3] in de beginstand gezet worden.
Dat kan alleen als de broom waarde daarin past.
Met A[4] = 8 is de ruimte (room) van A[1]..A[3] 8*3=24, want er kan maximaal een 8 in.
Met broom = 4 (A[1] + A[2] + A[3] + 1 want A[4]-1),
wordt A[3] = 2, broom wordt 2 (2 minder), A[2] = 1, broom wordt 1 (1 minder), A[1] = broom = 1.

Dit is de algemene regel:

Nog een voorbeeld:
SUM=20, TERMS=5, getoond is rank (volgnummer) 23 en de berekening van rank 24

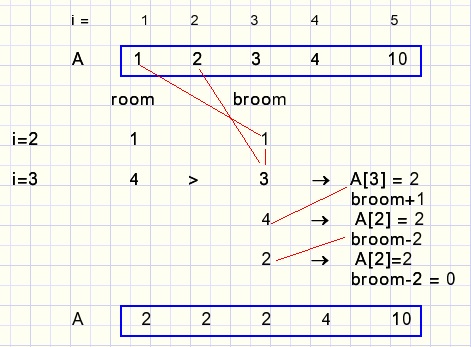
Bij i=3, room=4 omdat A[3] verlaagt naar 2 dus maximaal kan A[1],A[2] = 2 zijn.
room = 2*2 = 4.
broom=3 = A[1] + A[2].
Omdat nu geldt room > broom verlagen we A[3] en resetten termen A[2] en A[1].

Constanten en variabelen:

const maxSUM  = 50;
      maxTERM = 20;

var A : array[1..maxTERM] of byte;
    SUM : byte;
    TERMS : byte;

Deze procedure plaatst de eerste partitie (0):

procedure partition1;
//set 1st partition (#0)
var i : byte;
begin
 for i := 1 to TERMS-1 do A[i] := 1;
 A[TERMS] := SUM - (TERMS-1);
end;

Deze functie berekent de volgende partitie:

function nextpartition : boolean;
//return false if all done
var i,j : byte;
    broom, room : word;
    up : boolean;
begin
 i := 1;
 up := false;
 broom := A[1];
 repeat
  inc(i);
  room := (A[i]-1)*(i-1);
  if room > broom then
   begin
    dec(A[i]);
    inc(broom);
    j := i-1;
    while broom > 0 do
     begin
      if broom-j >= A[j+1] then A[j] := A[j+1]
        else A[j] := broom - (j-1);
      broom := broom - A[j];
      dec(j);
     end;//while
    up := true;
   end
   else broom := broom + A[i];
 until up or (i = TERMS);
 result := up;
end;

Na de laatste partitie exit de functie met false result.

Voor meer details verwijs ik naar de source code.