Parabolische Spiegels

Inleiding
Dit artikel beschrijft de theorie van parabolische spiegels.

De vorm van de gebogen oppervlakte is zodanig, dat recht invallend licht of radiogolven
wordt weerkaatst door één punt, het brandpunt.

Omgekeerd, als in het brandpunt licht of een radiosignaal wordt uitgezonden, dan zal de spiegel
de straling weerkaatsen en als een evenwijdige bundel uitzenden.
Hierboven zie je een voorbeeld van een spiegel als verwarmingselement.

En hieronder een zonnecentrale met parabolische trogspiegels:
Het zonlicht wordt geconcentreerd op een rechte leiding met water of olie.
Met de opgewekte stoom worden turbines aangedreven voor de opwekking van elektriciteit.

Parabolische spiegels treffen we ook aan bij schotelantennes, radarschermen en telescopen.

De theorie
Bekijk eens de figuur hieronder:
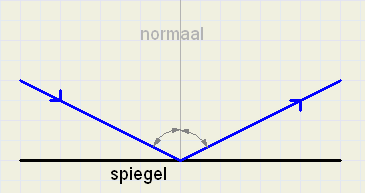Een lichtstraal treft een spiegel en wordt teruggekaatst.
De lijn loodrecht op het spiegelende oppervlak wordt de normaal genoemd.
Het is een natuurkundige wet, dat de hoek van de invallende straal met de normaal gelijk is aan de
hoek van de teruggekaatste straal met die normaal.

In het geval van gebogen oppervlakten is een zeer klein stukje van de speigel als recht te beschouwen
en de normaal staat dan loodrecht op de raaklijn in het betreffende punt.

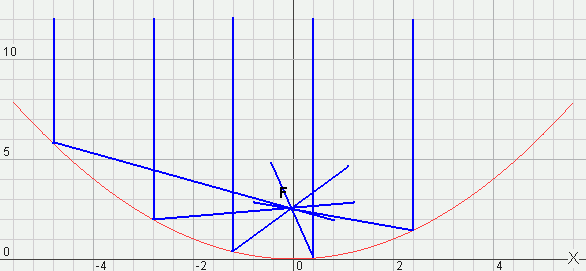Hierboven is in rood een parabool getekend.
Alleen de vertikaal invallende lichtstralen (blauw) gaan door het brandpunt F.
Andersom: vanuit F uitgezonden licht zal na weerkaatsing door de spiegel als een rechte
bundel worden uitgezonden.

Het spiegelende oppervlak heeft de vorm van een parabool.
De grafiek van een parabool wordt gevormd door alle punten die gelijke afstand hebben tot
een punt (brandpunt) en een lijn (richtlijn) .
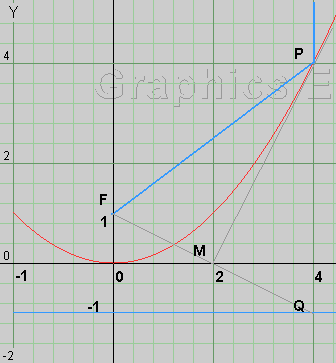In de figuur hierboven heeft het brandpunt F coördinaten (0,1),
de richtlijn heeft als vergelijking y = -1

Voor elk punt P geldt, dat PF = PQ, waarbij Q op de richtlijn ligt, loodrecht onder P.

We berekenen nu de vergelijking van de parabool.
Neem aan, dat P coördinaten (x,y) heeft, dan geldt (Pythagoras) :
    PF2 = x2 + (y-1)2
    en ook
    PQ = y + 1
    en wegens PF = PQ:
    (y+1)2 = x2 + (y-1)2
    y2 + 2y + 1 = x2 + y2 -2y + 1
    4y = x2
    y = 0,25.x2
De vraag is nu, waarom een loodrecht invallende lichtstraal wordt weerkaatst door het brandpunt F.
Beschouw in de figuur hierboven de gelijkbenige driehoek FPQ.
M is het midden van FQ en zal, wegens gelijkvormigheid, op de x-as liggen.
We stellen de vergelijking op van de lijn MP en tonen daarna aan, dat deze de parabool raakt.
We geven punt P even de coördinaten (h,v)
    richtingcoëfficient (rc) van FQ =
    −2
    h
    zodat rc. van MP =
    h
    2
    coördinaten van M zijn (
    h
    2
    ,0) dus vergelijking MP wordt y = 
    h
    2
     
    æx − 
    h
    2
    		ö
    ­­
    èø
    voor het snijpunt met y = 
    x 2
    4
     geldt:
    x 2
    4
     = 
    h
    2
     
    æx − 
    h
    2
    		ö
    ­­
    èø
    x 2
    4
     = 
    h x
    2
     − 
    h 2
    4
     en
    x 2 = 2 h x − h 2
    x 2 − 2 h x + h 2 = 0
    (x − h) 2 = 0
    x = h
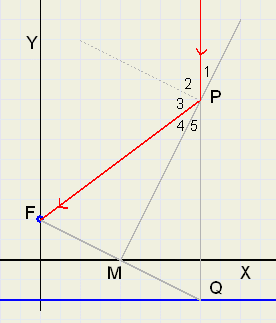
Er is dus maar één snijpunt, zodat MP inderdaad de raaklijn aan de parabool is.

Bekijk nu de volgende figuur:
hierin is
    LP1 = LP5 ................{x hoeken}
    LP4 = LP5 ................{middelloodlijn gelijkbenige driehoek FQP deelt tophoek}
    zodat
    LP1 = LP4
    omdat
    LP12 = LP34 = 900 is dus ook
    LP2 = LP3
Hiermee is het bewijs geleverd.
Elke vertikaal invallende straal zal, omgebogen, door het brandpunt F gaan.

Opgave
Bereken de vergelijking van een parabool met brandpunt F(0,p) en richtlijn y = q.