afstand tussen parabolen

de afstand tussen twee parabolen

Het volgende problem werd in de Facebook groep "Matematica" gepost door Omid Motahed,
wiskunde docent te Beying.

Gegeven zijn twee parabolen.
Vind punten A en B zodat de afstand AB minimaal is.
Zie onderstaande figuur:

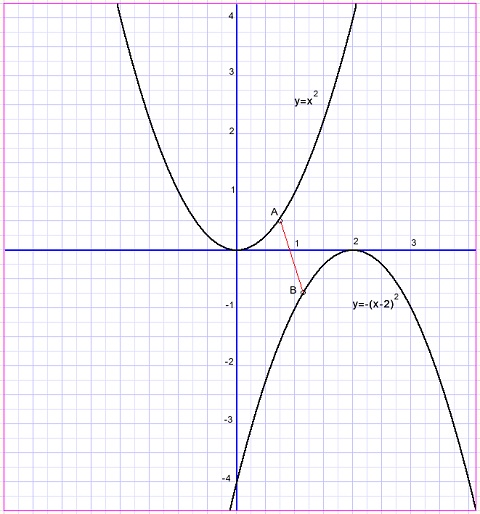
Twee manieren staan open:

1. De numerieke oplossing

Dit was iets lastiger dan gedacht door de twee variable punten A en B.
Na een paar valse starts rolde dit algoritme eruit:

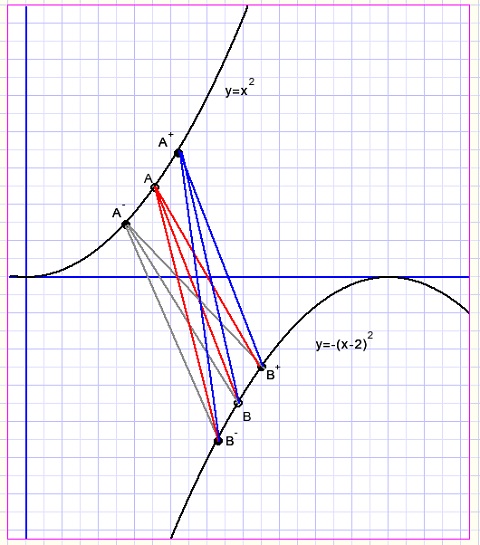
Punten A en B worden enigszins willekeurig gekozen, afstand AB wordt berekend.
Alternatieve punten A⁺ en A^- liggen op korte afstand van A.
Voor B geldt eenzelfde aanpak met dezelfde afstanden.
Kies nu de kortste afstand AB^-.....A⁺B⁺.
Vervang AB als een andere afstand korter is.
Halveer de stapgrootte als AB niet werd vervangen
Herhaal deze procedure totdat de stapgrootte heel klein is geworden.

Het Delphi programma

 type TDistance = record
                  x1 : single;//A
                  y1 : single;
                  x2 : single;//B
                  y2 : single;
                  D  : single;//squared distance AB
                end;
				
				
var DD : array[0..8] of TDistance;

Array DD bevat de coördinaten van A(x1,y1) , B(x2,y2) en de afstand D = AB.
Er is één repeat...until loop waarin alle 9 afstanden worden berekend.
DD[0] bevat AB en wordt vervangen door DD[n] als die een kleinere D waarde heeft.

Ziehier het resultaat:

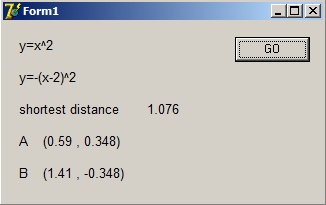
Klik [hier] om het hele Delphi-7 te openen.

De analytische oplossing

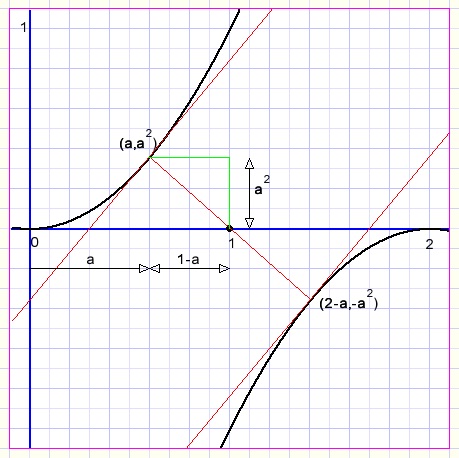
Eerst kiezen we A(a,a²) op parabool y = x².
In dit punt is de richtingscoëfficient van de raaklijn 2a.
De raaklijn van parabool y = -(x-2)² heeft in punt B(2-a,-a²) dezelfde richtingscoëfficient.
Lijn AB gaat door punt (1,0) wegens symmetrie.
In het geval van de kortste afstand zal AB loodrecht op de raaklijnen staan.
Het product van de richtingscoëfficienten is dan gelijk -1.

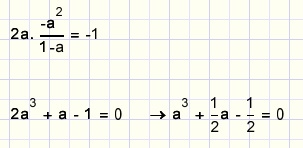
De algemene oplossing van dit type derdemachts vergelijkingen is:

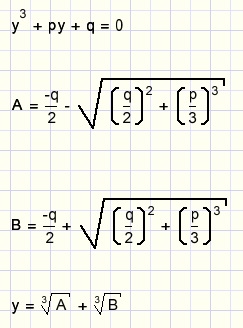
Het bewijs vermeld ik hier niet.
Voor p=0.5 en q=-0.5 vinden we: