Een paden probleem

download Path program

download Delphi project

In de Facebook groep “Classical Mathematics” vond ik het volgende probleem:

Tel het aantal paden van A naar B in de volgende figuur.
De paden mogen elkaar niet raken en moeten (horizontaal of vertikaal) door elk vierkant gaan.

Een van die paden is hieronder aangegeven:

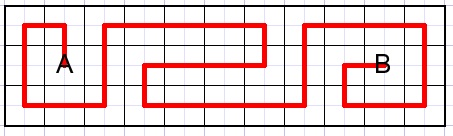
De puzzel hiervoor telt 11 kolommen en 3 rijen.
Om dit probleem aan te pakken is het handig eerst van minder kolommen uit te gaan.
Daarom een programma geschreven dat de paden telt in figuren van 4 tot 15 kolommen.

Zo ziet het programma er uit:

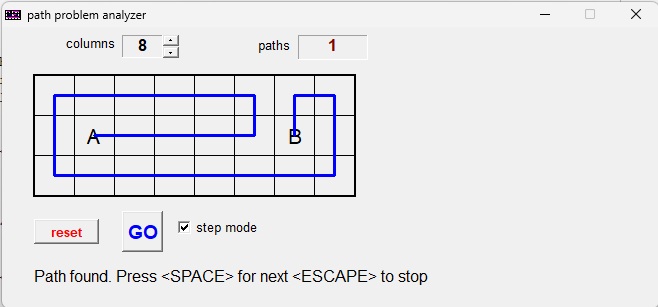
Getoond wordt het eerst gevonden pad in een figuur met 8 kolommen.

Het zoekproces start door op de GO knop te klikken.
Druk op de SPACE bar om meer paden te vinden.
In de STEP modus wordt elk pad getoond.
Als STEPmodus niet is aangevinkt dan telt de computer alleen de paden maar toont niets.

Programma beschrijving

Dit programma is geschreven in de taal Delphi (7).
Vierkantjes zijn genummerd zoals hieronder aangegeven (voor een 11 kolommen puzzel):

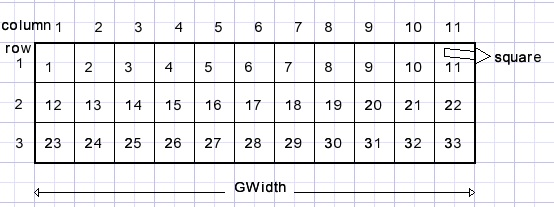
Een pad wordt geregistreerd in array paths[ ] als opvolgend vierkantje..richting, vierkantje richting...
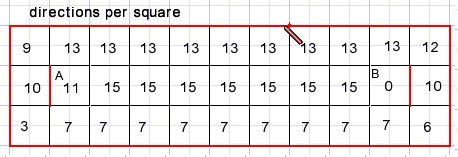
A is het beginpunt (13) ,B het eindpunt (21).

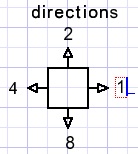
Bij elk vierkantje (square) is er een getal dirs dat aangeeft in welke richtingen (1,2,4,8) een pad mag lopen:
(rode lijnen mogen niet gekruist worden)

Data formats

type Tsquare = record
                col : byte;      //column of square
                row : byte;      //row ..
                dirs : byte;     //allowed entry/exit directions
                                 //1:right; 2:up; 4:left; 8:down
                full : boolean;  //path present
               end;
     TsearchResult = (srStart,srCnt,srOK,srEnd);
     Tstep = record
              pos : byte;        //place of square
              dir : byte;        //direction 1,2,4,8
             end;

var bm : Tbitmap;
    square : array[1..45] of Tsquare; //directions, col, row,                
                                      // pah preset
    Gwidth : byte = 4;                //number of columns   

//-- path finding --

    path : array[1..45] of Tstep;     //square and direction per                 
                                      //step
    pathlength : byte;
    pathcount  : longword;
    search     : TsearchResult;
    squareA    : byte;
    squareB    : byte;
    searchBusy : boolean;

Functies en procedures

procedure setDimension;

Tekenen van de puzzel gebeurt in bitmap BM, die naar form1.paintbox1 wordt gekopieerd.
Dat voorkomt naar geknipper. De paintbox wordt nooit gewist maar alleen overschreven.
setDimension wist een deel van het form1.canvas om een paintbox met nieuwe afmetingen weer te geven.
Geeft in array square[ ] de waarden van de rij,kolom en dirs
Geeft waarde van Gwidth (aantal kolommen) en pathlength = 3*Gwidth.

procedure clearPath;

Wist het Path[ ] array waarin oud pad staat. Zet de full flag op false in array square[ ]

procedure procSearch;

Controleert het zoekproces naar nieuwe paden.
Roept aan functie findPath(sr) : Tsearchresult;

Tsearchresult : srStart : zoek eerste pad (parameter)
                srOK    : pad gevonden (result)
                srCnt   : zoek volgend pad (paramameter)
                srEnd   : geen pad gevonden (result)
				
function findpath(sr : TsearchResult) : Tsearchresult;
label nextstep,teststep,nextdirection,stepBack;
var xdir,nextpos,xpos,step : byte;

Deze functie zoekt naar een pad.
Xdir : huidige zoekrichting
Xpos : huidige vierkantje
nextpos : mogelijk volgend vierkantje
step : verhoogt bij elke nieuwe stap (vierkantje), is index in path[ ] array.

Of een richting mogelijk is vanuit een vierkantje zien we zo:

if (square[xpos].dirs and xdir) = 0 then goto nextdirection;

Of een vierkantje reeds een pad bevat:

if square[nextpos].full then goto nextdirection;

De dirs velden van path[ ] vormen een telwerk. Door systematisch te tellen missen we geen pad.
Per vierkantje Xpos tellen we 1..2..4..8
Als richting Xdir is toegstaan en het vierkantje nextpos geen pad bevat dat wordt de stap geregistreerd in path[ ]:

path[step].dir := xdir;
inc(step);
path[step].pos := nextpos;
xpos := nextpos;
square[xpos].full := true;

Als geen stap mogelijk is dan gaan we een stap terug en proberen een volgende richting:

if step = 1 then
  begin
   result := srEnd;  //no path found
   exit;
  end;
 square[xpos].full := false;
 dec(step);
 xpos := path[step].pos;
 xdir := path[step].dir;
 goto nextdirection;
end;

next direction code is:

xdir := xdir shl 1;
if xdir > 8 then goto stepback;
goto teststep;

Search flowchart

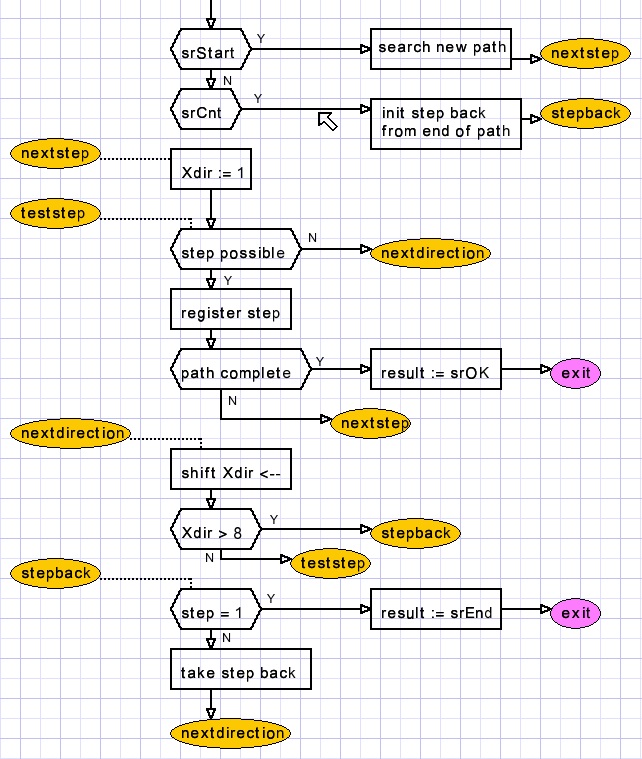
Zie de source code voor details.

Resultaten

columns	4	5	6	7	8	9	10	11	12
paths	2	6	14	30	62	126	254	510	1022
path+2	4	8	16	32	64	128	256	512	1024
(path+2)/2^(n-2)	1	1	1	1	1	1	1	1	1

So:

Deze formule P(n) voor het aantal paden bij n kolommen is geldig voor zeker n=4..12
Maar absolute zekerheid is er niet voor n=13,14....

Analyse

Om het wat eenvoudiger te maken halveren we het aantal paden door in vierkantje 2
alleen de richting naar rechts toe te staan.
Lila lijnen verdelen de figuur vervolgens in secties.
De zoektocht gaat uit van de richting naar rechts.

4 Kolommen

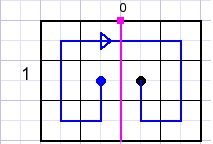
1 pad gevonden.
De lila lijn verdeelt de puzzel in twee secties maar dit heeft geen effect.

5 kolommen

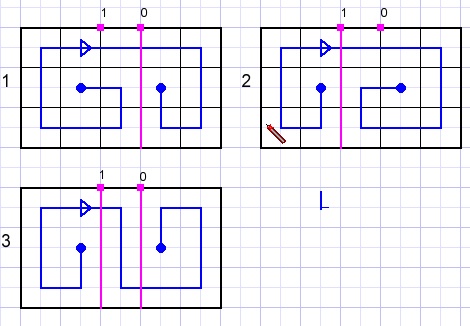
Drie paden.
Twee lila lijnen zijn mogelijk. Geen lijn heeft hetzelfde effect als lijn 1 (bit 0 = 1)

6 kolommen

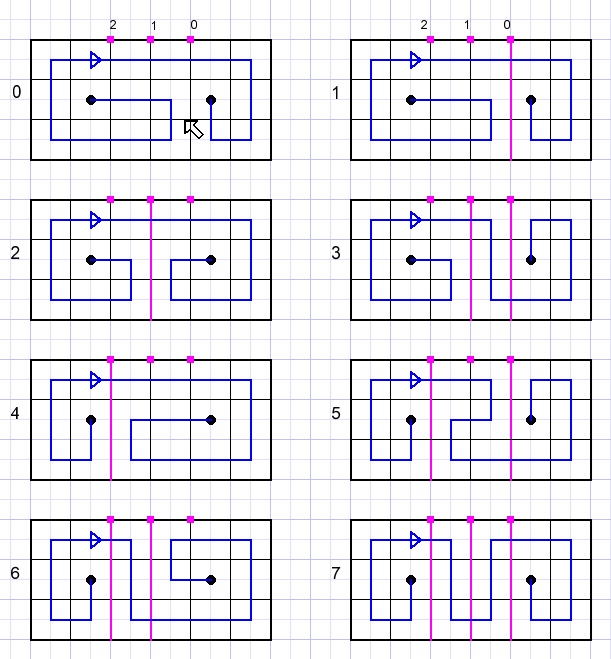
7 paden gevonden.
Opmerking: paden 0 en 1 zijn gelijk.

Conclusie

In een n kolommen puzzel zijn n-3 lijnen te trekken die de puzzel in secties verdelen.
Die lijnen zijn te plaatsen op 2^(n-3)-1 manieren.

Regel: verlaat geen sectie zolang niet alle vierkantjes doorkruist zijn.

Als P(n) het aantal paden is voor een n kolommen puzzel dan
(nu wel de richting links toestaan in vierkant 2 wat de paden verdubbelt)