Oversteek

Downloads:

rivercross1 programma

rivercross2 programma

rivercross1 source listing

rivercross2 source liesting

rivercross1 Delphi-7 project

rivercross2 Delphi-7 project

Introductie

In dit artikel beschrijf ik twee klassieke puzzels die sterk op elkaar lijken en
twee Delphi programmas die de oplossing zoeken.
Die Delphi projecten heten rivercross1 en rivercross2.
(1) Is het probleem van een boer die een geit, een kool en een wolf naar de overkant
van een rivier moet roeien.
De boot biedt naast de boer plaats voor één object.
De geit en de kool mogen niet onbewaakt achterblijven want dan eet de geit de kool op.
Ook de geit en de wolf mogen niet zonder aanwezigheid van de boer samen zijn om voor de hand liggende reden.

(2) Is het jaloerse echtgenoten probleem.
Drie stellen moeten een rivier oversteken met een roeibootje.
Daar passen maar twee personen in.
Zowel de mannen als de vrouwen kunnen roeien.
Het probleem is dat de mannen zeer jaloers zijn en niet toestaan dat hun vrouw in aanwezigheid
van een andere man verkeert zonder dat ze er zelf bij zijn.
Zelfs niet als van die andere man de vrouw ook aanwezig is.

Het eerste probleem is relatief simpel.
Het tweede is een stuk lastiger.

Maar de manier van oplossen en de programmas zijn vrijwel gelijk.
Er is alleen verschil tussen een paar tabellen.
Daarom leg ik eerst (1) uit en daarna alleen de verschillen met (2).
De nadruk ligt daarbij op het zoekalgoritme.
Resultaten worden simpelweg getoond met een lijstje letters.
Ik heb geen pogingen ondernomen voor een mooie grafische weergave.

Rivercross 1

Programmeren is het schrijven van procedures en functies die data structuren manipuleren.
Welke gegevens zijn er nodig?
De te verplaatsen objecten zijn de boer (F) die moet roeien, de kool (C), de geit (G) en de wolf (W).
Hun positie is op de linker- of de rechteroever van de rivier.
Per object hebben we dus aan één bit genoeg om die positie aan te geven 0: linkeroever 1: rechteroever.
Om van oever te wisselen volstaat de logische bewerking xor 1
Variabele situation bits 0..3 bevatten de positie van elk object:

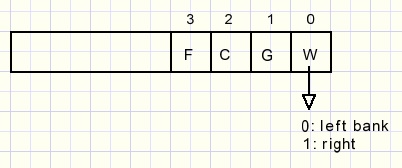
De situatie (positie van de 4 objecten) loopt van 0 tot 15 {15 = (1 shl 4) - 1}

Per overtocht bevat het bootje:

ActionCode[0..4] array heeft de (binaire) waarden voor elke oversteek:

We moeten een lijstje bijhouden van ondernomen akties.
Het crossList[1..20] array doet dat, de aktiecodes zijn 0..4.
We staan maximaal 20 oversteken toe om een oplossing te vinden.

Variabele crossNr is het nummer van de overtocht: 1,2,3....
Oneven oversteken zijn naar de andere oever, de even oversteken zijn terugtochten.
Er is geen noodzaak om voor de richting een speciale variabele in het leven te roepen.

Sommige situaties zijn niet toegestaan, zoals 0000 0110 wat betekent dat de
geit en de kool zonder aanwezigheid van de boer samen zijn op de rechteroever.
Procedure generateLegals genereert een boolean array genaamd legal.
Dat bevat voor elke situatie true of false.

procedure generateLegals;
//fill legal array with false or true values
var i : byte;
    ill,F,C,G,W,NF,NC,NG,NW : boolean;
begin
 for i := 0 to maxSit do
  begin
   F := (i and $8) > 0;
   NF := not F;
   C := (i and $4) > 0;
   NC := not C;
   G := (i and $2) > 0;
   NG := not G;
   W := (i and $1) > 0;
   NW := not W;
   ill := NF and ((C and G) or (G and W));
   if ill = false then
    ill := F and ((NC and NG) or (NG and NW));
   legal[i] := not ill;
  end;
end;

Gedurende de overtochten verdwijnt niemand zodat het gevaar aanwezig is dat oeverloos
heen en weer geroeid wordt.
Om dit te vermijden moeten we eerdere situataties herkennen.
Opnieuw is er een boolean array history[0..15] met true of false per situatie:
false als nog niet bereikt, true als deze situatie eerder optrad.

De oplossing van deze puzzel is de lijst aktiecodes (1..4) in array crossList[ ].
CrossList is eigenlijk een telwerk.
Opmerking:
verwar niet de termen action en actioncode.
action telt 1,2,3,4,1,2,3,4,... en de actioncode[action] verschaft de bitwaarden voor de xor
met de situatie.
Beginnend bevat crossList de waarden (0 0 0 0 0 0 0 0 0 0 0...) als nog geen aktie plaatsvond.
crossNr = 0. situation = 0.
Als boer en geit oversteken: crossNr = 1 en crossList[ ] = (1 0 0 0 0 0 ....) .
Nieuwe situatie wordt 0000 0000 xor 0000 1010 = 0000 1010.
Als de boer terugroeit:
crossNr = 2; situation = 0000 1010 xor 0000 1000 = 0000 0010
crossList[ ] = (1,4,0,0...).
De puzzel is opgelost als situatie 15 (binair 1111) wordt bereikt : iedereen aan de overkant.

De aktiecodes worden in array actionCode gezet:

procedure generateActionCodes;
var i : byte;
begin
 actionCode[0] := 0;
 for i := 1 to 3 do actionCode[i] := $8 or (1 shl (3-i));
 actionCode[4] := $8;
 maxActionCode := 4;
end;

Elke oversteek moet tevoren worden getest:

function crossOK(ac,nr : byte) : boolean;
levert true als aktie ac voor oversteek nr is toegestaan.

function crossOK(ac,nr : byte) : boolean;
//return true if action ac is possible
//test FCGW positions, illegal situtions, situation was met before
var pos,newsituation,code : byte;
begin
 code := actioncode[ac];
 pos := situation and code;                    //test items on proper bank
 if (nr and 1) = 1 then result :=  (pos = 0)
  else result := (pos = code);
 newsituation := situation xor code;
 if result then
  result := legal[newsituation];
 if result then result := (history[newsituation] = false);//avoid repetition
end;

De kern van het project is het zoeken naar oplossingen.
Dat doet
function FindSolution(cs : TcrossStatus) : TCrossStatus;
waar crossStatus de waarde csStart heeft of csEND (geen oplossing) of csSolution (wel oplossing).
Hieronder staat de flowchart.
Een blik op de source code kan schokkend zijn voor puristen van zg. gestructureerd programmeren:
er worden labels en goto statements gebruikt.
Reden zijn de kruisende lussen in de code. Met repeat of while loops zouden extra (boolean) variabelen
nodig zijn om die lussen selectief te doorlopen.
Dat levert dan slecht leesbare code op.
Maar als iemand er in slaagt om toch duidelijke code te schrijven
met repeat of while statements, dan hoor ik dat graag.

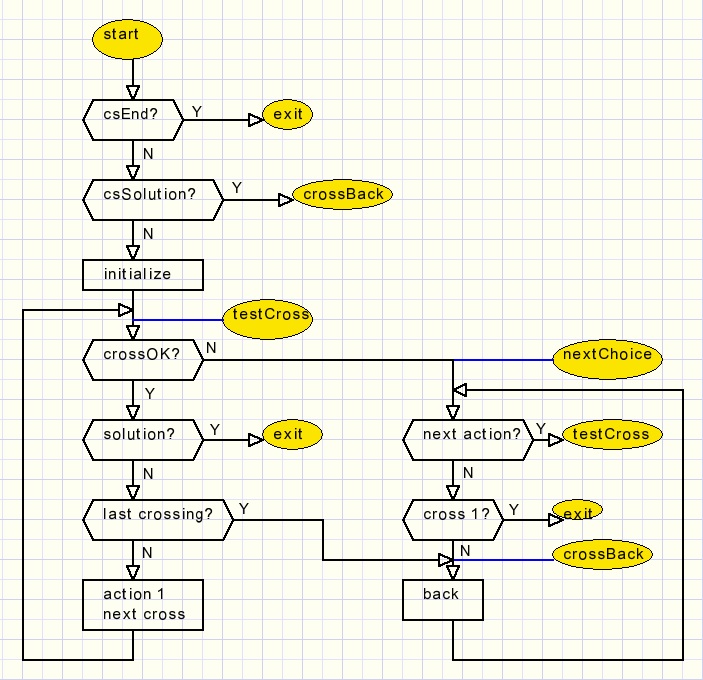
Bekijk de bovenstaande flowchart en de volgende details.
De functie wordt aangeroepen met csStart, csSolution of csEnd.
In geval van csEnd wordt niets gedaan: er zijn geen oplossingen meer.
Bij csSolution gaat de zoektocht verder naar meer oplossingen.
Dat gaat met een sprong naar "crossBack".
Met csStart begint het zoeken naar een eerste oplossing.
Initialisatie:

 crossNr := 1;
 ac := 1;

Als deze aktie OK is dan :

 crossList[crossNr] := ac;
 situation := situation xor actionCode[ac];
 history[situation] := true;

Nu testen of oplossing is bereikt:

  if situation = maxSit then
  begin
   result := csSolution;
   exit;
  end;

Opmerking: maxsit = 15, binair 1111, de maximale situatie.

Indien geen oplossing dan test of maximale oversteek is bereikt:

  if crossNr = maxCross then goto crossBack;

Als er meer oversteken gemaakt mogen worden:

  inc(crossNr);
  ac := 1;
  goto testCross;

De volgende oversteek met de aktieteller op de eerste waarde 1.

Als de aktie niet is toegestaan dan wordt de volgende geprobeerd: (label nextchoice)

 nextChoice:
  if ac < maxActionCode then
  begin
   inc(ac);
   goto  testCross;
  end;

Zijn alle akties zijn geprobeerd dan moet de laatste aktie teruggenomen worden.
Maar oversteek 1 kan niet geannuleerd worden, dat betekent dat er geen oplossing is.

  if crossNr = 1 then
  begin
   result := csEnd;
   exit;
  end;

Niet oversteek 1 en laatste aktie teniet doen:

 history[situation] := false;
 situation := situation xor actionCode[crossList[crossNr]];
 crossList[crossNr] := 0;
 dec(crossNr);

Dit voert ons terug naar de vorige oversteek.

Nu voeren we de code uit na label crossBack
Deze oversteek leidde niet tot resultaat en moet dus geannuleerd worden:

 crossBack:
  history[situation] := false;
  ac := crossList[crossNr];
  situation := situation xor actionCode[ac];
  crossList[crossNr] := 0;
  goto nextChoice;

Een paar opmerkingen bij de functie crossOK die akties test.
De eerste test betreft of de objecten op de goede oever staan:

 code := actioncode[ac];
 pos := situation and code;                    //test items on proper bank
 if (nr and 1) = 1 then result :=  (pos = 0)   //nr is pass number (odd,even)
  else result := (pos = code);

Voor de oversteek naar de andere oever moeten de betreffende bits 0 zijn.
Voor een terugtocht is dat 1.

Dan testen we voor foute situaties:

 newsituation := situation xor code;
 if result then
  result := legal[newsituation];

De laatste test betreft uitsluiten van eerdere situaties om oeverloos heen en weer varen te voorkomen:

 if result then result := (history[newsituation] = false);//avoid repetition

Hieronder een (verkleind) plaatje van het programma met oplossing:

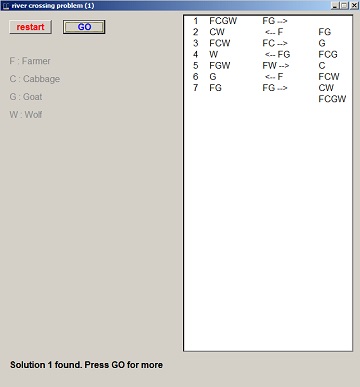
Tot zover rivercross1.

Rivercross2

De verschillen met rivercross1 zijn:

Objecten:

De echtparen noemen we Aa (A man, a vrouw) Bb en Cc.
Er zijn dus 64 situaties: 0 tot 63, binary 000000 tot 111111

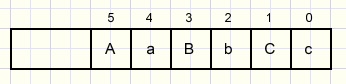
procedure generateLegals zet de waarde true of false in array legal voor elke situatie.

procedure generateLegals;
//set false / true for each situation
var i : byte;
    mA,fA,mB,fB,mC,fC,nmA,nfA,nmB,nfB,nmC,nfC : boolean;
    ill : boolean;
begin
 for i := 0 to maxsit do
  begin
   mA := (i and $20) > 0;  //male A
   nmA := not mA;          //not male A
   fA:= (i and $10) > 0;   //female a
   nfA := not fA;          //not female a
   mB := (i and $8) > 0;
   nmB := not mB;
   fB := (i and $4) > 0;
   nfB := not fB;
   mC := (i and $2) > 0;
   nmC := not mC;
   fC := (i and $1) > 0;
   nfC := not fC;
   ill := (nmA and fA and (mB or mC)) or
          (nmB and fB and (mA or mC)) or
          (nmC and fC and (mA or mB)) or
          (mA and nfA and (nmB or nmC)) or
          (mB and nfB and (nmA or nmC)) or
          (mC and nfC and (nmA or nmB));
   legal[i] := not ill;
  end;
end;

procedure generateActionCodes vult het actionCode array met de akties.
De boot vervoert één of twee personen en combinaties van man uit vrouw van verschillende stellen kunnen niet.
Eerst worden de combinaties van twee personen berekend en daarna de éénpersoons overtochten.

procedure generateActionCodes;
var ac,i,j : byte;
    mA,fA,mB,fB,mC,fC : boolean;
    ill : boolean;
begin
 maxActionCode := 0;
 actionCode[maxActionCode] := 0;
 for i := 1 to 5 do                       //2 passengers actions
  for j := i+1 to 6 do
   begin
    ac := (1 shl (6-i)) or (1 shl (6-j)); //action code
    mA := (ac and $20) > 0;               //male A
    fA := (ac and $10) > 0;               //female a
    mB := (ac and $8)  > 0;
    fB := (ac and $4)  > 0;
    mC := (ac and $2)  > 0;
    fC := (ac and $1)  > 0;
    ill := (mA and (fB or fC)) or         //illegal
           (mB and (fA or fC)) or
           (mC and (fA or fB));
    if ill = false then
     begin
      inc(maxActionCode);
      actionCode[maxActionCode] := ac;
     end;
   end;
 for i := 1 to 6 do                       //1 passenger actions
  begin
   inc(maxActionCode);
   actionCode[maxActionCode] := (1 shl (6-i));
  end;
end;

Een (verkleind) plaatje van het programma met oplossing: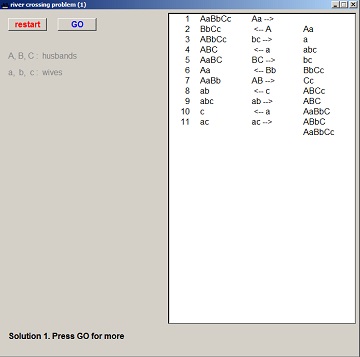

Hierme beëindig ik deze beschrijving van twee klassieke puzzels.