Een numerieke berekening van π

download programma
download Delphi(7) project



De oppervlakte A van de hele cirkel is πr2
Als de straal r=1 dan is dus π =A
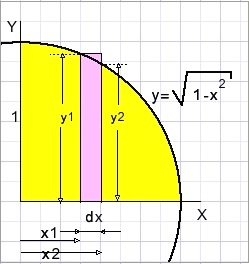
Oppervlakte A bepalen we door een kwart cirkel in vertikale rechthoekige reepje te snijden
en die oppervlaktes op te tellen.
Hoe smaller de reepjes (hoe kleiner dx) hoe nauwkeuriger het antwoord.
We tellen zowel de oppervlaktes y1*dx op (som Aout) als de oppervlaktes y2*dx (som Ain).
De echte oppervlakte ligt ergens tussen A1 en A2 in.



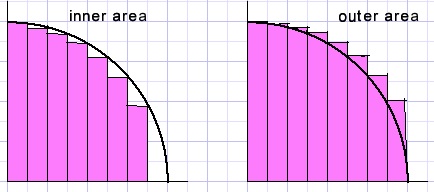
De keuze van dx
Computers rekenen in het tweetallig stelsel.
In dat talstelsel kan je 0,1 niet exact weergeven, zoals 1/3 in het tientallig stelsel altijd een kleine fout zal vertonen.
Getallen in de vorm x/(2^n) zijn wel precies. (x, n zijn natuurlijke getallen)
Goede waardes voor dx zijn daarom ½ ¼ 1/8 1/16 ….. etc.

Het programma



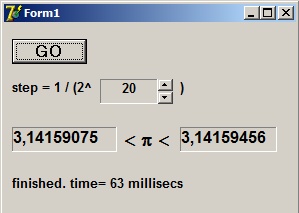
Step is dx.
Een UpDown component selecteert de stapgrootte.
Onder- en bovengrens van π wordt getoond.
Deze procedure wordt door de GO button gestart:

procedure TForm1.Button1Click(Sender: TObject);
var dx : double;
    i : byte;
    Ain,Aout,x1,x2,y1,y2 : double;
    t1,t2 : longword;
begin
 label4.Caption := 'busy';
 statictext1.Caption := '';
 statictext2.Caption := '';
 application.ProcessMessages;
 t1 := gettickcount;
 dx := 1;
 for i := 1 to UpDown1.position do dx := dx *0.5;//make dx
 x1 := 0;
 y1 := 1;
 Ain := 0;   //inner area
 Aout := 0;  //outer area
 while x1 < 1 do
  begin
   x2 := x1+dx;
   y2 := sqrt(1-sqr(x2));
   Aout := Aout + dx*y1;
   Ain := Ain + dx*y2;
   x1 := x2;
   y1 := y2;
  end;
 Aout := Aout*4; //complete circle
 Ain := Ain*4;
 statictext1.Caption := formatfloat('0.00000000',Ain);
 statictext2.Caption := formatfloat('0.00000000',Aout);
 t2 := gettickcount;
 label4.Caption := 'finished. time= '+inttostr(t2-t1)+ ' millisecs';
end;
Selecteer andere waarden van dx en zie het verschil in nauwkeurigheid.