

 |
het 12 munten probleem |  |
 |
In een zak bevinden zich 12 munten, die er hetzelfde uitzien.
Maar bekend is dat er mogelijk één munt bij is, die lichter of zwaarder is dan de andere.
Ook is er een balans met aan elke kant een schaaltje waarmee de munten te wegen, dus te vergelijken, zijn.
Hoeveel wegingen zijn er nodig om die mogelijk afwijkende munt te vinden?
En in het algemeen:
-
- uit hoeveel munten m kunnen we een afwijkende munt vinden als er w wegingen plaatsvinden?
Codering van wegingen
Zie figuur hieronder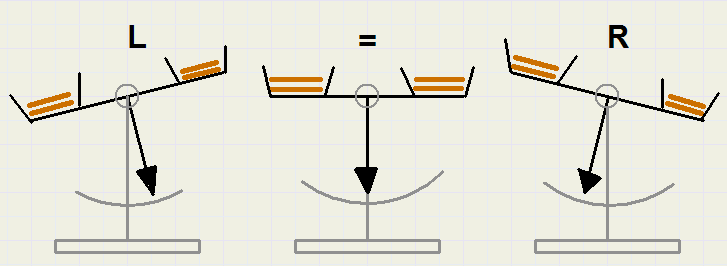
Merk op, dat
-
"L" betekent dat links de zwaardere of rechts de lichtere munt ligt.
"=" betekent dat alle munten gelijk zijn
"R" betekent dat links de lichtere- of rechts de zwaardere munt ligt.
Twee wegingen
We tellen in de volgorde "L" , "=" , "R" en van links naar rechts.| weging 1 | weging 2 |
| L | L |
| = | L |
| R | L |
| L | = |
| = | = |
| R | = |
| L | R |
| = | R |
| R | R |
Stel , dat wegingen "LL" hoort bij de situatie "munt 1 zwaarder". Dan hoort "RR" bij "munt 1 lichter".
Bij 2 wegingen zijn er 32 regels, waarvan één gelijk is aan "==" .
Het lijkt er dus op, dat met 2 wegingen een afwijkende munt uit (32 - 1) / 2 = 4 kan worden gevonden.
De regels 1...4 van de tabel zijn te koppelen aan munt 1..4 afwijkend.
Maar bekijk eens van regels 1...4 de linker kolom van de tabel: daar staat .........L = R L ...........3 letters.
Een letter (L of R) betekent dat de munt die aan die regel is gekoppeld aan de weging moet deelnemen.
Maar 3 munten zijn niet over twee schaaltjes te verdelen.
Daarom laten we wegingen "LL" en "RR" niet meedoen.
De tabel passen we wat aan:
| afwijkende munt | weging 1 | weging 2 |
| 1 | = | L |
| 2 | R | L |
| 3 | L | = |
| 3 | R | = |
| 2 | L | R |
| 1 | = | R |
Alleen staat nog niet vast hoe de munten per weging over de schaaltjes verdeeld moeten worden.
Laten we de munten om en om op het linker en rechter schaaltje leggen.
| munt | afwijking | weging 1 | weging 2 |
| 1 | + | = | L |
| 2 | - | R | L |
| 3 | - | L | = |
| 3 | + | R | = |
| 2 | + | L | R |
| 1 | - | = | R |
-
"=" : munt doet niet mee aan weging
"L" uitslag links geplaatst of "R" uitslag rechtsgeplaatst : munt zwaarder
"L" uitslag rechts geplaatst of "R" uitslag linksgeplaatst : munt lichter
Het algemene geval voor w wegingen en m munten.
w wegingen leveren 3w combinaties op van de tekens "L" , "=" , en "R".De weging "===" staat voor "alle munten gelijk".
Per kolom van de tabel komen alle tekens (L=R) even vaak voor.
Er zijn dus per kolom 3w - (3w / 3) = 2.3w-1tekens "L" of "R"
De ene helft van die regels hoort bij "munt i zwaarder" , de andere helft bij "munt i lichter".
Zodat er per weging 3w-1 munten over de twee schaaltjes verdeeld moeten worden.
Maar dat is niet mogelijk omdat het een oneven aantal is.
Daarom laten we de combinaties "LL...LL" en dus ook "RR...RR" niet meedoen.
Daardoor zijn er nu 2.3w-1 - 2 = 2(3w-1 -1) letters per kolom,
dus per weging moeten (3w-1 -1) munten over de schaaltjes worden verdeeld.
Dat is altijd een even aantal, dus geen probleem.
Bij w wegingen kunnen we een afwijkende munt vinden uit m = (3w - 3)/2 munten.
Per weging liggen er per schaaltje (3w-1 -1) / 2 munten
Drie wegingen en 12 munten
Bij 3 wegingen is m = 3(3-1) - 1 = 12, uit 12 munten kan één mogelijk afwijkende munt worden bepaald.We maken een tabel als hierboven en vullen eerst in de kolommen "munt" , "weging 1" , "weging 2" en "weging 3".
Merk op, dat de regels met de uitslagen "LLL" , "===" , en "RRR" zijn weggelaten.
Omdat in de kolom van weging 3 de eerste 8 munten uitslag "L" hebben, nemen we afwisselend een + en een - afwijking
hebben voor een gelijke verdeling van de munten over de schaaltjes.
| munt | afwijking | weging 1 | weging 2 | weging 3 |
| 1 | + | = | L | L |
| 2 | - | R | L | L |
| 3 | + | L | = | L |
| 4 | - | = | = | L |
| 5 | + | R | = | L |
| 6 | - | L | R | L |
| 7 | + | = | R | L |
| 8 | - | R | R | L |
| 9 | + | L | L | = |
| 10 | - | = | L | = |
| 11 | + | R | L | = |
| 12 | - | L | = | = |
| 12 | + | R | = | = |
| 11 | - | L | R | = |
| 10 | + | = | R | = |
| 9 | - | R | R | = |
| 8 | + | L | L | R |
| 7 | - | = | L | R |
| 6 | + | R | L | R |
| 5 | - | L | = | R |
| 4 | + | = | = | R |
| 3 | - | R | = | R |
| 2 | + | L | R | R |
| 1 | - | = | R | R |
Merk op:
-
+ L en - R : linkerschaaltje
- L en + R : rechterschaaltje
"- " betekent dat de munt niet deelneemt aan de weging.
Plaatsingstabel:
| munt | weging 1 schaal | weging 2 schaal | weging 3 schaal |
| 1 | - | L | L |
| 2 | L | R | R |
| 3 | L | - | L |
| 4 | - | - | R |
| 5 | R | - | L |
| 6 | R | L | R |
| 7 | - | R | L |
| 8 | L | L | R |
| 9 | L | L | - |
| 10 | - | R | - |
| 11 | R | L | - |
| 12 | R | - | - |
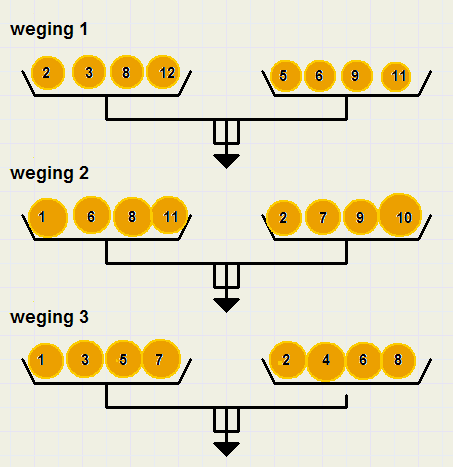
...weging 1:.........LLRRLLRR.........{4 maal linkerschaal en 4 keer rechterschaal, OK}
...weging 2:.........LRLRLLRL..........{5 maal linkerschaal en 3 keer rechterschaal, fout}
...weging 3:.........LRLRLRLR.........{4 maal linkerschaal en 4 keer rechterschaal, OK}
We moeten voor weging 2 een munt van het linker- naar het rechterschaaltje verplaatsen, zonder de andere metingen
te beïnvloeden.
Dat kan door de "+" en "-" afwijking van munten 9 en 12 te verwisselen.
Kolom 1 behoudt dan evenveel "L" als "R" voor de schaaltjes en kolom 2 verplaatst een munt naar het rechterschaaltje.
De plaatsingtabel wordt hiermee:
| munt | weging 1 schaal | weging 2 schaal | weging 3 schaal |
| 1 | - | L | L |
| 2 | L | R | R |
| 3 | L | - | L |
| 4 | - | - | R |
| 5 | R | - | L |
| 6 | R | L | R |
| 7 | - | R | L |
| 8 | L | L | R |
| 9 | R | R | - |
| 10 | - | R | - |
| 11 | R | L | - |
| 12 | L | - | - |
De oorspronkelijke wegingentabel ziet er nu zo uit:
| munt | afwijking | weging 1 | weging 2 | weging 3 |
| 1 | + | = | L | L |
| 2 | - | R | L | L |
| 3 | + | L | = | L |
| 4 | - | = | = | L |
| 5 | + | R | = | L |
| 6 | - | L | R | L |
| 7 | + | = | R | L |
| 8 | - | R | R | L |
| 9 | - | L | L | = |
| 10 | - | = | L | = |
| 11 | + | R | L | = |
| 12 | + | L | = | = |
| 12 | - | R | = | = |
| 11 | - | L | R | = |
| 10 | + | = | R | = |
| 9 | + | R | R | = |
| 8 | + | L | L | R |
| 7 | - | = | L | R |
| 6 | + | R | L | R |
| 5 | - | L | = | R |
| 4 | + | = | = | R |
| 3 | - | R | = | R |
| 2 | + | L | R | R |
| 1 | - | = | R | R |
Resteert nog een manier om vooraf door berekening het schaaltje van een munt per weging te bepalen.
Mooie toepassing van de lineaire algebra?


