

| De Stellingen van Menelaos en Ceva |  |
Menelaos
Zie de volgende figuur:Driehoek ABC wordt doorsneden door een lijn door de punten P,Q,R:
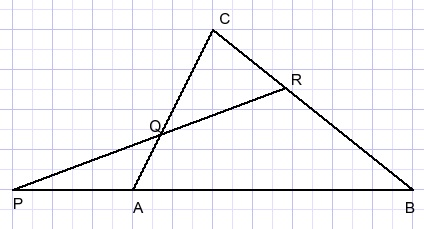
De stelling van Menelaos luidt:
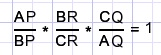
Bewijs
Trek loodlijnen: A-->A' B-->B' en C-->C'
Dat levert gelijkvormige driehoeken AA'Q en CC'Q , CC'R en BB'R , AA'P en BB'P
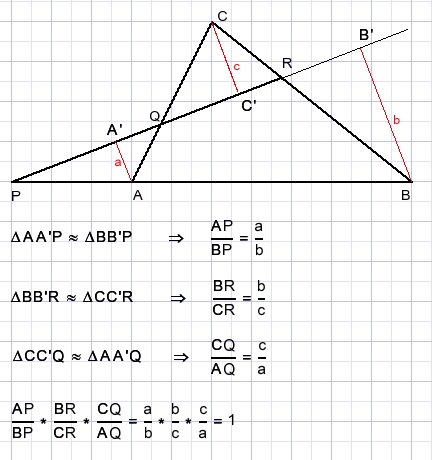
Omgekeerd
Als het product van de lijnstukken 1 is, dan liggen de punten P,Q,R op één lijn.
Het bewijs geef ik hier niet.
Systematische aanpak
Loop over de omtrek van driehoek ABC tegen de klok in.
Dat gaat over de zijden AB, BC en CA.
Schrijf in geval van AB A als de teller en B als de noemer van een breuk, evenzo voor BC en CA:
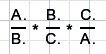
Bij AB is P het snijpunt, vul voor de punt A./B. de P in.
Vul bij de punt van B./C. de R in van het snijpunt.
Vul bij de punt C./A. de Q in van het snijpunt.
Ceva
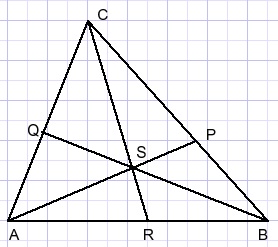
Als de drie lijnen door de hoekpunten van een driehoek (ABC) door één punt (S) gaan geldt:
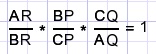
Dit is de stelling van Ceva.
Bewijs
We maken gebruik van de stelling van Menelaos.
Bekijk de driehoek ARC met snijlijn BQ en ook driehoek RBC met snijlijn AP.
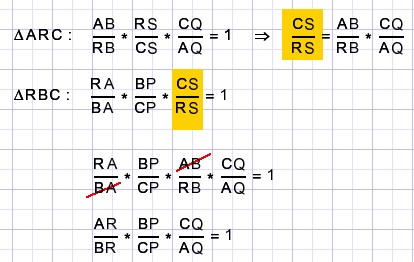
Omgekeerd
Als het product 1 is dan gaan de lijnen (door A,B,C) door één punt.
De sinusstelling van Ceva
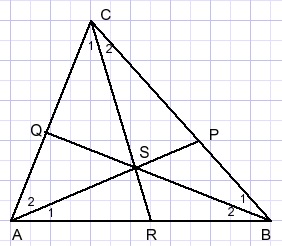
Deze luidt:
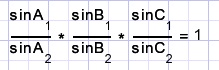
als de lijnen door de hoekpunten door één punt (S) gaan.
Bewijs
Is mogeljk door toepassing van de sinusregel in driehoeken ABS, BCS en ASC.
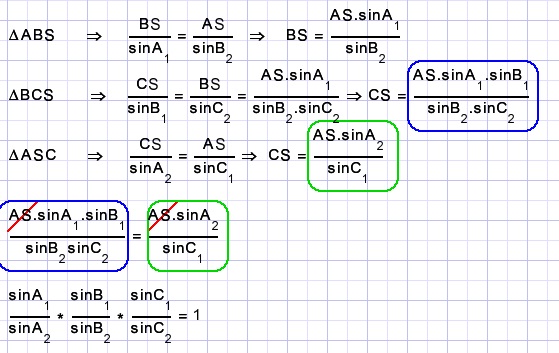
Omgekeerd
Als bovenstaand product van de sinusverhoudingen = 1 dan gaan de lijnen door A,B,C door één punt.

