| Een mechanica probleem |  |
Inleiding
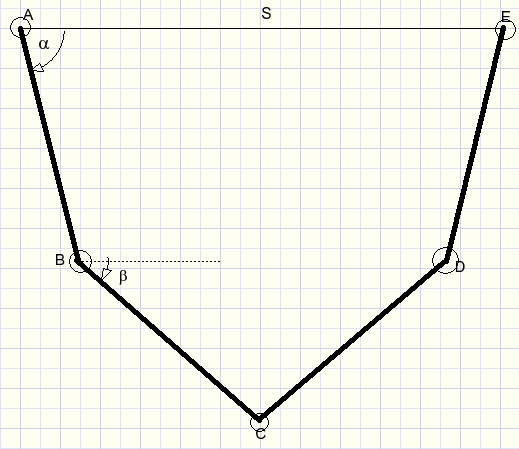
In het plaatje hierboven zijn vier gelijke staven aan elkaar bevestigd.
A,B,C,D,E zijn scharnierende punten.
AE ligt horizontaal.
A en E zijn bevestigingspunten en de afstand S ligt vast.
Vraag:
Als de afstand S en de lengte van de staven bekend zijn hoe groot zijn dan hoeken a, b en afstand BD?
Eerst even wat basiskennis mechanica.
Krachten tekenen
Krachten tekenen we als een gericht lijnstuk, de lengte daarvan is evenredig met de grootte van de kracht.
De kracht werkt in de richting van het pijltje.
Krachten optellen
Twee krachten tellen we op door ze op een parallellogram te tekenen.
De som is dan de diagonaal:
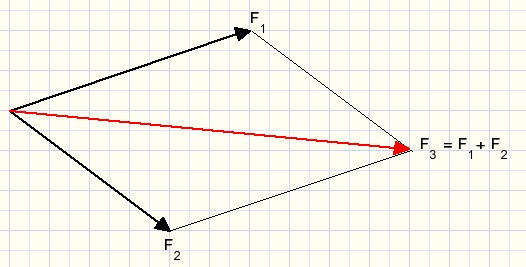
In het plaatje hierboven kunnen krachten F1 en F2 vervangen worden door F3.
Of omgekeerd: kracht F3 kan ontbonden worden in F1 en F2.
Koppel
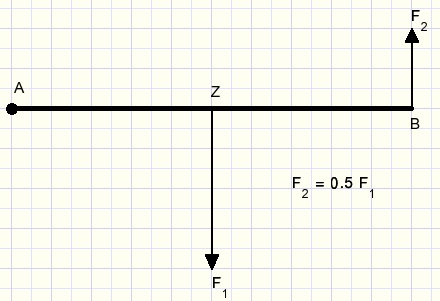
In het volgende plaatje kan staaf AB draaien om punt A.
F1 is het gevolg van de zwaartekracht, die aangrijpt in zwaartepunt Z.
Om de staaf in deze horizontale positie te houden kunnen we in punt Z een kracht tegengesteld aan F1 uitoefenen.
Maar in punt B kunnen we toe met de helft van deze kracht: F2 = 0,5.F1.
Het product kracht x afstand tot (bevestigings)punt heet het koppel.
Evenwicht ontstaat als de som van de koppels nul is.
Hier: F1 . ZA + F2 . BA = 0
Opmerking: als F1 positief is dan is F2 negatief wegens tegengestelde richting.
De reden van deze regel is het behoud van energie = kracht x afstand.
Voor een bepaalde draaiing legt punt B de dubbele weg af van punt Z.
De grote kracht die met tangen en breekijzers kan worden uitgeoefend berust op dit principe.
Overwegingen
Kijk nog eens naar het plaatje bovenaan deze pagina.In het geval van evenwicht heffen alle krachten elkaar op, hun som is nul.
A en E zijn vaste punten.
Krachten uitgeoefend in staven AB en DE worden dus intern gecompenseerd in de bevestigingspunten.
(tenzij de krachten te groot worden en A en E lossscheuren)
Een horizontale kracht in punt C als gevolg van de zwaartekract op staven AB en BC
worden tegengewerkt door even grote krachten van CD en DE.
(het gevolg van de symmetrie)
Een kracht in BC omlaag strekt LABC richting 180 graden.
Een kracht in CB omhoog maakt LABC scherper.
De berekeningen
Alle krachten zijn het gevolg van de zwaartekracht.We stellen deze kracht op 1 per staaf.(onbekende eenheid)
Het volgende plaatje toont de zwaartekracht op staaf AB in zijn zwaartepunt.
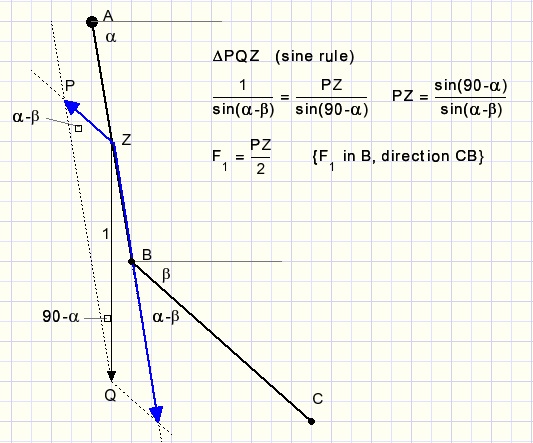
De kracht ZP wordt in punt P door de staaf uitgeoefend door zwaartekracht ZQ=1.
In punt B en richting ZP wordt dus de halve kracht uitgeoefend wegens gelijk koppel.
Deze kracht noemen we F1.
Nu bekijken we de zwaartekracht op staaf BC.
Die hangt aan B en C en daarom werkt in elk punt een kracht 0,5 omlaag.
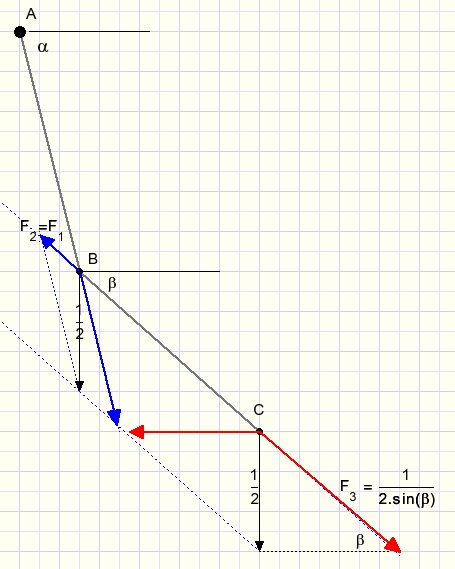
In punt B ontbinden we die kracht in een kracht binnen AB en een kracht F2 = F1 in richting BC.
Dat is eenzelfde berekening als hiervoor.
Kijk nu naar punt C waar de zwaartekract 0,5 is gesplitst in F3 richting BC
en een horizontale kracht.
Die laatste wordt gecompenseerd door de symmetrie van de opstelling.
Evenwicht zal ontstaan als de som van alle krachten in punt B gelijk is aan nul.
Dit is het geval als:
-
F1 + F2 = F3
of
2.F1 = F3
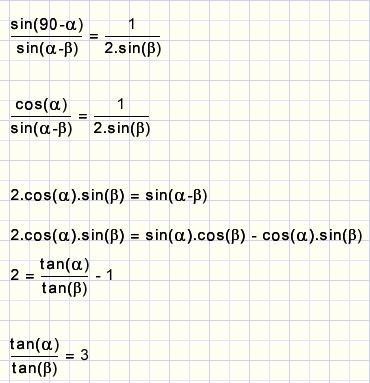
Dit schijnt de voorwaarde te zijn voor evenwicht.
Tijd voor onderzoek.

Vier latten van elk 96cm. lang zijn verbonden waarbij afstand AE wordt gevarieerd.
Steeds is afstand BD opgemeten, waaruit tan(a) en tan(b) werden berekend.
En ziet !
| AE | BD | tan(a) | tan(b) | |
|---|---|---|---|---|
| 50 | 37.5 | 15.327 | 5.02 | 2.95 |
| 75 | 56 | 10.0557 | 3.279 | 3.07 |
| 100 | 74 | 7.3166 | 2.394 | 3.06 |
| 125 | 91 | 5.5578 | 1.858 | 2.99 |
| 150 | 108 | 4.4607 | 1.469 | 3.04 |
| 175 | 124 | 3.6295 | 1.182 | 3.07 |
| 200 | 138 | 2.93087 | 0.9673 | 3.04 |
| 225 | 150.5 | 2.3753 | 0.792 | 3.00 |
Laatste vraag
Als een staaf lengte L heeft en afstand AE = xdat is het probleem de oplossing van deze vergelijkingen:
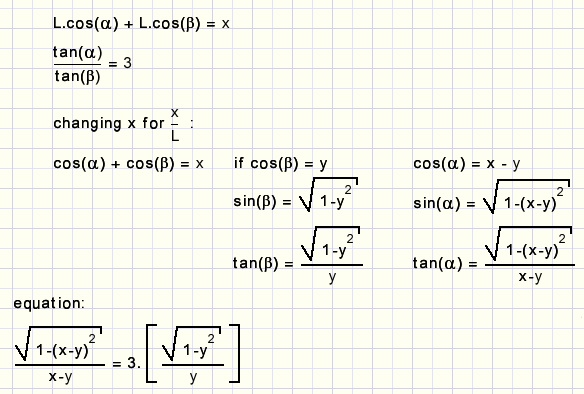
Is het mogelijk deze vergelijking als functie te schrijven dus y = ....x......?
Ik denk het niet.
Dan maar een grafiekje:
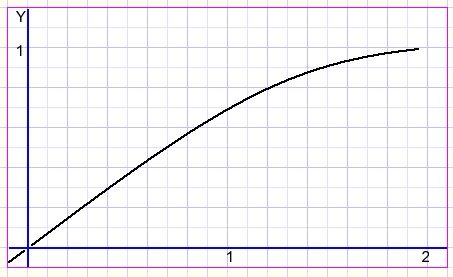
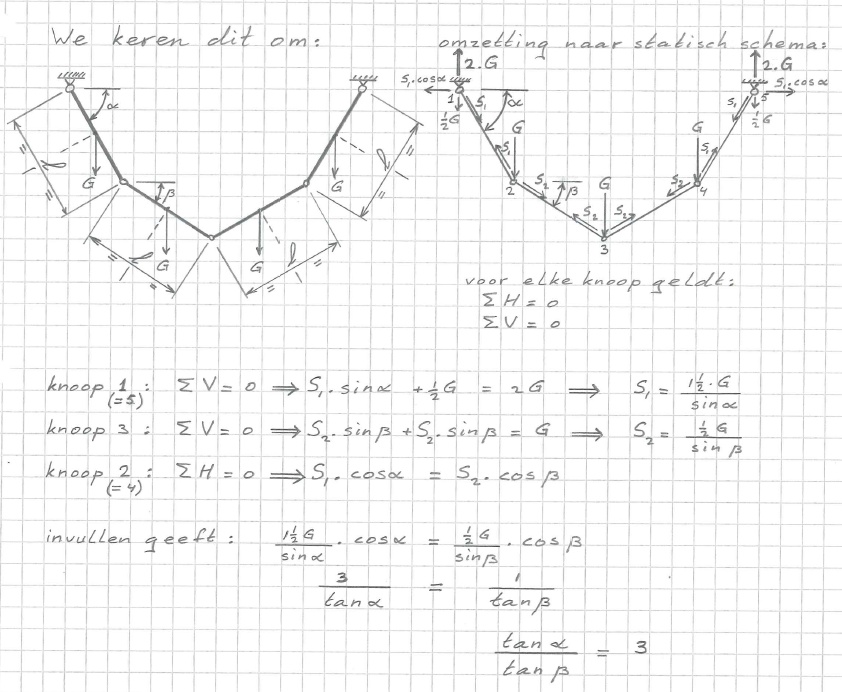
Jan Overduin (constructeur civiele techniek) stuurde de volgende fraaie toepassing.
Bij omdraaiing ontstaat een bekende dakconstructie.

En de berekeningen: