the direction of a vector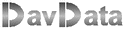

Introduction
In geometry, a vector is a line from one point to another in a plane.
This article describes how to obtain the direction (in degrees) of a vector.
see figure 1 below
Directions are
    0right
    90down
    180left
    270up
all measured in degrees.

We notice vector AB = (a,b) and the tangent equals tan(x) = b/a

Note: positive y direction is down for coordinates on the screen.

Our objective is to calculate x for any vector.

Tangent
The tan function supplies the b/a ratio for a given value of angle x............tan(x) = b/a
The inverse tangent function arctan supplies the angle x for a given value of b/a........x = arctan(b/a)
However, x is in radians.
Knowing that 2*p radians = 360 degrees, we simply multiply by 180/p to convert radians to degrees.

Figure 2 shows the arctan function.
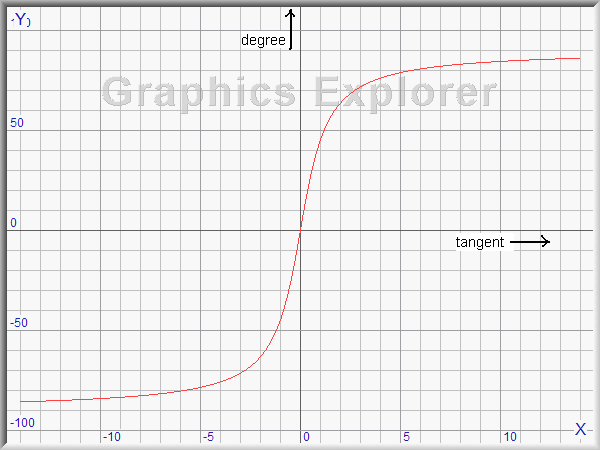
We actually plot (Graphics-Explorer) the equation y = atan(x) where x is ratio b/a and degrees
are selected instead of radians.

The atan function result ranges from -90......+90 degrees, which is not what we want.
Also, for straight up or down vectors where a = 0 , an exception (error) is generated because of
division by zero ......{ atan(b/0) }

So, we need some extra lines of code to obtain the correct results.

The function "Angle"
function Angle(x1,y1,x2,y2) calculates the direction of a line from (x1,y1) ---> (x2,y2).

The first step is to test for vertical lines (x1 = x2).
In this case the result is 0.5*p (90 degrees) or 1.5*p (270 degrees).

In case x2 < x1 , p is added which fixes all angles from 0..270 degrees.
However, angles from 270 to 360 degrees are still shown as -90 to 0 degrees.
This is fixed by adding 2*p (360 degrees) in case of a negative result.

The program
function Angle(x1,y1,x2,y2 : integer) : single;
//return angle of line
//right  = 0; down = pi/2 (90) ; left = pi (180) ; up = 3pi/2 (270)
begin
 if x1 = x2 then
  begin
   if y2 > y1 then result := 0.5*pi else result := 1.5*pi;
   exit;
  end;
 result := arctan((y2-y1)/(x2-x1));
 if x2 < x1 then result := result + pi;
 if result < 0 then result := result + 2*pi;
 result := result * 180 / pi;  //make degrees
end;

Click at right top of this page to download the program.
Select "show angles" , move mouse pointer over screen, press mousebutton and hold while moving mouse.