Solving Tectonic puzzles

Tectonic, also called Suguru, is a number puzzle.
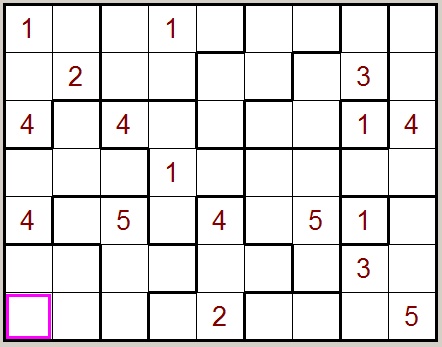
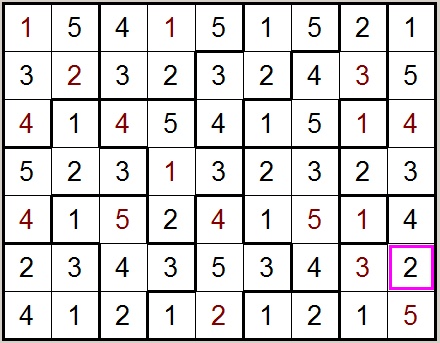
Below is pictured such a puzzle: left is the initial state, right shows the solved state.


This is a 9x7 (columns x rows) puzzle.

Rules

We notice 9x7 cells which are grouped in blocks of 1 to 5 cells.
The boundaries of a block are painted in heavy lines.
Each block of n cells must contain the digits 1,..,n just once.
So, a block of only one cell must have number 1.
A block of 2 cells contains cells with numbers 1,2.
A block with three cells: 1,2,3...etc.

The second rule is that adjacent cells may not have the same number.
Adjacent means horizontal, vertical or diagonal.
If a cell contains number 1 all neighbour cells
    - 3 around a corner
    - 5 around an edge
    - 8 other
cannot hold "1".

In the original puzzle some numbers are filled in already.
These numbers are colored brown by my tectonic helper program.
Solving a tectonic puzzle is finding the numbers of the empty cells.
This is done by analytic reasoning.

The next part of this article describes tectonic solving techniques.
I do not pretend completeness.
The rules presented are the result of my own experience.
Feel free to comment.

Options

The options of a cell are all the numbers that fit at a certain time.
In an initial puzzle most cells will show many options.
Solving a puzzle is eliminating options until each cell has one single option left.

Single option cells

These are cells where only one number fits.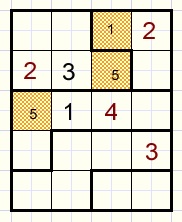



In the colored cells only one option is possible.

Single cell in block that has option

A cell may be the only one in a block that holds a certain option.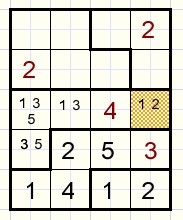



The marked cell is the only one in it's block that holds option "2".
So number 2 must be written in this cell.

Connections

All cells in a block have different numbers, so they "see" each other.
We say that these cells are "connected".
Any cell also "sees" it's surrounding neighbour cells (3, 5 or 8 depending on it's position).
So, this cell is "connected" to it's neighbours.
Connected cells must have different numbers.

Groups

Definition:
n cells form a group if
    - they are all connected to each other
    - together they have n options
For the options in a group any combination from 1..5 is fine.
Groups may reside inside a block or cover more than one block.
Groups may overlap each other and are dynamic, they change when a number is written in a cell.
Any combination of cells in a solved block form a group.
While analyses progresses and options are reduced, the number of groups increases.

Option reduction in blocks

Here we see groups within a block.
A group (of cells) eventually have all their options filled in.
So, a cell that connects to all cells of the group cannot have any of the group options.
The options that must be removed are painted red.



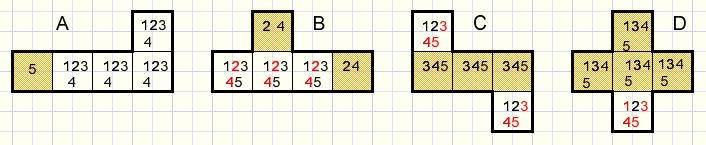
We see a block of 5 cells, pictured four times.
Groups within the block are painted with a colored background.

A.
Group of 1.
One cell has "5" as the only option.
The other cells of the block cannot have option 5.

B.
Group of 2.
A group has (2,4) as options.
So the "2" and "4" options in the other cells of the block must be removed.

C.
A group of 3 with options (3,4,5).
These options must be removed in the other cells.

D.
A group of 4 with options (1,3,4,5).
These options must be removed in the other cell of the block.
Note: this is the "single cell for option" case mentioned before.

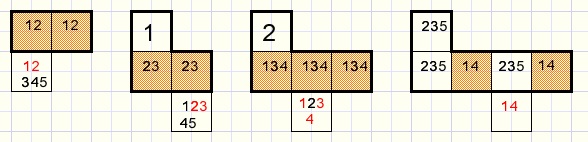
Cell/Block interaction

If a cell outside a block connects to all cells of a group within that block then
this cell cannot have any option of that group.
See picture below where the red options must be removed.



Interlude

The hint reduction methods described before are already implemented in my tectonic-helper program.
Pressing the HINT button shows options that may be eliminated.
All puzzles could be solved by these hints so far.
Until recently when I received several puzzles where my helper did not find hints
for puzzles that were far from solved.
I realized that I had overlooked one important property of tectonic puzzles:
opposite Sudoku, cells of a tectonic puzzle affect each other crossing the boundary of their block.
For that reason I introduced the term "group".
The next part of this article is an attempt to use the properties of groups for option reduction.
My planning is to implement these new rules in version 3 of the tectonic helper.
Again: feel free to comment.

Groups covering different blocks

Groups of 2 cells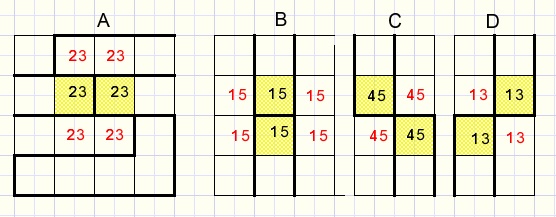



The black numbers are the group options in different blocks.
The red options cannot exist and have to be removed.

Below is a more abstract (graph) notation which applies to Sudoku as well and tectonic:



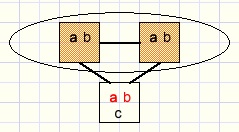
groups of 3 cells



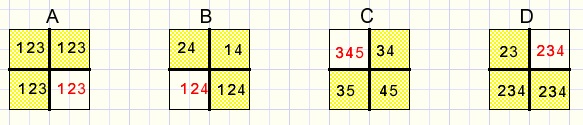
We see group A with options (1,2,3), B(1,2,4), C(3,4,5) and D(3,3,4).
In real puzzles these groups are harder to recognize.
Abstract graph notation:



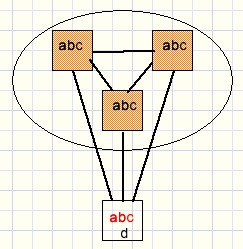
Summary

As we realize now, all option reduction methods so far may be summarized by one single rule:
    - a cell that connects to all cells of a group cannot have any option of that group.
However, this rule must be refined.

Cells partially connected to a group

Definition:
A cell is partially connected to a group if it connects to some but not all cells of the group.

So, in the group we see "connected" and "disconnected" cells.
Rule:
    if a cell partially connects to a group
    it cannot have group options that are absent in the disconnected cells.



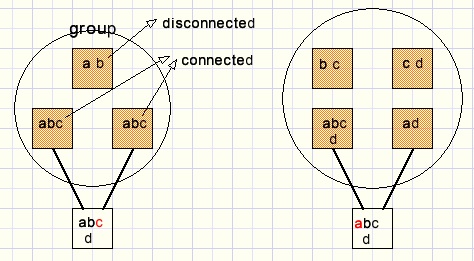
This is obvious because these options have to show up in the connected cells.
The red colored options in the cells must be removed.
Also, this rule does not contradicts previous ones:
if a cell connects to all cells of a group the (virtual) disconnected cells have no options.

Example (1)



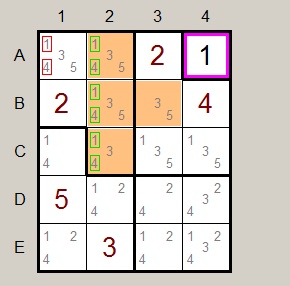
A2,B2,C2,B3 form a group.
A1 partially connects to this group.
A1 cannot have options (1,4) because such a number would delete the options in the group.

Example (2)



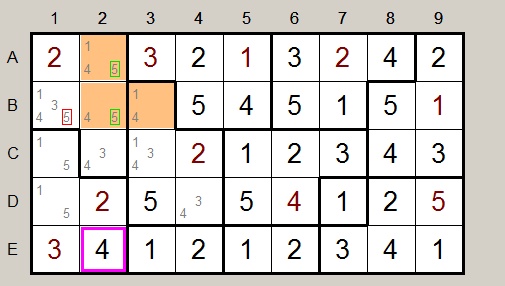
B1 partially connects to group A2,B2,B3.
B1 cannot be 5 because his would kill option 5 in the group.

Example (3)



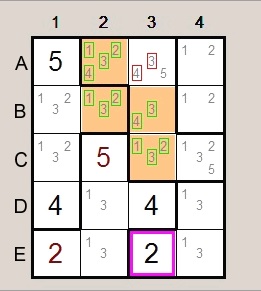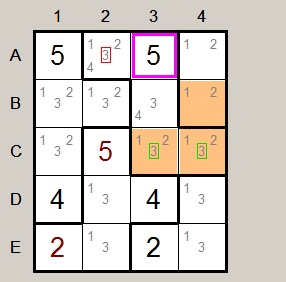Left picture:
See group A2,B2,B3,C3.
A3 connects to all cells of group so A3 cannot have options (3,4).

Right picture:
See group B4,C3,C4.
A2 partially connects to group so cannot have option 3.

Flip-Flops

This is not an option removing method, but a help in the analysis.
If groups of 2 options are overlapping, possible numbers of their cells alternate.



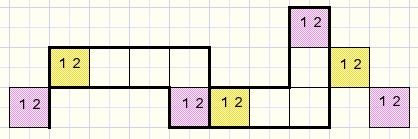
Equal colored cells eventually recieve the same number.

Equality




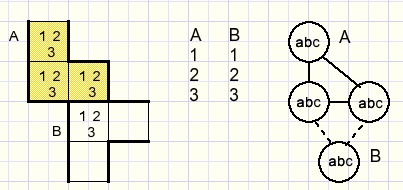
Fields A and B must hold the same number.

Connected groups

2 groups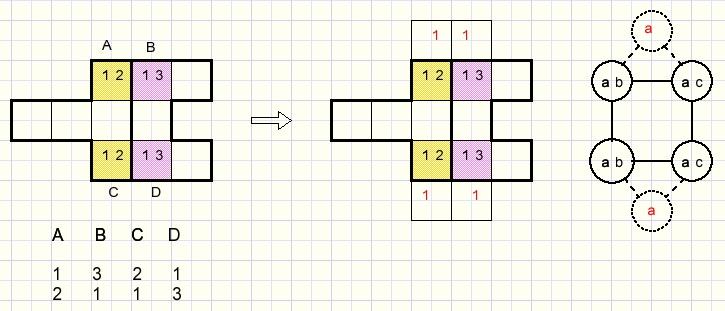



In either case cell A or cell B equals 1.
The same is true for cells C and D.
So, a cell that connects to A and B or connects to C and D, cannot have option "1".

Example:



The colored (1,3) cells are equal.
The other (1,2) colored cells are unequal.
Equal cells connect to unequal cells for option (1),
so option (1) must be cancelled in the purple (1,3) cells.
After that the puzzle solves easily.

I am sure more rules remain to be discovered.
There are several ways to look at a puzzle.
Interesting thought is that, as analysis progresses, the number of groups increases.
In a solved puzzle all interconnecting 2, 3 or 4 cells form a group.

If analysis fails however we arrive at the last resort.

Backtracking

Backtracking is a sytematical "trial and error" approach.
This is the procedure:
    1. save the game
    2. write a number in some cell (cell and number are remembered).
    3. try to solve the puzzle, if no hints: goto 1.
    4. if error (field without options)
      5. reload. If no reload possible: exit, no solution
      6. try next number in cell
      7. if all options tried: goto 5.
      8. goto 3.
Backtracking will be implemented in the next version 3 of the tectonic helper.