A perfect squares problem

download program

download Delphi project

I wondered if there would exist perfect squares of 10 digits long that count every digit 0..9 just once.
The lowest number could be 0123456789 which is the (not perfect) square of 11111.xxxxx
The highest number could be 9876543210 which is the (not perfect) square of 99380.xxxx

There are two approaches to solve this problem:
1.
generate all permutations of elements 0..9 which are 10!=3628800 cases.
Calculate the roots and check for an integer value.
2.
Count from 11111 to 99380, square each number and check for digits 0..9.
Method 2 is used here.

My Delphi version is 32 bit, so 9876543210 slightly exceeds the 32 bit (longword) range
which is 0..4294967295.
This may be overcome by splitting the numbers over 16 bit words.
By defining 4 decimal digits per word we actually calculate with a base of 10000 (0000..9999).
This method (2A) is described first.

Delphi-7 supports limited 64 bit integer (Int64) operations including the inttostr function.
This method (2B) is described next.

Method 2A
num is the number to investigate.
Initial value of num is 11111.

1 - square num, the product is num2.
2 - test num2 for digits 0..9 each occurring once.
3 - if test is OK, display num and num2 in a Tmemo component.
4 - increment num.
repeat steps 1..4 until num reaches 99380

Data formats

var num   : array[0..1] of word;
    num2  : array[0..2] of cardinal;//square of num
    snum2 : string;                 //string of num2

num: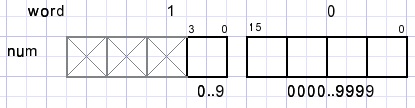

num2:

Procedures

procedure incNum;
//increment num
begin
 inc(num[0]);
 if num[0] = 10000 then begin
                          num[0] := 0;
                          inc(num[1]);
                        end;
end;

procedure squareNum;
//make num2
var i,j : byte;
begin
 for i := 0 to 2 do num2[i] := 0; //clear
 for i := 0 to 1 do
  for j := 0 to 1 do
   begin
    num2[i+j] := num2[i+j] + num[i]*num[j];
   end;
 for i := 0 to 2 do
  if num2[i] > 10000 then
   begin
    num2[i+1] := num2[i+1] + (num2[i] div 10000);
    num2[i] := num2[i] mod 10000;
   end;
end;

function test : boolean;
//test num2 for digits 0..9
var dbits,w: word;
    d,i : byte;
begin
 w := 0;
 dbits := 0;
 snum2 := '';
 for i := 0 to 9 do
  begin
   case i of
    0 : w := num2[0];
    4 : w := num2[1];
    8 : w := num2[2];
   end;
   d := w mod 10;
   w := w div 10;
   dbits := dbits or (1 shl d);
   insert(chr(ord('0')+d),snum2,1);
  end;//for
 result := dbits = $3ff;
end;

procedure TForm1.Button1Click(Sender: TObject);
//GO (2A)
begin
 memo1.Clear;
 num[0] := 1111;
 num[1] := 1;
 repeat
  squareNum;
  if test then report;
  incNum;
 until (num[1] = 9) and (num[0] > 9380);
 label1.Caption := 'squares found: '+inttostr(memo1.Lines.count);
end;

Unique digit test
Extract 10 digits from num2.
Set bit d in word dbit for digit d.
After a succesfull test dbits must be $3ff.

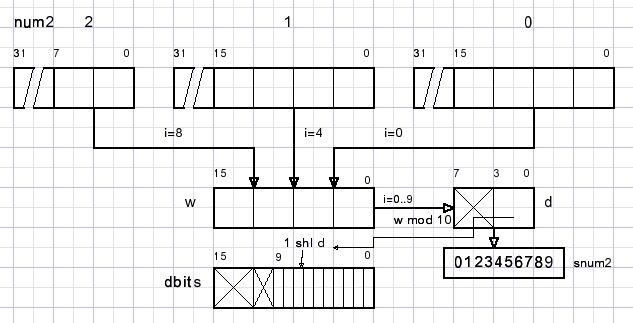
Method 2B
Using the Int64 data format.

procedure TForm1.Button2Click(Sender: TObject);
//GO-2B
var t1,t2,n,n2 : Int64;
    w : word;
    s,sn : string;
    d,i : byte;
    pt : double;
begin
 memo1.Clear;
 n :=11111;
 t1 := GetCPUticks;
 repeat
  n2 := n*n;
  sn := inttostr(n2);
  if length(sn) = 9 then insert('0',sn,1);
  w := 0;
  for i := 1 to 10 do
   begin
    d := byte(sn[i])-ord('0');
    w := w or (1 shl d);
   end;
  if w = $3ff then memo1.Lines.Add(inttostr(n)+'  '+sn);
  inc(n);
 until n > 99380;
 t2 := GetCPUticks;
 s := 'squares found: '+inttostr(memo1.Lines.count);
 pt := 0.001*proctime(t2-t1);
 s := s + '; time= '+formatfloat('###0.000',pt)+ ' msecs';
 label1.Caption := s;
end;

Processing times.
Suppressing the memo1.lines.add( ) statements compares true calculation times.
Method 2B appears to be 10 times faster than method2A.

CPU clock
Function GetCPUticks returns the number of CPU clock cycles since power on.
Procedure setCPUclock sets variable clockrate during startup.
Function proctime returns the elapsed time in microseconds.
See the timer unit.

This concludes the program description.