how to paint spirals

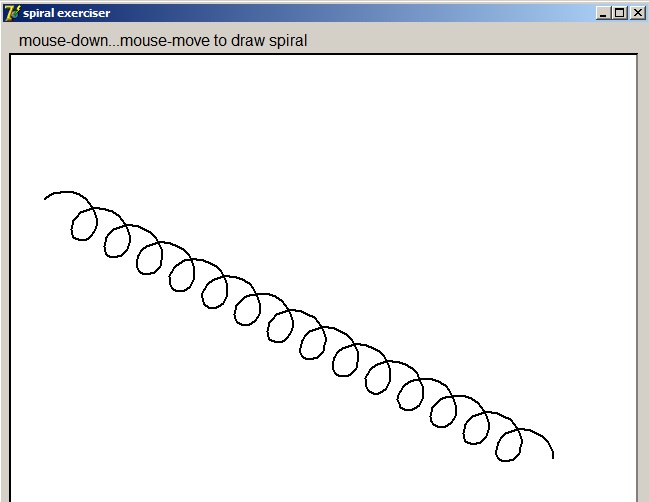
Painting Spirals

load program

load complete Delphi-7 project

This article explains how to paint spirals in the Delphi programming language.
Also your high-school math is refreshed.

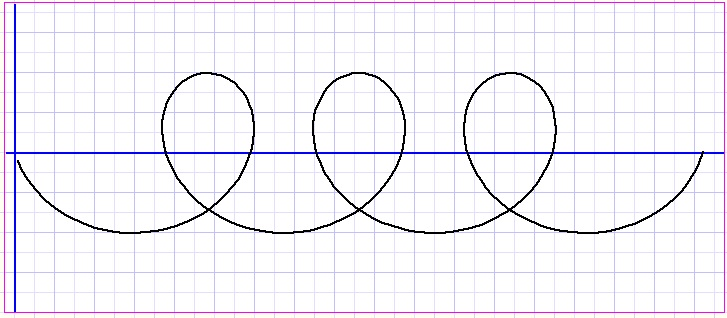
A spiral paint is the addition of two pen movements:

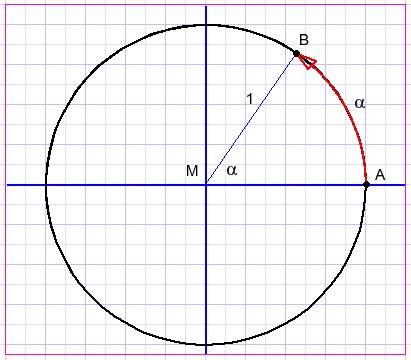
Measuring angles in radians

Consider a circle with a radius of 1.
We measure the angle a at center M by the length of the arc AB.
Since the perimeter of a circle having a radius of 1 equals 2*pi,
2*pi radians is the angle representing a full circle (360 degrees).
So, an angle of size a spans an arc of length a (if the radius = 1)
Of course, if the radius = r, angle a spans an arc of length ar

Painting a circle

A circle may be painted by moving a point P at equal distance r around center M
interconnecting points P by straight lines.

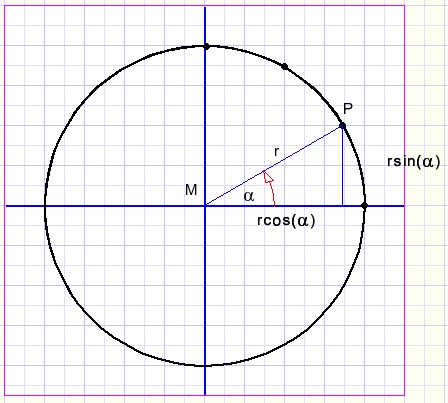
The angle a is incremented in small steps and for each step the coordinates of P are calculated:

The spiral starts at (x1,y1) and ends in (x2,y2).
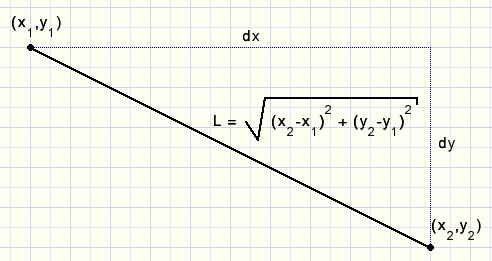
So, the length L of the straight line between these points is sqrt(sqr(x2-x1)+sqr(y2-y1)).
(sqrt is square root, sqr is square).
Now, referring to the image at the top, we notice that the spiral must have a count
of 3, 5, 7, 9..... half turns, depending on the length L.

Next question is: "how many half turns do we need"?
This number is obtained by dividing L by radius r (but other values than r may be choosen).
Now, the L/r quotient has to be rounded to 3, 5, 7 so...to an odd number.

Rounding values to odd integers (1,3,5....)

When confronted with a new problem, a good way to start is regression to a similar problem
which has been solved.
We know how to round a number to the nearest positive integer:
add 0.5 and truncate (remove digits right of decimal point).
Rounding a number to a multiple of 2: add 1, divide by 2, truncate and multiply by 2.
Now rounding to an odd number:
Subtract 1 to make number even, round to multiple of 2, finally add one to make the number odd.
We notice that the subtract 1 and add 1 operations cancel each other so what remains:
Divide number by 2, truncate, multiply by 2, add 1.

Painting the spiral

On a computer canvas, the y coordinate increases when going down.
Increasing an angle causes clockwise motion.
In the figure below a spiral is painted starting at point A(x1,y1) and ending in B(x2,y2).
During this process, the circle center moves from M1 to M2.
M1-M2 = L - 2r.

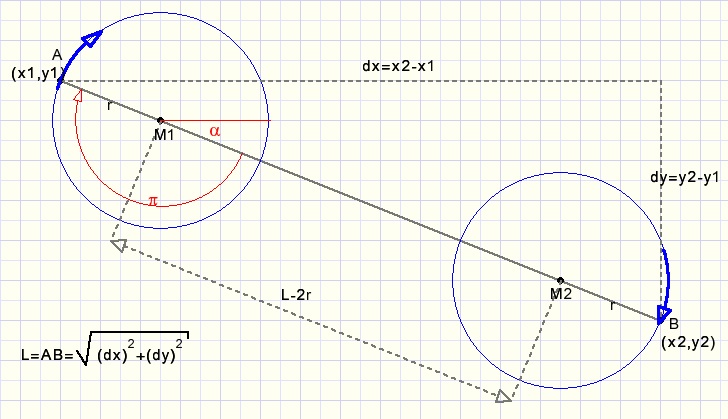
The first step is to calculate dx = x2-x1.
Next calculate dy = y2 - y1.
Next: L = sqrt(sqr(dx) + sqr(dy)).
Next: calculate L/r and round this value to the nearest odd number, call this number n.

The variable that controls the painting is phi, the angle in radians.
phi runs from 0 to maxphi=n*pi, the number of half circles.

In the picture above we notice however, that phi has to start at value a + p
this value is called phibias = arctan(dy/dx) + pi.
Painting a half circle in 12 steps needs a phi increment of pi12 = pi/12 per step.
dL is the increment by which circle center M is moved along AB at each step.
dL = (L-2r)/maxphi.

At start, the pen is moved to (x1,y1).
pL is the distance AM: pL = r + phi*dL.
dxL = dx/L
dyL = dy/L
circle y coordinate: a = r*sin(phi+phibias)
circle x coordinate: b = r*cos(phi+phibias)
(sx,sy) are point M coordinates on line AB:
sy = y1 + dyL*pL
sx = x1 + dxL*pL
pen destination : lineto(sx+b,sy+a)
update ...phi := phi + pi12

phi is incremented until maxphi is exceeded.
In the above calculations, rounding to integers is not shown.
Please refer to the source code.

A last concern is the relative position of points A and B.
The only value however that needs special considerations here is phibias
where pi is not added if x1 > x2.
Also x1 = x2 needs some extra lines of code to avoid a floating point exception.

The project

The project consists of a single form with paintbox and a unit.
Mouse down, -move and -up events control a simple drawing mechanism.
Radius r is fixed at 20.
The painting is done by procedure paintcoil(x1,y1,x2,y2,r: smallint):

procedure paintcoil(x1,y1,x2,y2,r: smallint);
var phi,pi12,maxphi,phibias,dL,dx,dy,dxL,dyL : single;
    a,b,n,L,pL,sx,sy: smallInt;
begin
 pi12 := pi/12;
 dx := x2-x1;
 dy := y2-y1;
 if dx > 0 then phibias := pi + arctan(dy/dx)
  else if dx < 0 then phibias := arctan(dy/dx)
        else if y2 > y1 then phibias := -pi/2 else phibias := pi/2;
 L := round(sqrt(sqr(dx)+sqr(dy)));
 n := trunc(L/(2*r))*2+1;
 maxphi := n*pi;
 dL := (L-2*r)/maxphi;
 dxL := dx/L;
 dyL := dy/L;
 with form1.paintbox1.canvas do
  begin
   pen.width := 2;
   pen.color := $000000;
   moveto(x1,y1);
   phi := pi12;
   while phi <= maxphi do
    begin
     pL := r + round(phi*dL);
     a := round(r*sin(phi+phibias));
     b := round(r*cos(phi+phibias));
     sy := y1 + round(dyL*pL);
     sx := x1 + round(dxL*pL);
     lineto(sx+b,sy+a);
     phi := phi + pi12;
    end;
  end;//with
end;

Below a picture of the program at work: