download
spic		 An algorithm for image compression
download complete Delphi-7 project

New SPIC version

New version 5 offers
    - loading of .bmp and .jpg images
    - storing of .bmp and .pic images
    - images size up to 4000 * 3000 pixels (h*v)
download spic5 program download complete Delphi-7 project

Image Compression

This article describes my Delphi project spic for the compression of pictures.
The images are stored in bitmaps.
From the pixels of this bitmap, spic generates a file of type .pic
which is much smaller in byte count then the .bmp file holding the original bitmap.

Well known formats for compressed images are : .gif , .jpg and .png.
Later in this article I include a comparison of them with the .pic format.

In general, two type of images may be distinguished: photographs and geometric figures.
The first category has fluent colors and no sharp boundaries,
the second have lines and rectangles filled with a single color.

My spic project is aimed at photographs and paintings.
For geometric pictures other approaches would yield better results however, the .pic files are far from bad.

Below is a reduced picture of spic at work:
The naval battle painting was reduced to 16,07%.

The algorithm

A bitmap with randomly colored pixels will be hard to compress.
Compression is possible only if the picture has some regularity: repeating patterns, areas with less colors.
I tested a lot of methods and so, in an organic way, the algorithm evolved
that works best for picures like the naval battle.
Surprisingly enough, only a limited number of simple commands remained.

Colors.

A bitmap in true color format has 24 bit colors, which are stored in the pf32 bit format as pictured below:
The intensity of the red, green and blue primary colors ranges 00000000 .. 11111111 (0..255) so, 8 bits per color.
Spic uses this 32 bit pixelformat because addressing the pixels is very fast and simple.

For the human eye, the difference between colors varying only in the lower bits is not visible.
Some experimenting revealed that realistic colors remain even if a color is rounded to multiples of 16.
Sixteen choices for red, green and blue make 12 bit colors ranging from 0 to 4095.
This looks like a dramatic loss but how big is the "error" caused by this rounding?
Rounding 1110 1000 to 1111 0000 is an "error" of 8/256 = 3,125%.
Actually a little more because differences in the higher colors are more visible then in the lower color values.
Another, however small, reduction is to replace the color 0000 0000 by 0001 0000., so eliminating color 0.
The difference between 0000 0000 and 0001 0000 is not visible.
So, the red, green and blue primary colors have 15 intensities: 0001 .. 1111 binary.

The naval battle painting is shown in this format and I see no difference with the original 24 bit pixel image.

Rounding is done in a somewhat different way as expected.
In general, rounding of a number to a multiple is done by
    - adding half the value of the multiple to the number
    - chop off the number at the multiple.
The following problem shows up when rounding 1111 1100 to a multiple of 16:
    1111 1100
    0000 1000 + 8
    ----------------
    10000 0100 chop the lower 4 bits (= multiple of 16)
    10000 0000
The new color value is 16, which exceeds the 4 bit space.
To avoid this situation, -1- is subtracted so, 1 0000 - 1 = 1111 .
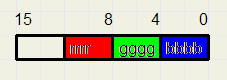
The final result is that primary colors are reduced to 12 bits,
hexadecimally $1 .. $f where $1 stands for true color $1f and $f stands for $ff.
The minimum 12 bit true color is $111, the maximal color (white) is $fff.
Rounding $ff to $f0 would have caused loss of brightness.

Pixels

When coloring a bitmap there are two variables: the position coordinates and the color itself.
In our case, the color needs 12 bits, but the position needs about 2 * 10 = 20 bits.
So, it is more convenient to addres the pixels in a sequential way and selecting the color then the opposite.
When scanning the pixels sequentially, spic has five ways to select the color:
    1. copying the color from the left (previous) neighbour pixel
    2. copying the color from the top neighbour
    3. selecting the color from recently used colors, saved in a stack
    4. apply a small change to the left neighbour color
    5. adding a new color
In early programs, the scanning was horizontally, line by line, from the left top to the right bottom.
Later scanning was done like illustrated below: in 4 x 4 pixel blocks from left top to right bottom.
This yields more reduction.
In later versions of spic I enlarged the blocksize to 16* 16 for more compression.
Each pixel is addressed once to select it's color.
The 5 command codes are 2 bits in length, in some cases a subcommand and extra bits are necessary
for the stack address or a new color.
    00 00 rrrr gggg bbbb new color: red, green,blue
    00 01 Hmarker
    00 10 Vmarker
    00 11 rgb ddd Delta
    01 ssssscolor from stack[sssss] (0..31)
    10 copy color from left neighbour
    11 copy color from top neighbour
In the most unfavourable case where for each pixel a new color is required,
the reduction is 16/24 = 66,7% relative to the 24bit pixelformat.

In the case where all pixels copy the color of a neighbour (most favourable) the reduction is 2/24=8,3% .
Much more, as we will see.

Selecting a color from the stack yields a reduction to 7/24 = 29%.

I varied quite a lot with the command codes.
Short codes for cases that occur most frequent, longer codes for complicated operations as coloring an area at once.
You could use a single -1- for a command and for the next command -01- the next -001-
many variations are possible. But to my surprise, the method above performed best.

Markers

A .pic file is a bitstream of commands that describe the image in a predefined sequence.
If sequential pixels all copy their color from the left neighbour, which occurs frequently, the bitstream looks like:
    1010101010101010....
Geometric pictures produce this pattern many times.
This makes one look for a method to compress this bitstream as well.
An approach would be to "pack" the bitstream in an envelope of new commands,
but these extra bits lower the reduction percentage.
Would there be a method that does not have this disadvantage?
In the early version of spic an unused code combination "housed" this extra compression code.
But bitstream compression yielded so much reduction, that it proved more benificial
to enlarge some other codes to allow short codes for the compression of both -10101010- and -11111111- streams.

Markers stand for a bitstream. The Hmarker for -10101010- and the VMarker for -11111111- .
At once, the reduction is 50% as the marker is 4 bits in size.
So, in the compression proces, -10- and -11- codes are stored until four of them are replaced by their marker.
But there is more. After a marker is written, the program is in marked mode.
An additional four -10- or -11- codes are now replaced by a single -1- until another code is scanned
and the marked mode is ended by writing a single -0- to the director.
For 12 sequential -10- or -11- codes, the total reduction is (4+1+1+1)/(12*24) = 2,4%

The stack

A stack length of 32 colors performed best.
For each scanned pixel, the color is presented to the stack.
If the color is allready in the stack, say at position n, then colors 0..n-1 are shifted one place down
and color n is placed at the top of the stack.
A new color is placed at the top of the stack pushing colors 0..30 down, overwriting color 31.
The stack always contains the most recent 32 colors.

Delta

Paintings and photographs have fluent colors.
Many times, there is only a small difference between neighbouring colors.
The delta command slightly modifies the left neighbour.

The rgb field is 3 bits in length, 1 bit for each primary color. It's meaning is:
    0 : no change for this primary color
    1 : change, selected by the corresponding d bit
The ddd field also has 1 bit per primary color:
    0 : +1 but: if color $f then -2
    1 : -1 but: if color $1 then +2

Summary

Below, all color selection possibilities for a pixel are summarized: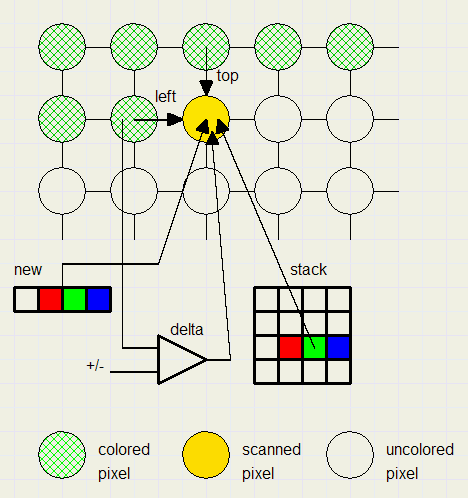

File format

The command codes are written to array[0.. maxdir] of dword named director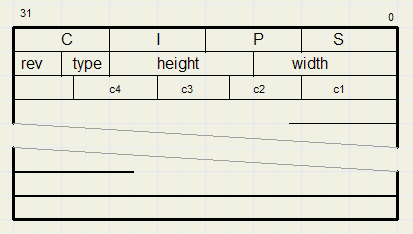
The first dword is file identification, the second holds bitmap dimensions,
file type (4 or 12 for color depth) and a revision number.c1,c2...are the bitstream command codes.

Trics that didn't make it.

1. The Mixer
This command had format xx rgb.
If r=0 the red color was copied from the left neighbour, r=1: the top neighbour etc.
The number of hits were too low to allow the extra code.

2. Friendly colors
In an array[0..7, 0..4095] up to 8 neighbours per color were saved.
Same disadvantage as 1.

3. Multiple pixel commands
I tried this in earlier programs, but reduction never was better than 30% except for geometric figures.

This concludes the description of the compression algorithm of the .pic format.

It may be denoted as"RISC" (reduced instruction set) .
The secret are the short command codes together with bitsream compression.

Greyscale

An option is the conversion of a picture from color to greyscale.
In this case all red, green and blue 4 bit fields have the same value.(1..15)
A different command set applies:
    00 00 delta +
    00 01 Hmarker
    00 10 Vmarker
    00 11 delta -
    01 ggggnew color
    10copy left pixelcolor
    11copy top pixelcolor
Use of the stack is no advantage because a color is only 4 bits in length.

The grey color is calculated by adding r,g,b and division by 3.
    (rrrr 1111 + gggg 1111 + bbbb 1111 ) / 3 or $0f0f0f

Bitmap adressing

Immediately after loading, the bitmap is converted to the 32bit format by
    bm.pixelformat := pf32bit
The layout was described earlier.
The TBitmap class has a property scanline[y] , which delivers the pointer to the first pixel of a row.
I like pointers as dword for easy calculation: 
type PDW = ^dword;
var po,ps,p : dword;
.....
p0 := dword(scanline[0]);
ps := p0-dword(scanline[1];//ps = pointer step between successive     
                           //rows
Pixel [x,y] can be read by 
p := p0 - y*ps + (x shl 2); // x * 4 for byte to dword address                     
color := PDW(p)^;
Note: p + ps points to the top neighbour of p.

Edges

For y = 0 there is no top neighbour, for x=0 there is no left neighbour.
But assume a white frame around the picture.
In this way, commands -10- and -11- may be used to paint a pixel white at the left or top edge.

Bitstreams

.pic files consist of many short bitstrings of different length.
The pic data is stored in an array called director.
Variabele dirPtr is it's index.
To accumulate the bit packages before storage into the director table, a dword called accu is used.
Variable acount holds the number of bits allready in the accu. 
var director : array[0..maxdir] of dword;
      dirPtr : dword;
      accu   : dword;
      acount : byte;
Below is pictured the storage of bitstrings 1,2,3:
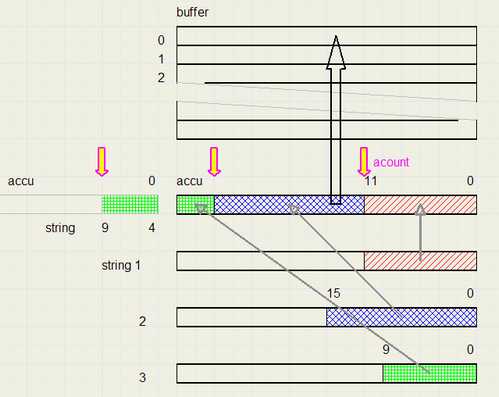
If the accu is full (acount = 32) the accu is stored to director[dirPtr] and dirPtr is increased by 1.
acount is reset to 0.
Above, the accu is painted twice for clarity.
It shows the destination of the piece of bitstring 3 that did not fit the accu.

Reading the director list extracts the lowest bits first. If package 10101010 is written in one command
and the bits are read back one by one, then the right -0- will show up first, followed by the -1- .

Results

Below are listed some results for different pictures (shown miniaturized)
    naval battlehousesMadoffraster stripesfill
    name% gif% png% pic
    naval battle23,666,216,07
    houses18,157,514,75
    Madoff1714,812,39
    raster10,52,54
    stripes0,970,972,06
    fill0,890,4610,81
The text in the "Madoff" cartoon ( Madoff questioned by the police) is:
"Where did you get the idea of paying early investors with the money of late investors?".
Answer: "from the social security system".

png is strong in the case of geometric pictures but weak at photographs and paintings.
jpg (not listed) however is very strong, but at the expense of some quality loss.
The naval battle is reduced to 33% by jpg at 100% quality.
However at 50% quality, the compression is 4,2% , very impressive.
If the dimensions of a picture are reduced by 50% followed by pic compression
then the result would be 0.25 * 16,07 = 4%.
Of course, the picture must be painted two times enlarged in this case.

The spic project

This delphi-7 project consists of
    - form1 / unit1
      - buttons for load, store, compress, decompress, greyscale
      - event methods
      - program control
      - statistics
      - paintbox for display of the bitmaps
      - labels for the display of bitmap dimensions and statistics
    - compressunit
      - procedures for compression / decompression
      - procedures for color counting for statistic purposes

Data flows

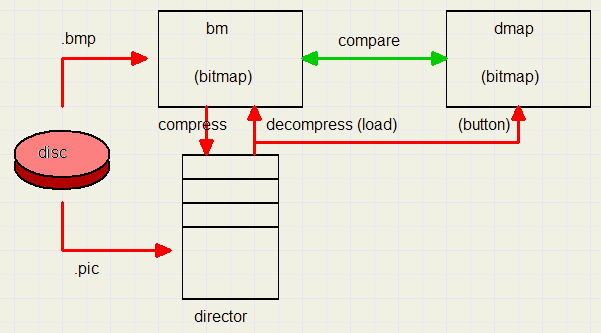
After decompression of the directorlist to a bitmap (dmap) a pixel by pixel comparison takes place
between bitmaps bm and dmap.
It took me a week of debugging to achieve an error free comparison.

Ahh, there is an extra bitmap : backupmap that holds a copy of the original .bmp file.
A click on the restore button reloads bm from backupmap.

Data formats

12 bit colors in a bitmap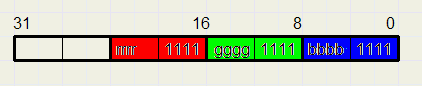
12 bit colors in stack
Counting of the number of different colors is for statistical reasons only. In a 128 dwords table, there are 4096 bits, each corresponding with a possible 12 bits color.
If a color exists, the bit in the table is set to -1- .
All pixels are tested and afterward the -1- bits are counted.

Program code

To conclude this article I show some of the Delpi code.

1. Reading and writing bitstreams from / to the director table
The implementation part of the compressunit starts with 
type PDW = ^dword;

const maxdir   = 250000;
      stacklength = 32;
      pic = 'pic';
      spic = 'spic';
      
var director    : array[0..maxdir] of dword;
    dirPtr      : dword;
    accu        : dword;  //bit asembly register
    acount      : byte;   //nr of valid bitsin accu
    map         : Tbitmap;
    p0          : dword;  //left top canvas pointer
    ps          : dword;  //line downstep value
    cc          : array[0..127] of dword; //colorcount bits
    stack       : array[0..stacklength-1] of word;   //rrrrggggbbbb
writing of n bits to the director: 
procedure storeCode(w : dword; n : byte);
//store n bits of w to dirictor (via accu)
//n = 1 ..16
var space : byte;
begin
 space := 32 - acount;
 accu := accu or (w shl acount);
 if space >= n then            //if space
  begin
   acount := acount + n;
   if acount = 32 then
    begin
     acount := 0;
     director[dirPtr] := accu;
     inc(dirPtr);
     accu := 0;
    end;
  end
  else                         //if no space
   begin
    director[dirPtr] := accu;
    accu := 0;
    inc(dirPtr);
    accu := w shr space;
    acount := n - space;
   end;
end;
Reading of n bits from the director: 
function readcode(n : byte) : dword;
//read n bits from director table
var mask : dword;
    space : byte;
begin
 if acount= 0 then
  begin
   accu := director[dirPtr];
   inc(dirPtr);
  end;
 mask := (1 shl n) -1;
 space := 32 - acount;
 result := accu shr acount;
 acount := acount + n;
 if acount = 32 then acount := 0
  else if acount > 32 then
        begin
         accu := director[dirPtr];
         inc(dirPtr);
         dec(acount,32);
         result := (result or (accu shl space));
        end;
 result := result and mask;
end;
After loading a new bitmap from disc, bm has to be converted to the 12 bit color format: 
function fixRGB12(c : byte) : byte; //helper of  colorfix12
//round 4 bit to $1f,$2f.....$ff
var c1 :  word;
begin
 c1 := (c + $8) and $1f0;
 if c1 < $20 then c1 := $20;
 dec(c1);
 result := c1 and $ff;
end;

procedure colorfix12;
//reduce colors in map to 12 bit
var x,y : word;
    Pline,p  : dword;
    color : dword;
    r,g,b : word;
begin
 clearCC;  //clear colorcount array
 for y := 0 to map.Height-1 do
  begin
   Pline := p0 - y*ps;
   for x := 0 to map.Width-1 do
    begin
     p := pline + (x shl 2);
     color := PDW(p)^;
     r := (color shr 16) and $ff;
     g := (color shr 8) and $ff;
     b := color and $ff;
     r := fixRGB12(r);
     g := fixRGB12(g);
     b := fixRGB12(b);
     color := b or (g shl 8) or (r shl 16);
     PDW(p)^ := color;
     setcolorbit(r,g,b);         //for colorcount;
    end;
  end;
 countcolors;
end;
For the complete Delphi project with the compression procedures, please contact me.
(david@davdata.nl)

Instructions

The spic program does not include help information.
The buttons speak for itself.
Pressing the unpack (decompress) button automatically causes comparison of the result with the original bitmap.

Statistics

During the compression process several counts are updated.
They are shown on the form:
    left copies from left neighbour
    exp.leftcompressed copies from left neighbour (exp = expanded)
    top copies from top neighbour
    exp.topcompressed copies from top neighbour (exp = expanded)
    stackcopies from stack
    new number of times a new color was inserted
The total count equals the pixelcount.

Size

The size of a bitmap is not tested.
Constant maxDir is the number of possible entries in the director.
Presently it is set to 250000.
So if compressing at 25%, pictures as large as 4 megabytes may be handled.
The paintbox on Form1 for showing the bitmaps is 800 pixels wide and 600 pixels high.