Answers of compasses / ruler constructions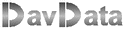

1.

Given is a line l and a point P, not on l.
Construct reflexion of P in l (call this point P').
Only use compasses.

Choose points A and B on l (distance not too small)
Draw arc around A, radius AP. Draw arc around B, radius BP.
P' is the intersection of the arcs.

Triangles APB and AP'B are congruent. (equal edges)
So LPAB = LP'AB
So, triangles PAS and P'AS are congruent (edge-angle-edge)
So, PS = SP' and PP' is perpendicular to l.

2.

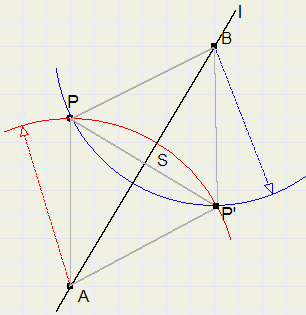
Given is a circle.
Construct the center.

Choose points A, B and C on the circle (distance not too small).
Draw lines AB and BC.
Construct perpendicular bisector lines of AB and BC.
Center M is the intersection of the bisectors.

Points on the perpendicular bisector of AB have equal distances to A and B.
Points on the perpendicular bisector of BC have equal distances to B and C.
M has equal distances to A, B and C.

3.

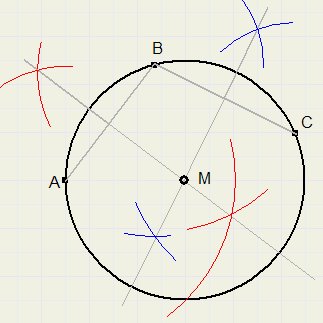
Construct an angle of 75 degrees.

75 = (180 - 30) / 2
Draw line l with points A and B.
Draw arc around B, radius AB. Call intersection with l C.
Draw arc around C, radius AB. Call intersection of arcs P.
LPAC = 30 degrees.
Construct bisector of large angle ( 150 degrees) between l and AP

LA₁ = 30 degrees because it's arc of 60 degrees.
LA₂₃ = 180 - 30 = 150 degrees.
LA₂ = LA₃ = 75 degrees.

4.

Multiply an angle by two.

Given is LA₁.
Draw circle around A, call intersections with edges P and S.
Draw arc around S, radius PS, intersection with circle (A) is T.
LTAP = 2 * LA₁

Triangles ABT and ABP are congruent (edge-angle-edge).

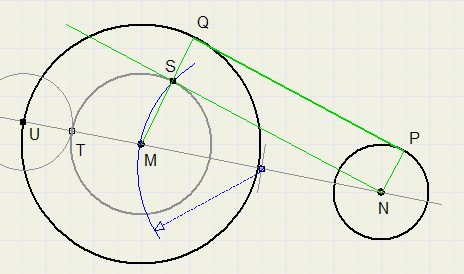
5.

Given are two circles and their centers M and N.
Construct a line that is the tangent of both circles.

Draw line through M and N ,
intersection with biggest circle is U.
Adjust compasses to radius of small circle and draw arc
around U, intersection with line is T.
Draw circle around M, radius MT.
Regard MN as diameter of circle.
Draw this circle.
Intersection with previous cicle is S.
NS is tangent of circle M.
Extend line MS, intersection with circle is Q.
Construct rectangle SNPQ.
PQ is the tangent of both circles.

SQ = NP = radius of circle N.
MQ and NP are perpendicular to PQ

6.

Construct an equilateral triangle given it's perimeter.

Start with linepiece PQ.
Draw temporary line through P and measure 3 equal distances from P.
Last point is T.
Draw TQ and parallel lines.
A and B are intersections of parallel lines with PQ.
Draw arcs around A and B, radius AB.
Intersection of arcs is C.
Draw triangle ABC.

PQ is divided in 3 equal parts.
PA = AB = BQ.
AC = BC = AB

7.

Construct a triangle ABC if given:
a. base AB, LA and the sum AC + BC

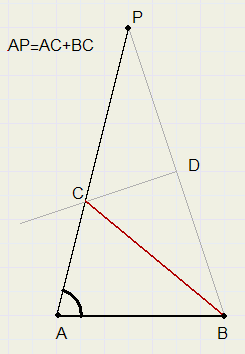
Given are AB and AP=AC+BC and LA
Draw line BP.
Construct perpendicular bisector of BP.
intersection of line with AP is C
In triangle ABC is AC + BC = AP

Triangles PDC and BDC are congruent (edge-angle-edge), so BC=PC

b. base AB, LA and the difference AC - BC

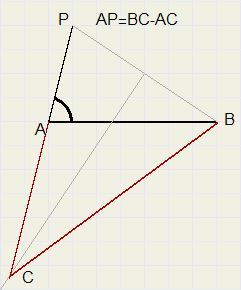
Draw line BP.
Construct perpendicular bisector of BP.
C is intersection of line with extension of AP.
ABC is the triangle.

C is on perpendicular bisector, so PC = BC.
AP = BC - AC

c. base angles A and B and the sum AC + BC

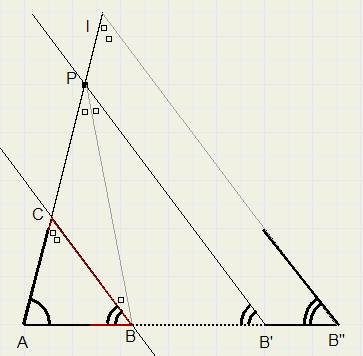
Draw angle A and (temporary) angle B'' on line AB''.
AP is given distance AC + BC.
Shift angle B'' along AB'', until P is on edge.
Call shifted point B'' B'.
Construct bisector of LAPB', B is intersection with line AB'.
Draw line trough B and parallel to B'P, intersection with AP is C.
ABC is the triangle.

See figure, any marked angle has (180 -LA - LB)/2 degrees.
Triangle BCP is isosceles, so BC = PC

d. base AB and distances from A (AD) and B (BE) to opposite edges.

Construct center M of AB and draw circle around M, radius MA.
Draw arc around A, radius AD.
Draw arc around B, radius BE.
D and E are intersections with circle M.
Draw lines through A and E and also through B and D.
intersection is C.
ABC is the triangle.

LAEB = LADB = 90 degrees, because AB is diameter.

8.

Divide a linepiece in parts having ratio 2 : 3

AB is the linepiece.
Draw temporary line through A and mark 2 equal distances (point V).
Extend AV and mark 3 more of the same distances (to point W).
Draw line WB and parallel line through V.
P on AB is the requested point. Trek lijn

Parallel lines divide intersecting lines in parts having the same ratio.

9.

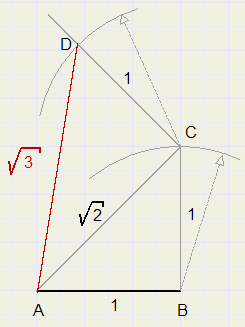
Construct a linepiece with length root(3) if a linepiece with length 1 is given.

AB = 1 (given).
Construct line perpendicular to AB, through B.
Draw arc around B, radius AB, C is intersection with line.
Construct line perpendicular to AC, through C.
Draw arc around C, radius AB, D is intersection with line.
AD is requested linepiece.

Apply pythagoras lemma in triangles ABC and ACD.

10.

Construct a right-angled triangle ABC (LC = 90 degrees) if given:

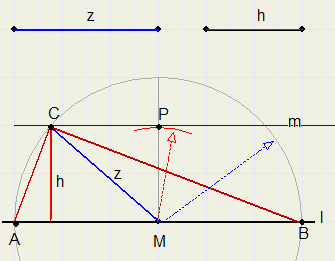
a. The distance from C to opposite edge and the length of the median from C.

Linepiece z is the median and h is the distance of C to AB.
Draw line l with point M.
Draw arc around M, radius is z.
Construct line perpendicular to l and through M.
Measure distance h on line from M (MP = h).
Construct line m through P and parallel to l.
intersection of m and circle is C.
ABC is the triangle.

LC holds is opposite diameter AB so LC = 90 degrees.
z is radius of circle through A,B and C.

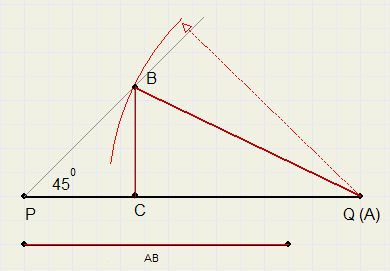
b. the hypothenusa AB and the sum AC + BC

PQ = AC + BC.
Construct angle of 45 degrees at P.
Draw arc around Q, radius AB, intersection with edge of LP is B.
Construct line perpendicular to PQ and through B.
Intersection with PQ is C
Call Q = A.
ABC is the requested triangle.

BC = PC, so BC + AC = PQ.

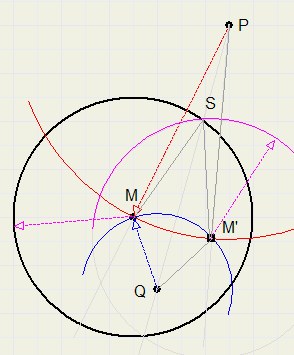
11.

Only use compasses in this exercise.
Use result of exercise 1.

Given are a circle en it's center M,
a point P outside- and a point Q inside the circle.
Construct the intersection of line l through P and Q with the circle.

Draw circle around P, radius PM.
Draw circle around Q, radius QM.
Intersection of circles is M' (M'is reflection of M in l)
Draw circle around M', radius is same as original circle M.
Intersection of circles is S.
S is the intersection of PQ and circle M.

PQ is perpendicular bisector of MM'.
MS = M'S, so S is on perpendicular bisector of PQ.

12.

Construct rhombus ABCD if given:
Angle A ( < 90 degrees) and the sum AC + BD of the diagonals..

Given are lines l and m and their intersection A.
Construct bisector of angle A and measure distance AP.
(AP = BD + AC, the diagonals sum)
Construct center M of AP.
Construct angle of 45 degrees at M.
(LAMD = 45 degrees)
Edge of this angle intersects l in point D.
Construct line through D, perpendicular to AP.
line intersects m in B.
Draw line parallel to AD and through B,
intersection with AP is C.
Draw CD.
ABCD is the requested rhombus.

The diagonals of a rhombus are bisectors of the angles and are perpendicular.
AS + SD = AS + SM = AM = PA /2.
AS + SD = (AC + BD) / 2 .