Square Roots: iterative and recursive procedures

download root program
download Delphi-7 project

Introduction

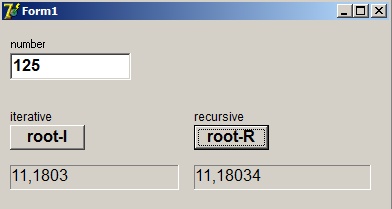
This article describes programs to calculate the square root of a number.
The programming language is Delphi.
Click on the lightning icon at the top to download the program or the complete project.
Two methods are used:
    1. iterative
    2. recursive
Iterative procedures are repeated many times.
In general such a program looks like this:



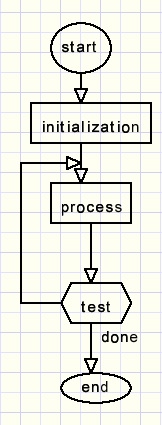
Initialisation means setting variables to an initial value and also resetting
a counter that controls the number of repetitions.

Recursive methodes call themselve.
Such methods look like this:



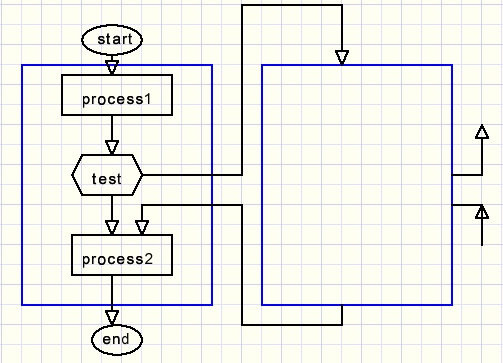
Process1 is executed, then a test follows to call the same procedure again.
After this test process2 follows.
Above, the same procedure is pictured twice just for understanding.
Local variables and parameters are placed on the stack so they are unique for each call.
Recursive procedures are very compact but harder to understand than iterative ones.

Iterative square root calculation

The number is a 32 bit positive integer (range 0..4294967295) which we call N (number).
The root is calculated in variable R (root) and other registers are A (accumulator)
and S (subtractor), the value that decrements A.



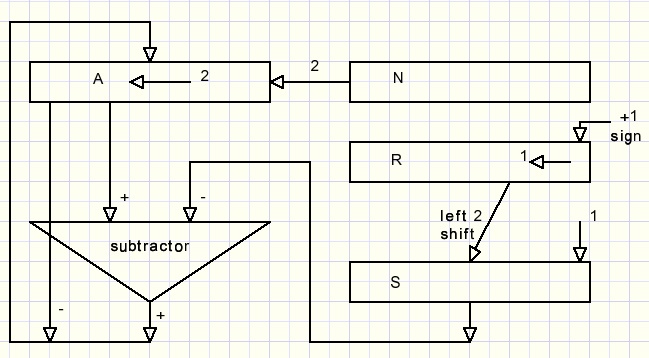
These are the steps of this algorithm:
    1. register N is the original number.
    2. A and R are set to zero.
    3. R is shifted 2 bits left and 1 is added, this value is saved in S.
    4. Registers A,N shift 2 bits left as 1 register.
    5. R shifts 1 bit left.
    6. Obtain the sign of A - S.
    7. if positive: A = A - S, set bit -0- of R to "1".
    8. repeat steps 3..7 (32 times).
After 16x two bits shifts left, register N equals zero.
The process continues with 16 more steps, producing bits behind the decimal point.
R now contains an integer value in bits 31..16 (then decimal point) followed by
bits 15..0 behind the decimal point.
A special procedure showRoot takes care of the display of the answer.

Theory

Say we calculate the root of a binary number and a partial answer is a.
Now we are looking for the next bit b, which can be 0 or 1.
The new answer is [ab]bits = 2a+b and it's square is (2a+b)2 = 4a2+4ab+b2.
The 4a2 vlue was previously subracted from the number which leaves a remainder N - a2.
So we have to find b in the expression 4ab + b2 = b(4a + b) so
for b being "1" S = (a shl 2) + 1 must be smaller then the remainder.
This changes the value of R and also the remainder and the process repeats to find the next b bit.
Note: in decimal arithmetic we have to subtract the highest square (0,1,4,9,..81) initially.
Binary arithemetic does not need that step because R = 0 automatically makes S = 1.

This is the iterative procedure:
(variables A,N,S are declared outside the procedure to be used also by the recursive method) 
var A,N,S : dword;
.....
procedure TForm1.Button1Click(Sender: TObject);
//calculate root, iterative way
var i : byte;
    R : dword; //result register, point in center
begin
 try
  N := strtoint(edit1.Text);
 except
  N := 1;
  edit1.Text := '1';
 end;  
 R := 0;
 A := 0;    //accumulator
 for i := 1 to 32 do       //root process
  begin
   A := (A shl 2) or (N shr 30);
   N := N shl 2;
   S := (R shl 2) or 1;    //subtract value
   R := R shl 1;
   if S <= A then begin
                   A := A - S;
                   R := R or 1;
                  end;
  end;
 showroot(R);
end;
procedure showRoot shows the result in a statictext component.
This result is split into an integer part and a fraction part behind the decimal point.
The fraction part is repeatedly multiplied by 10 which causes the decimal digits to pop up
left of the decimal point.
While multiplying the fraction, 5 is added for rounding purposes.
Accuracy is 4 digits.
Please see the source code for more details.

Recursive square root calculation

First some theory.
From algebra we know the factorization: a2-b2 = (a-b)(a+b).
So also:



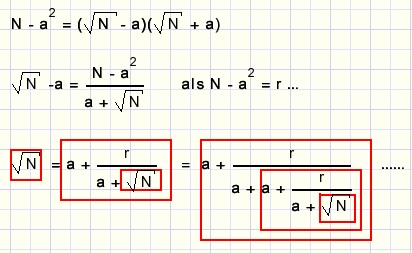
The recursion is clearly visible.
N is the original number.
a is the biggest number which square fits N.
r is the difference N - a2.
These values remain constant during the root calculation.
The deeper we descent in the denominators the smaller their impact,
so with each additional step the approximation gets better.

First a and r must be calculated before the recursive process may start.
The result appears in variable root. 
procedure TForm1.Button2Click(Sender: TObject);
//calculate root recursive way
var i,c  : byte;
    root : double;
begin
 try
  N := strtoint(edit1.text);
 except
  N := 1;
  edit1.Text := '1';
 end;
 c := 0;      //shift count
 if N > 0 then
  begin
   for i := 0 to 31 do                   //find highest -1- bit
    if ((1 shl i) and N) <> 0 then c := i;
   c := c shr 1;                         //root
   A := 1 shl c;                         //largest single bit root
   S := N - (A shl c);                   //S - A*A
   root := RecROOT(10);                  //depth = 10
  end
  else root := 0;
 statictext2.Caption := FormatFloat('#0.0#####',root);
end;
Here is the recursive function: 
function RecROOT(i : byte) : double;
//recursive root, i is depth
begin
 if i >1 then result := A + S/(A + RecROOT(i-1))
  else result := A + S/(2*A);
end;
The sole parameter is depth to end the recursion.
The function result is the square root of N.
Higher depths yield more accurate results.

See the source code for details.
To finish this explanation see below a picture of the Delphi-7 project at work: