a rolling circle problem

A rolling circle problem

Download program

Download Delphi project

Recently I received this problem:

I suggest, before reading further, that the reader tries to answer this question for himself.

Theory

We may stretch the perimeter of circle B and roll circle A over this straight line.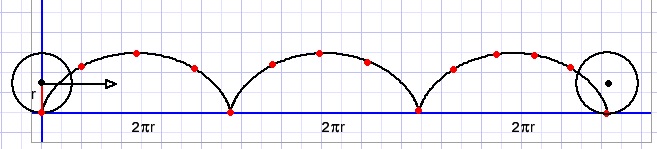

We notice three revolutions.
For those interested in the math:

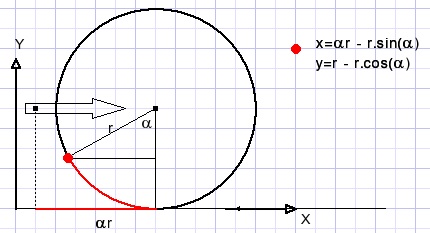
Movement of the red dot is given by a parametric function :
x and y are both expressed as a function of rotation angle α.
However, is this still true when circle A rolls over circle B?
Surprising answer: it is not.
See the geometry below:

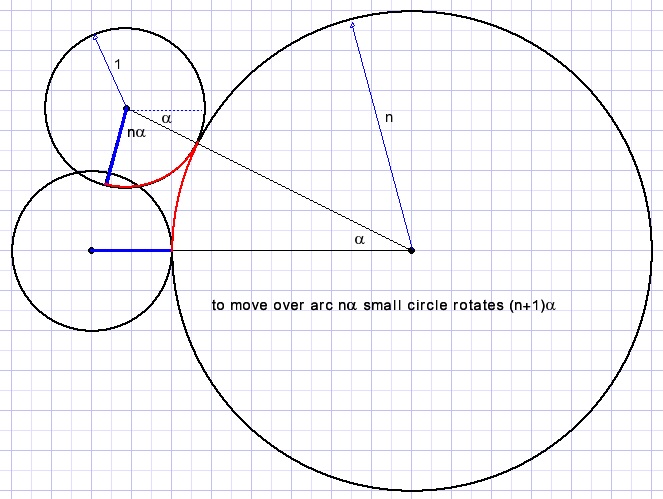
Circle A needs four revolutions to roll completely over circle B, not three as in the case of a straight line.
To illustrate this phenomenon I have written a small Delphi program.
The program adds some options

The theory for the case where A is the inner circle is left to the reader.

Program

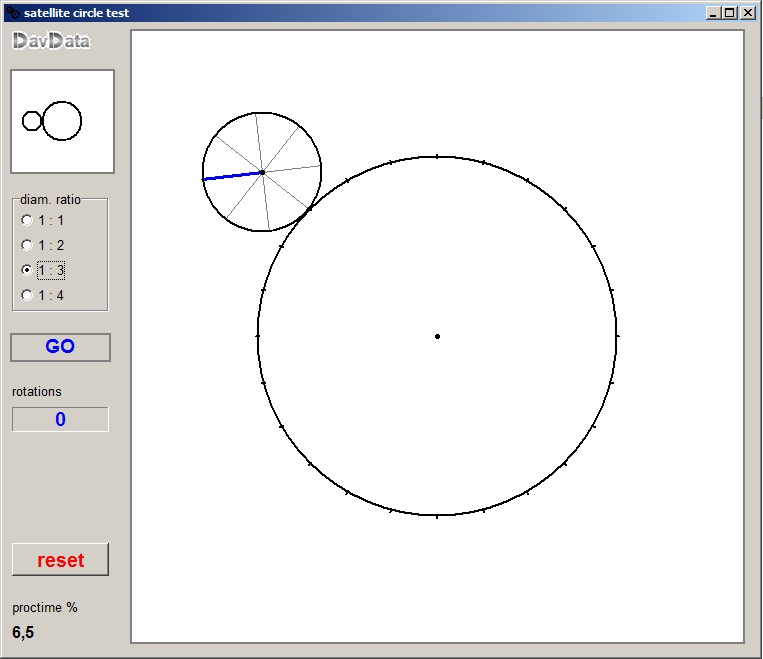
Select the diameter ratio.
Click on the left top image to select A as outer or inner circle.
Press GO to roll circle A over circle B.

Program description

The drawing is made in bitmap map.
Map is copied to paintbox1 on the main form to become visible.
The picture is repainted 100 times per second.
Left bottom label shows the percentage of processor time needed for an update.
See 2nd picture before.
Angle α starts from 0 and is incremented in steps of 0.005 radians.
A complete revolution takes 2π/0.005 = 1250 steps.
At 100 increments per second revolution time is 12.5 seconds.
Painting a complete new image takes:

Constants and variables

type Tmode = (modeIn,modeOut);
     Tradius = record
                rad1 : word;   //radius of circle B
                rad2 : word;   //radius of circle A
                xamp  : byte;  //rotation angle magnifier (=4 if ratio is 1:3)
               end;

Const pi2 = 2*pi;
      pi04 = pi/4;
      radOut : array[0..3] of Tradius =         //outer circle mode radius
               ((rad1:100 ;rad2:100 ;xamp:2),   //1:1
                (rad1:150 ;rad2: 75 ;xamp:3 ),  //1:2
                (rad1:180 ;rad2: 60 ;xamp:4 ),  //1:3
                (rad1:200 ;rad2: 50 ;xamp:5));  //1:4
      radIn  : array[0..3] of Tradius =         //inner circle mode radius    
               ((rad1:300 ;rad2:300 ;xamp:0),
                (rad1:300 ;rad2:150 ;xamp:1),
                (rad1:300 ;rad2:100 ;xamp:2),
                (rad1:300 ;rad2: 75 ;xamp:3));
var map : Tbitmap;
    cx,cy : word;     //center of circle B, measured in pixels
    sx,sy : word;     //center of circle A (satellite)
    radius1,radius2 : word; //radius of circles B and A, preset from constants array
    angle : double;   //rotation angle of circle A center around B center
    amp : byte;       //rotating angle magnifier, preset from constants array  
    GOflag : boolean; //control rolling 
    mode : Tmode = modeOut; //out- or inside circle A
    ModeEntered : boolean;  //for mode button enter / leave control  
    frotation : double;     //circle A rotation in floating point format
    rotations : byte;       //number of rotations of circle A

Procedure GOproc controls the rolling process

procedure GOproc;
var t1,t2 : Int64;
begin
 repeat
  t1 := getCPUticks;  //start CPU time
  paintmap;           //repaint image and copy to paintbox1
  t2 := getCPUticks;  //stop CPU time
  form1.proctimelabel.caption := formatfloat('0.#',proctime(t2-t1)*0.01);//% of 10msec.
  repeat
   application.processmessages;  //GOflag may be cleared by GObutton release
   t2 := getCPUticks;
  until proctime(t2-t1) > 10000;  //wait for 10 milliseconds since t1
  if angle >= pi2 then angle := angle - pi2;
  angle := angle + 0.005;
  incRotation(0.005);            //rotation increment for small circle A
  GOflag := GOflag and (angle <= pi2);   
 until GOflag = false;
end;

Note: GObutton actually is a TLabel.
It looks like a button by drawing a rectangle around it on the form canvas.
OnEnter, OnLeave, OnMouseDown and OnmouseUp events change the button edges.

I do not list here the procedures that paint the circles.
Please refer to the source code for details.

Conclusion

The problem answers (see first picture) are incomplete.
Answer (F) -none of the above- or (F) 4 is missing.
This once was question 17 of a SAT (Scholastic Aptitude Test) for high school students.
Only very few students noted the error.

I doubt that the teachers who formulated this question were aware of their mistake.