rivercrossing

Rivercross problems

Downloads:

rivercross1 program

rivercross2 program

rivercross1 source listing

rivercross2 source liesting

rivercross1 Delphi-7 project

rivercross2 Delphi-7 project

Introduction

This article describes two very similar puzzles and their solution by means of Delphi programs.
The two projects are called rivercross1 and rivercross2.
Both are well known problems.
(1) Is the problem of a farmer which has to row a cabbage, a goat and a wolf to the other bank of the river.
The boat only allows to carry one item at the time.
The farmer may not leave the goat and cabbage unattended: the goat would eat the cabbage.
Also the wolf and the goat may not be left unattended, for obvious reasons.

(2) Is the jealous husbands problem.
Three couples have to cross a river.
The boat has space for 2 people only.
Both husbands and wifes may row the boat.
Problem is that the jealous husbands do not tolerate that their wife is in company of another man
when they are at an opposite bank, even not when the other mans wife is present.

Focus is on the search algorithm. No efforts are taken to draw nice graphics.
Results are simply presented as a list. Items are indicated by characters.
Below first follows a description of the riverside1 program.
This problem is rather simple.

The riverside2 problem is more difficult however the program is very similar.
Only the differences with rivercross1 will be explained.

Rivercross 1

Programming is writing procedures and functions that operate on data structures.
What data is needed?
The items to move are the farmer (F) which rows the boat, the cabbage (C), the goat (G) and the wolf (W).
Their position is at the left- or the right bank of the river.
So, we need one bit per item 0: left bank 1: right bank.
To switch banks (row to opposite bank) requires the logical operation xor 1
Variable situation holds the 4 bits that indicate the place of each item:

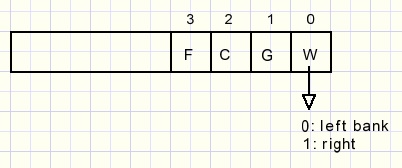
There are 4 items so situations range from 0 to 15 {(1 shl 4) - 1}

When moving between banks, the boat may be occupied by

ActionCode[0..4] array holds (binary) values

We have to remember which actions were taken.
The crossList[1..20] array holds action numbers 0..4.

Variable crossNr is the pass of the boat: 1,2,3....
Odd passes are from the left to the right bank, even passes are returns.
There is no need to have a special variable holding the boat direction.

Now, some situations are illegal, such as 0000 0110 meaning that the
goat and the cabbage are together and unattended at the right bank.
Procedure generateLegals fills a boolean array called legal
For each situation the array supplies true or false.

During the process no items disappear so the danger is real that items are moved
back and forth endlessly.
To prevent this we have to remember previously encountered situations.
Again there is a boolean array history[0..15] with a flag for each situation:
false if not encountered, true if the situation did occur during a previous move.

The solution of this puzzle simply is the list of actions (1..4) in array crossList[ ].
CrossList actually serves as a counter.
Note:
do not be confused by the terms action and actioncode.
action counts 1,2,3,4,1,2,3,4,... and actioncode[action] supplies the value to be xored
with the situation.
Initially the contents of crossList is (0 0 0 0 0 0 0 0 0 0 0...) indicating that no action took place yet.
crossNr = 0. situation = 0.
If the farmer and the goat move right : crossNr = 1 and crossList[ ] = (1 0 0 0 0 0 ....) .
Now situation = 0000 0000 xor 0000 1010 = 0000 1010.
When the farmer returns:
crossNr = 2; situation = 0000 1010 xor 0000 1000 = 0000 0010
crossList[ ] = (1,4,0,0...).
The puzzle is solved when situation 15 (binary 1111) is met : all items on the right bank.

Each action must be tested before because

function crossOK(ac,nr : byte) : boolean;
returns true if action ac for pass nr is allowed.
See the source code for details. There is very little code involved.

Now the core of this project: the search for a solution.
This is done by
function FindSolution(cs : TcrossStatus) : TCrossStatus;
where the crossStatus is csEND (no solution) or csSolution.
Below is the flowchart.
Looking at the source code may be shocking for programming purists:
it uses labels and goto statements.
The reason is crossing loops. Using repeat or while controlled loops would need extra
boolean variables making the code harder to understand.
If you can make readable code without the goto statements please let me know.

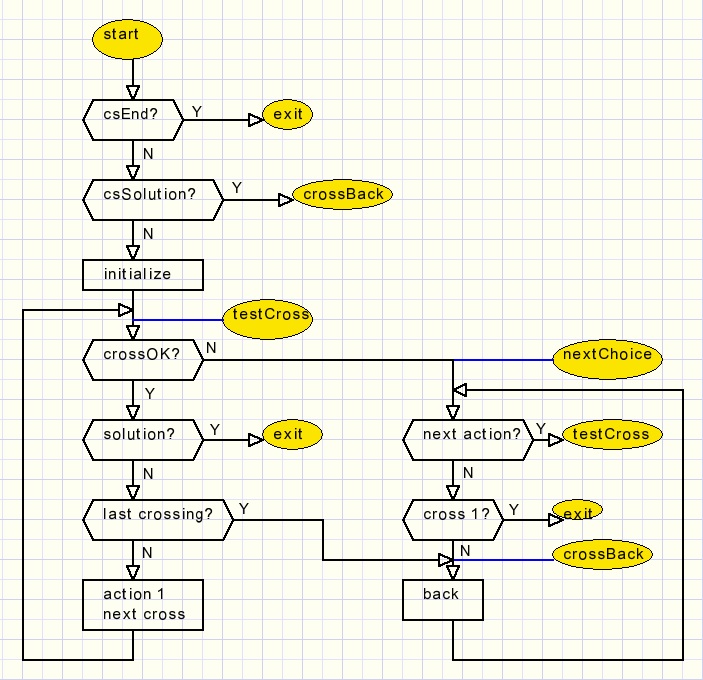
Please refer to the flowchart above for some details.
The function is called with csStart, csSolution or csEnd.
In case of csEnd the function exits immediately: there are no more solutions.
In case of csSolution the search goes for more solutions.
A jump is made to "crossBack".
With csStart, the search for a fresh solution begins.
Initialization:

 crossNr := 1;
 ac := 1;

If this pass is OK, the cross is registered:

 crossList[crossNr] := ac;
 situation := situation xor actionCode[ac];
 history[situation] := true;

Test for a solution

  if situation = maxSit then
  begin
   result := csSolution;
   exit;
  end;

Note: maxsit = 15, binary 1111, the maximum situation.

If no solution a test is made for the maximal pass reached:

  if crossNr = maxCross then goto crossBack;

If more passes are allowed

  inc(crossNr);
  ac := 1;
  goto testCross;

The next pass is selected and the ac counter is reset to 1.

If an action is tested false for some reason, the next action is tried: (label nextchoice)

 nextChoice:
  if ac < maxActionCode then
  begin
   inc(ac);
   goto  testCross;
  end;

If all actions were tried, the pass has to be taken back.
However, if we are forced to take back pass 1, this means there is no solution.

  if crossNr = 1 then
  begin
   result := csEnd;
   exit;
  end;

If not pass 1, the last pass must be removed:

 history[situation] := false;
 situation := situation xor actionCode[crossList[crossNr]];
 crossList[crossNr] := 0;
 dec(crossNr);

This takes us back at the previous pass.

Now we enter code at the label crossBack
This pass was not successful so we have to take it back and try the next action:

 crossBack:
  history[situation] := false;
  ac := crossList[crossNr];
  situation := situation xor actionCode[ac];
  crossList[crossNr] := 0;
  goto nextChoice;

Next some notes at the function crossOK which tests trial actions.
First test is whether the items are at the proper side of the river:

 code := actioncode[ac];
 pos := situation and code;                    //test items on proper bank
 if (nr and 1) = 1 then result :=  (pos = 0)   //nr is pass number (odd,even)
  else result := (pos = code);

For a pass from left to right bank, all items must be 0.
For a return path they must be 1.

Next test is for an illegal situation:

 newsituation := situation xor code;
 if result then
  result := legal[newsituation];

Last test is a check if this new situation occurred before:

 if result then result := (history[newsituation] = false);//avoid repetition

Below a reduced picture of the program + solution:

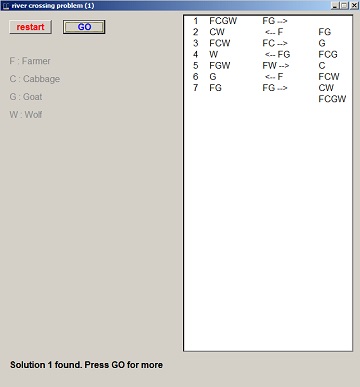
So far for rivercross1.

Rivercross2

The differences with rivercross1 are:

items:

The couples are named Aa (A male, a female) Bb and Cc.
So there are 64 situations: 0 to 63, binary 000000 to 111111

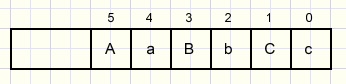
procedure generateLegals sets the legal array entry to true or false.
See the source code for the details.
procedure generateActionCodes fills the actionCode array and updates maxAction,
the number of actions.
The boat holds one or two people and combinations of husband and wife of different couples is not allowed.
First all 2 people actions are added to the actionList, then all single person actions.
Please refer to the source code for details.

Below a reduced picture of the program + solution:

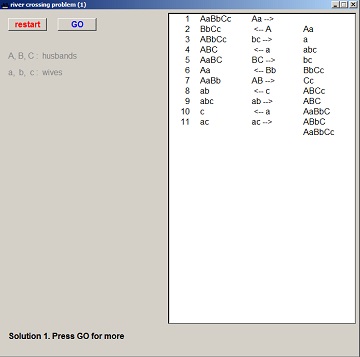
This concludes the riverside project descriptions.