

| About regular polygons |
Introduction
Below are pictured some (3 to 8 edged) regular polygons:
A regular N angled polygon may be considered as N identical isosceles triangles
which top angle equals 360/N degrees.
This Delphi project originated from a geometric problem.
Asked is to find the value of angle x in the picture below:
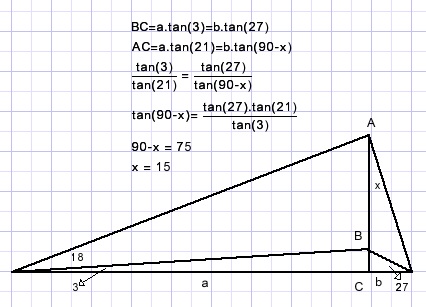
The algebraic solution presented here needs a pocket calculator.
In plane geometry problems are solved by the application of theorems and analytic reasoning.
A geometrical solution however is difficult until we realize that all angles
are multiples of three.
Angles of 3 degrees on a circle perimeter span arcs of 6 degrees of the circle
according to the theorem of Thales (Greek mathematician, 500BC).
Painting the triangle in the circumscribed circle of a 60 angled regular polygon shows
the answer right away: (polygon edges not painted)
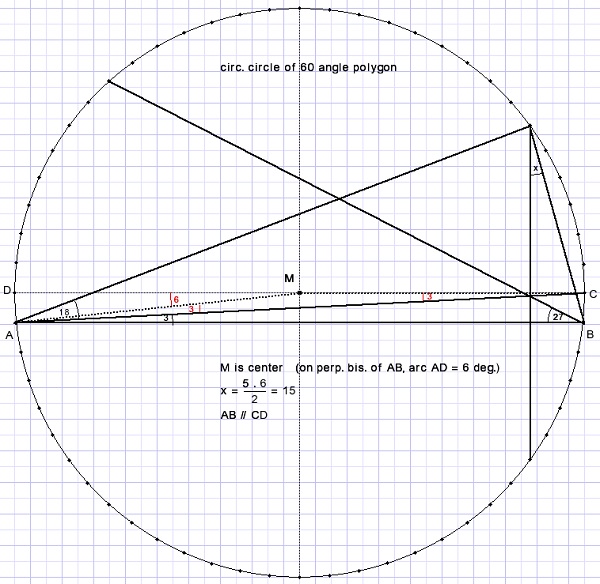
Each arc between points corresponds to 360/60 = 6 degrees.
X spans 5*6 degrees so x = 30/2 = 15 degrees.
In many other cases also this approach has been useful.
So I decided to build a project to investigate regular polygons.
Intermezzo (1)
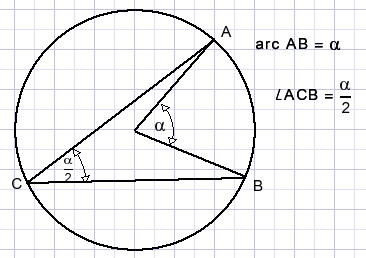
Angles may be measured as circle arcs.In the picture below, arc AB is expressed as angle α at the circle center.
The theorem of Thales states that an angle (such as C below) on a circle perimeter is half the arc (AB) it spans.
The proof is not presented here.
The project
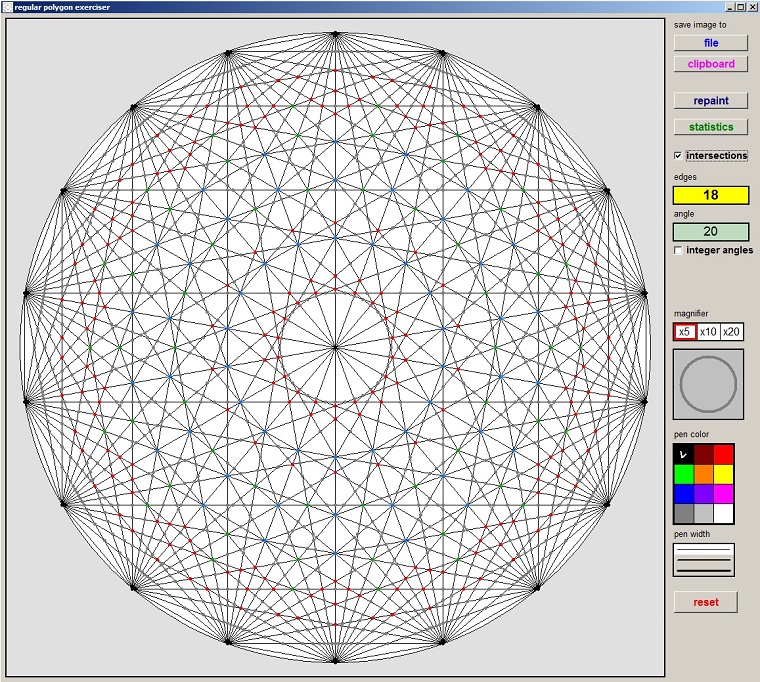
Below is a reduced picture of the project showing an 18 edged polygonwith its diagonals and the circumscribed circle.
Colored dots are painted at the intersection of diagonals.
Their color indicate the number of diagonals crossing.
Buttons allow for
-
- Saving the image to a file or to the clipboard
- Selecting the number of edges (3 to 60)
- Showing statistics about intersecting diagonals
- Coloring an intersection according to the number of diagonals crossing
- Drawing lines with selected color and pen width
- Shifting a magnifying glass over the image to clearly observe the intersection of diagonals
and also the operation of the magnifying glass.
Added to that the readers high school math may be refreshed.
Edge selection
A TLabel component is used as a button. TLabel has OnEnter and OnLeave events,allowing background color change on action.
procedure TForm1.Label1MouseEnter(Sender: TObject); begin label1.Color := $00c0ff; end; procedure TForm1.Label1MouseLeave(Sender: TObject); begin label1.color := $00ffff; end;A left mouseDown event on the "edges" label increases the number of edges,
a right mouseDown event decreases.
To do the job a timer is started which runs as long as the button is pressed.
This avoids clicking the button many times.
Checkbox2.checked causes the edgecount to be limited to integer arcs.
function IncEdges : boolean; //increment edgecount
var E : byte;
begin
if edgecount = maxEdge then result := false
else
begin
E := edgecount+1;
if form1.CheckBox2.checked then
while (E < maxEdge) and (360 mod E > 0) do inc(E);
setEdgecount(E);
result := true;
end;
end;
procedure setEdgeCount(newcount : byte);
const ff = '0.##';
begin
edgecount := newCount;
arc := 2*pi/edgecount;
tanArc := tan(arc); //values needed later
with form1 do
begin
label1.Caption := inttostr(edgecount);//show edgecount
label3.Caption := formatfloat(ff,360/edgecount);//show arc
end;
end;
Intermezzo (2)
Traditionally, angles are measured in degrees where 360 degrees indicate a full circle turnaround.Reason for 360 is that this number has many divisors.
The calculation of sine and cosine ratios is done by polynomials where the angle is expressed in radians.
360 degrees equals 2 x π radians, which is the perimeter of a circle with a radius of 1.
Note that the constant π always is an approximation. There does not exist a number or fraction which is exactly π.
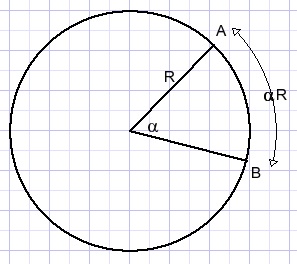
An angle of α radians at the center of a circle with radius R spans an arc (AB) of length αR.
Calculating the polygon
Painting is done in a 1001 * 1001 pixels bitmap.An odd number, so pixel[500,500] is the exact center.
The circumscribed circle has [500,500] as center, its radius is 480 pixels.
After painting, the bitmap is made visible by copying it to paintbox1 on form1.
A bitmap has coordinates [0,0] at the left top.
In the case of painting we need the exact and absolute position of a pixel which is relative to the left top.
These points however are rounded floating point values.
Calculating intersections of diagonals requires precision, so floating point variables have to be used for the coordinates.
Calculations become more simple regarding center pixel [500,500] as origin [0,0].
Here we use both methods.
The edges of the polygon are stored in the Alist array: { Alist[1] is the top, angles 2,3,.. run clockwise}
The Alist array both holds integer and floating point values for the polygon edge positions.
The floating point values are relative to the center [500,500].
Const maxEdge = 60;
type TCpoint = record
x,y : word; //absolute pixel position
rx,ry : single; //real value relative to screen center
end;
var Alist : array[1..maxEdge] of TCpoint;//list of polygon angles
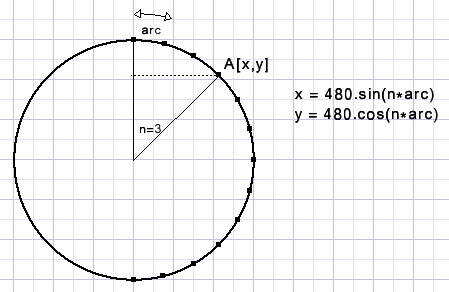
procedure Arc2XY(var x,y : single; a : byte);//a= 1,2….
//supply x,y coordinates of polygon angle
var na : single;
begin
na := arc*(a-1);
x := 480*sin(na);
y := 480*cos(na);
end;
Filling the Alist[ ] array:
var i : byte;
x,y : word;
rx,ry : single;
begin
for i := 1 to edgecount do
begin
arc2XY(rx,ry,i);
Alist[i].x := round(rx)+500;
Alist[i].y := 500-round(ry);
Alist[i].rx := rx;
Alist[i].ry := ry;//UP + DOWN - ; center relative
end;
Please refer to the source code for painting of the edges and diagonals.
Two identical bitmaps are used:
-
Map1 holds the polygon, diagonals and circle.
Map2 is a copy of map1 and adds intersection points and also holds lines during drawing.
modified parts of map2 are erased by copying part of map1 to map2.
Modified parts of map2 are copied to paintbox1 to become visible.
This technique avoids erasing the paintbox which would cause flickering.
Intermezzo (3)
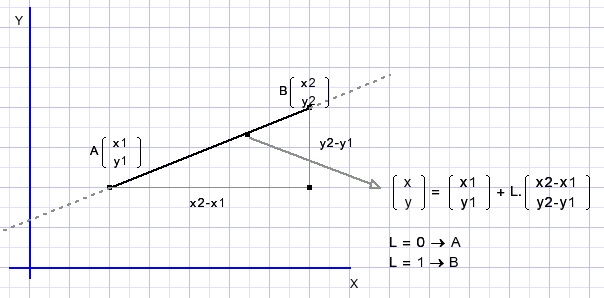
The calculation of intersections is done with vector calculus.Below is shown the vector equation of a line (AB):
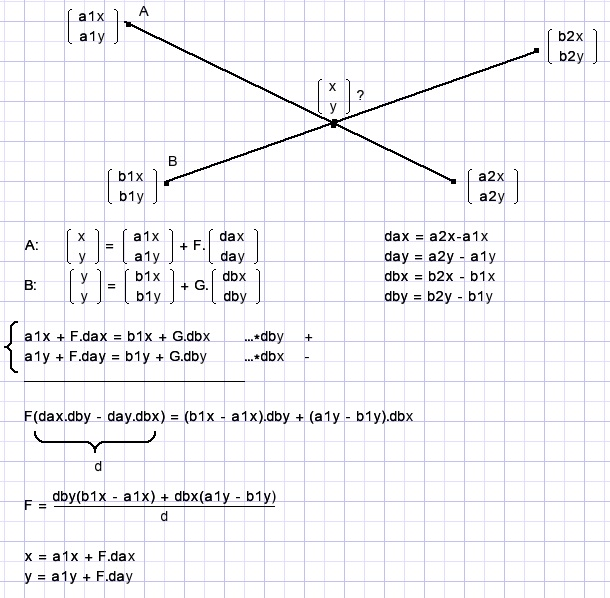
Variable naming (such as a1x):
//1 : begin of line, 2: end of line
//a :line through point A. b : through point B
To find the intersection point of two lines:
Program
function GetIntersection(var x,y : single; a1,a2,b1,b2 : byte) : boolean; //return intersection of diagonal a1-a2 and b1-b2 ; a1,2 b1,2 = 1,2,3…Alist index //Return "false" in case of parallel lines (d = 0)Saving time
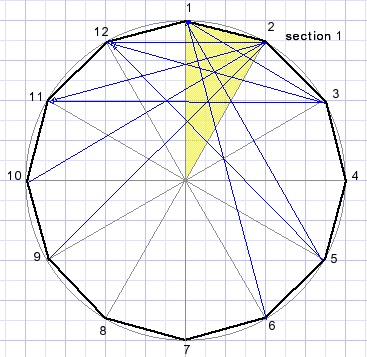
An n- angled polygon has n(n-1)/2 lines (edges plus all diagonals).
A regular 60 angled polygon counts 1710 diagonals.
To investigate intersections would require the examination of 1,461,195 line pairs.
However, polygons have rotation symmetry.
All sections are the same. Only the diagonals that cross section 1 have to be examined.
Once knowing these intersection points the similar points in other sections may be calculated by rotation.
const INSTlistmax := 10000;
type TIntersection = record
count : byte;
x,y : single;
end;
var INTSlist : array[1..INTSlistmax] of TIntersection;//list of intersections in section 1
Intersection points are added to above INTSlist.In case the (x,y) coordinates are already in the list , count is incremented.
Intermezzo (4)
Rotation of points.A point A(x,y) is regarded the addition of its x and y coordinates.
X and Y are rotated separately, then the results are added.
Rotation is clockwise.
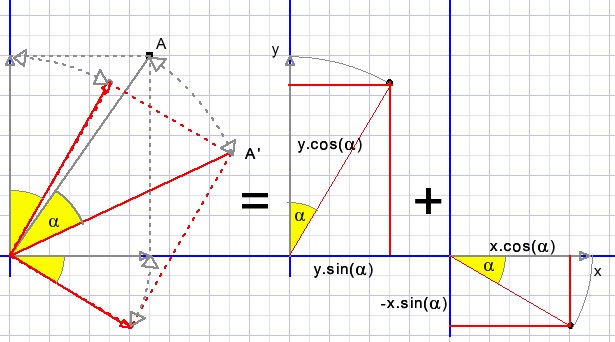
α is the rotation angle.
X becomes x.cos(α) and also decreases y by x.sin(α)
Y becomes y.cos(α) and increases x by y.sin(α)
Added together:
A(x,y) becomes A'(x',y').
X becomes x'= x.cos(α) + y.sin(α)
Y becomes y'= y.cos(α) - x.sin(α)
Procedure :
function GetDotColor(c : byte) : dword;
begin
case c of
2 : result := $808080; //grey
3 : result := $0000ff; //red
4 : result := $00b000; //dark green
5 : result := $ff8000; //blue
6 : result := $ffff00; //light blue
7 : result := $00c0ff; //orange
8 : result := $ff00ff; //purple
else result := $00000000; //black
end;//case
end;
procedure paintIntersections(sx,sy : single; count : byte);
//paint intersection point (sx,sy) of chords in all segments
//count : number of intersecting lines per point
var r : Trect;
x,y : word;
i : byte;
a,sina,cosa,rx,ry : single;
clr : dword;
begin
clr := getDotColor(count);
with map2.Canvas do
begin
pen.Color := clr;
brush.color := clr;
brush.Style := bsSolid;
for i := 0 to edgecount - 1 do
begin
a := i*unit1.arc;//not arc procedure but variable
sina := sin(a);
cosa := cos(a);
rx := sx*cosa + sy*sina;
ry := sy*cosa - sx*sina;
x := round(rx)+500;
y := 500-round(ry);
r := rect(x-2,y-2,x+3,y+3);
ellipse(r);
form1.PaintBox1.Canvas.CopyRect(r,map2.canvas,r);
end;//with
end;//for
end;
The magnifying glass
The magnifying glass shows its portion of the screen 2, 5 or 10 times enlarged.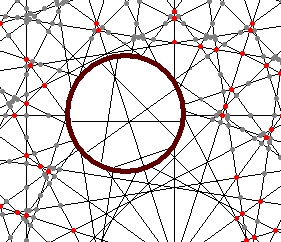
This is obtained by multiplying all coordinates by m (2,5,10) while calculating possible intersections
with the magnifying glass circle.
There is no actual enlargement of the picture at all, lines are recalculated.
The magnifying glass radius is 55 pixels. To simplify calculations,
all coordinates are shifted to make the magnifying glass center the origin [0,0] of the coordinate system.
After calculations off course the coordinates are shifted back in place.
Picture below shows the calculation of the intersection of a line and a circle.
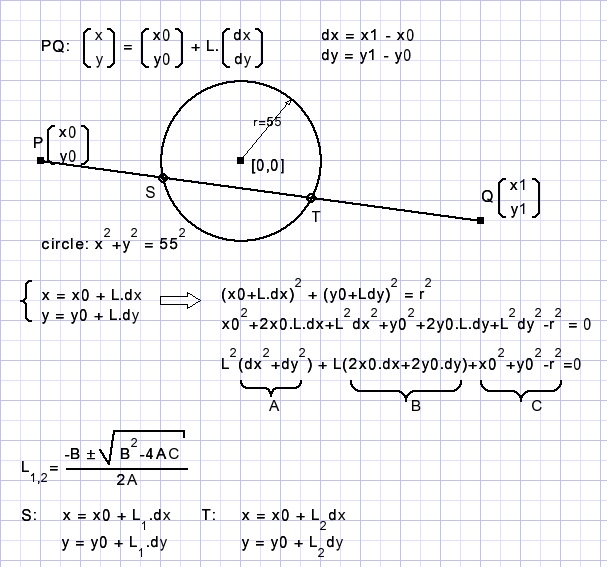
The result is line ST.
While moving, the magnifying glass center is [magX,magY] which are absolute pixel coordinates.
Before calculations:
Xoffset = (magX-500)*m
Yoffset =(magY-500)*m
Coordinate adjustment (angle [i]):
X0 = m*Alist[i].rx - Xoffset
Y0 = m*Alist[i].ry - Yoffset
Now origin [0,0] is at the center of the magnifying glass.
For all diagonals a check is made for intersection with the glass.
If the root is negative in above calculations there is no intersection.
See procedure paintmagnifierglass; for details.
Keep in mind that the real rx,ry values in Alist[ ] are relative to paintbox center [500,500].
Of course there is more to say. Such as the conditions for 3,4,…diagonals intersecting at one point,
which must be based on symmetry.
But these considerations I save for other times.
To use the magnifying glass, select the magnification,
click on the glass which places it at the paintbox center.
Shift the glass by placing the mousepointer over the glass, press mouse button and move mouse.
To remove the magnifying glass, click again on the button.
When the glass is not selected lines may be drawn by mouse movement.
This may be useful in solving geometry puzzles which was the reason for this small project.
Using floating point arithmetic
Floating point values that are a power of 2 (such as 0.5 , 0.25) are exact values.0.1 or π are approximations.
Calculations using these values increase inaccuracy.
In this project 32 bit "single" floating point variables are used.
Their accuracy is 6 to 7 (decimal) digits.
Example:
Var a,b : single; Begin .... If a = b then ....//this condition will probably never be "true" // Instead this works If abs(a-b) < 1e-6 then ....// a almost equal to bSo at all times the programmer has to realize the amount of inaccuracy.

