

 |
 |
download RANKS |
Ranks |  |
 |
Introduction
Ranks is a program that assigns a sequential number (rank) to a combination, permutation or partition.Given a rank, the combination permutation or partition may be generated.
Given a combination permutation or partition, the rank may be calculated.
Ranks is freeware and may be copied without restriction.
Installation
Click on the download (lightning) icon at the top of this page to download ranksRanks ships as a single .exe file.
It contains In-Line help information.
The system is Windows 95 and up.
Minimum screen resolution is 600*800.
There is no installation procedure, just copy to a map of choice.
The Windows Registry is not changed.
The size is 268kB.
Combinations
A combination is a selection of elements from a set, where each element may be choosen onceand the sequence of selection is unimportant.
In this program (ranks) the elements are always the natural numbers 1,2,3,4,......
The maximum number of elements is 50.
The ranking of combinations may be usefull in the analyses of lotto games or any case where
combinations have to be generated in a systematical way.
The number of possible combinations of k elements from a set of n is written as
-
C(n,k) = n!/(k!*(n-k)!)
| rank | combination |
| 0 | 1-2 |
| 1 | 1-3 |
| 2 | 1-4 |
| 3 | 2-3 |
| 4 | 2-4 |
| 5 | 3-4 |
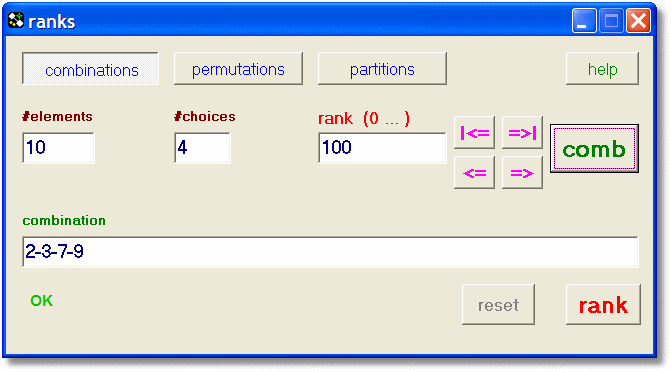 |
| 4 elements of 10: rank 100 |
Permutations
A permutation is a sequence of elements.Elements are always named 1,2,3,4,....
The maximum number of elements is 12.
n elements have n! permutations, where n! = n.(n-1).(n-2)........(3).(2).(1)
Ranking a permutation is usefull when sequences have to be generated in a systematical way,
as is the case in logigram puzzle solving.
Below are listed all permutations of a set of 4 elements
| rank | permutation |
| 0 | 1-2-3-4 |
| 1 | 1-2-4-3 |
| 2 | 1-3-2-4 |
| 3 | 1-3-4-2 |
| 4 | 1-4-2-3 |
| 5 | 1-4-3-2 |
| 6 | 2-1-3-4 |
| 7 | 2-1-4-3 |
| 8 | 2-3-1-4 |
| 9 | 2-3-4-1 |
| 10 | 2-4-1-3 |
| 11 | 2-4-3-1 |
| 12 | 3-1-2-4 |
| 13 | 3-1-4-2 |
| 14 | 3-2-1-4 |
| 15 | 3-2-4-1 |
| 16 | 3-4-1-2 |
| 17 | 3-4-2-1 |
| 18 | 4-1-2-3 |
| 19 | 4-1-3-2 |
| 20 | 4-2-1-3 |
| 21 | 4-2-3-1 |
| 22 | 4-3-1-2 |
| 23 | 4-3-2-1 |
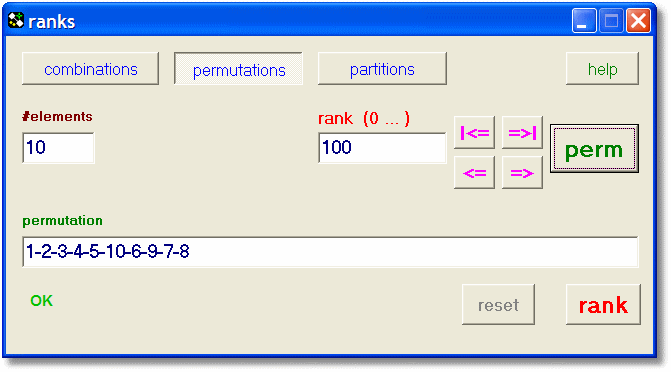 |
| permutation of 10 elements: rank 100 |
Partitions
A partition of a number n is a list of numbers which have a sum of n.The sequence of the numbers is not important so they are shown sorted.
The maximal number is 50.
Ranking a partition may be usefull in cases where partitions have to be generated in a
systematical way, which is needed in the analyses of certain Nim games.
Below are listed all partitions of the number 6, together with the ranks.
| rank | partition |
| 0 | 6 |
| 1 | 5-1 |
| 2 | 4-2 |
| 3 | 4-1-1 |
| 4 | 3-3 |
| 5 | 3-2-1 |
| 6 | 3-1-1-1 |
| 7 | 2-2-2 |
| 8 | 2-2-1-1 |
| 9 | 2-1-1-1-1 |
| 10 | 1-1-1-1-1-1 |
Number 6 has 11 partitions, ranked 0 to 10.
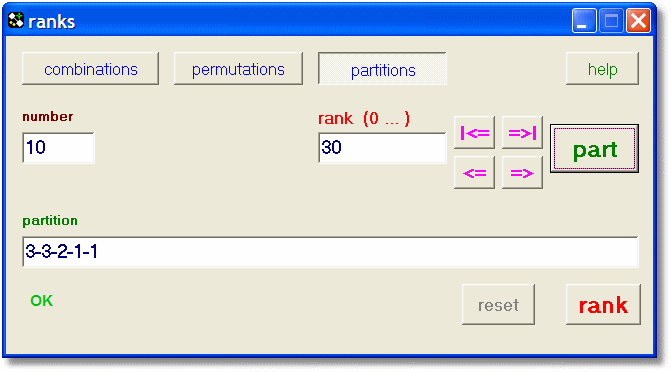 |
| number 10: partition number 30 |
How it works
Table below lists some type definitions and variables.
type Taction = (acComb,acPerm,acPart);
Taa = array[1..50] of byte;
var action : Taction = acComb;
elements : Taa;
partList : Taa; //make next partition until = elements
pmax : byte; //scratch for partitions
faculties : array[0..12] of longInt;
number : byte;
choices : byte;
rank : longInt;
maximum : boolean = false;
|
Rename "action" to avoid this conflict.
Note: faculties[n] is set to n! on creation of the form.
Note: elements[ ] holds the combination, permutation or partition.
number,choice and rank are the numeric values of edit components on the form.
Calculating the combination from a rank
function C(n,k : byte) : longInt;
//calculate combinations k of n
var i : byte;
tt,nn : double;
begin
if (k = 0) or (k = n) then
begin
result := 1; exit;
end;
//--
if 2*k > n then k := n - k;
tt := 1; nn := 1;
try
for i := 0 to k-1 do
begin
tt := tt * (n-i);
nn := nn * (k-i);
end;
result := trunc(tt/nn);
except
result := 0;
end;
end;
procedure newComb;
var r,comb : longInt;
i,n,k : byte;
elList : array[1..50] of byte;
endrepeat : boolean;
begin
if Checkelements then exit;
if checkChoices then exit;
if CheckRank then exit;
//----
r := rank;
k := 1;
if rank = C(number,choices)-1 then maximum := true
else maximum := false;
clearelements(elements);
for i := 1 to 50 do ElList[i] := i;
//----
for n := 1 to choices do
begin
endrepeat := false;
repeat
comb := C(number-k,choices-n);
if r >= comb then
begin
inc(k);
r := r - comb;
end
else endrepeat := true; ;
until endrepeat;
elements[n] := ElList[k];
inc(k);
end;//for n
//---
ShowElements(choices);
end;
|
Calculating the rank of a combination
procedure newCombRank;
//calulate rank from combination
var i,j,min : byte;
begin
if checkelements then exit;
if getCombination then exit;
if checkchoices then exit;
//--
for i := 1 to choices do
if (elements[i] = 0) or (elements[i] > number) then
begin
post(16);
exit;
end;
//--
for i := 1 to choices-1 do
if elements[i] = elements[i+1] then
begin
post(17);
exit;
end;
//--
min := 1;
rank := 0;
for i := 1 to choices do
begin
for j := min to elements[i]-1 do
rank := rank + C(number-j,choices-i);
min := elements[i]+1;
end;
//--
form1.edit4.text := inttostr(rank);
post(6);
end;
|
Calculating the permutatation of a rank
procedure newPerm;
//make permutation from number, rank
var i,k,x : byte;
r : longInt;
list : array[1..12] of byte;
begin
if CheckElements then exit;
if CheckRank then exit;
//-----
r := rank;
if rank = faculties[number]-1 then maximum := true
else maximum := false;
clearElements(elements);
for i := 1 to 12 do list[i] := i;
//--
for i := 1 to number do
begin
x := r div faculties[number-i] + 1;
r := r mod faculties[number-i];
elements[i] := list[x];
for k := x to 11 do list[k] := list[k+1];
end;
//--
ShowElements(number);
end;
|
Calculating the rank of a permutation
procedure newPermRank;
var i,j : byte;
list : array[1..12] of byte;
begin
if checkelements then exit;
if GetPermutation then exit;
//--
for i := 1 to 12 do list[i] := i;
rank := 0;
for i := 1 to number do
begin
j := 1;
while elements[i] <> list[j] do inc(j);
rank := rank + (j-1)*faculties[number-i];
for j := j to 11 do list[j] := list[j+1];
end;
form1.edit4.text := inttostr(rank);
post(6);
end;
|
Calculating the partition of a rank
procedure newPart;
var n : longInt;
max,min,acc : byte;
s : string;
begin
if CheckElements then exit;
if CheckRank then exit;
//--
clearElements(elements);
maximum := false;
elements[1] := number;
max := 1;
for n := 1 to rank do
begin
acc := 0;
while (max > 0) and (elements[max] = 1) do
begin
dec(max);
inc(acc);
end;
if elements[1] = 1 then
begin
maximum := true;
rank := n-1;
form1.edit4.text := inttostr(rank);
showElements(number);
exit;
end;
//-----
dec(elements[max]);
inc(acc);
min := elements[max];
while acc > 0 do
begin
inc(max);
if acc >= min then
begin
elements[max] := min;
acc := acc - min;
end
else
begin
elements[max] := acc;
acc := 0;
end;
end;//while
end;//for
ShowElements(max);
end;
|
Calculating the rank of a partition
procedure NextPartition;
//generate next partition in partlist
var n : longInt;
min,acc : byte;
s : string;
begin
acc := 0;
while (pmax > 0) and (partlist[pmax] = 1) do
begin
dec(pmax);
inc(acc);
end;
dec(partlist[pmax]);
inc(acc);
min := partlist[pmax];
while acc > 0 do
begin
inc(pmax);
if acc >= min then
begin
partlist[pmax] := min;
acc := acc - min;
end
else
begin
partlist[pmax] := acc;
acc := 0;
end;
end;//while
end;
procedure newPartRank;
var i,count,sum : byte;
begin
if GetPartition(count) then exit;
if checkelements then exit;
for i := 2 to 50 do partlist[i] := 0;
partlist[1] := number;
pmax := 1;
rank := 0;
//--
repeat
sum := 0;
for i := 1 to count do
if partlist[i] = elements[i] then inc(sum)
else break;
if sum <> count then
begin
inc(rank);
NextPartition;
end;
until sum = count;
form1.Edit4.text := inttostr(rank);
post(6);
end;
|
Partitions are generated sequentially, starting from (rank) 0.
The Delphi-7 project
Interested in the complete source code of the ranks project? Click [ here ] to download.

