pythagoras tree

Pythagoras Tree

This article describes the programming of a so called Pythagoras tree.
See picture below:

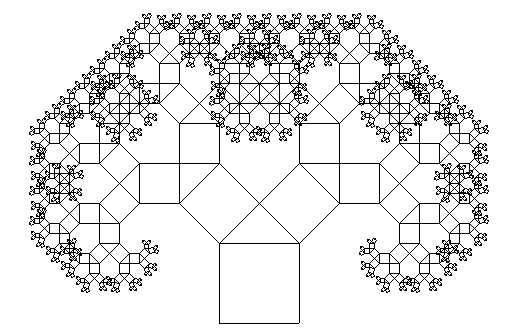
The program is recursive, it calls itself.
Programming language is Delphi.
The drawing was produced with one single procedure which is less then 30 lines of code in length.

Please look at the next picture:

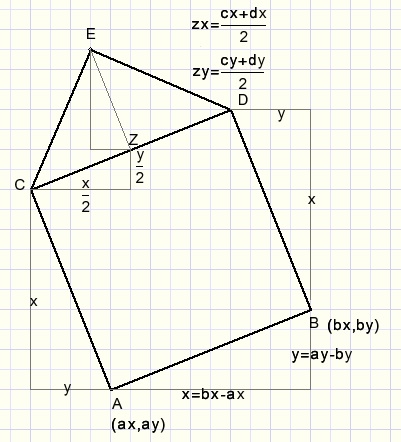
Starting point is the line AB.
procedure makeTree(...) is called with the ccordinates of points A and B.
This procedure calculates the coordinates of points C,D and E and draws lines
AC,BD,CE and DE.
After that the procedure calls itself twice:
1. with the coordinates of points C and E.
2. with the coordinates of points D and E.

A counter is needed to avoid endless repetition.
This counter is parameter depth in the procedure call.
makeTree decrements depth for each new call
and a call is made as long as depth is greater than 1.

This is the procedure:

procedure makeTree(ax,ay,bx,by : smallInt; depth : byte);
//paint part of tree
var cx,cy,dx,dy,ex,ey : smallInt;
    x,y,zx,zy : smallInt;
begin
 x := bx-ax;
 y := ay-by;
 cx := ax-y;
 cy := ay-x;
 dx := bx-y;
 dy := by-x;
 zx := (cx + dx) div 2;
 zy := (cy + dy) div 2;
 ex := zx - (y div 2);
 ey := zy - (x div 2);
 with form1.PaintBox1.Canvas do
  begin
   pen.color := $000000;
   pen.width := 1;
   moveto(ax,ay);
   lineto(cx,cy);
   lineto(dx,dy);
   lineto(bx,by);
   moveto(cx,cy);
   lineto(ex,ey);
   lineto(dx,dy);
   if depth > 1 then
    begin
     maketree(cx,cy,ex,ey,depth-1);
     maketree(ex,ey,dx,dy,depth-1);
    end;
  end;
end;

Notes:
1. In a computer screen the y coordinates positive direction is down.
2. The coordinates of point A are called (ax,ay) etcetera
3. The coordinates are variables of type smallInt with range -32768..32767
4. ABCD is a square.
5. LCED = 45⁰, CE = DE.
6. Point Z is an intermediate step to calculate point E.
7. The first call is makeTree(360,595,440,595,10).
8. Variables x,y,cx,cy...are local, exist on the stack, so are unique for each call.