a Prime Number Generator

Introduction

Prime numbers are numbers that are only divisible by 1 or by themself.
The first 10 prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.

A number can be factorized only in one unique way, so prime numbers
may be considered the building blocks of numbers.

Prime numbers play an important role in mathematics, specially when coding secret messages as is the case
in electronic banking.
This article describes how the program "prime200" calculates prime numbers.

Theory

The number investigated to be prime should be divided by all smaller primes.
The quotient may not be an integer, because this means that the number is a multiple of this other prime.
We also could say: the remainder of the integer division may not be zero.
In the Delphi programming language, the operator mod calculates the remainder of an integer divide.

The fomula P mod d yields the remainder of the division of P by d.
If this result equals zero, P is not a prime number.

We research the number 229 to be prime.
The sequential divisors may be d = 2, 3, 4, 5..................., 228 and when all remainders are unequal to zero
we know that P is prime.

However, the job may be accomplished with less work.
Prime numbers bigger than 2 cannot be even, because these numbers are multiples of 2.
So starting from 2 we may increase P and it's divisors by 2.
Divisor d than has the values : 3, 5, 7, 9, .......
But looking more closely at number above 5 we observe:
.......7, 11, 13, 17, 19, 23, 29, 31, ...............an increment by 2 never happens twice in a row.

Reason is that prime numbers above 6 have the form 6K+1 or 6K+5, where K = 1,2,3,4......
please look:
    - 6K may be divided by 6
    - 6K + 2 may be divided by 2
    - 6k + 3 may be divided by 3
    - 6K+4 may be divided by 2
so the list if divisors becomes (for prime numbers above 6 and with the form 6K+1 or 6K+5):
......5, 7, 11, 13, 17, 19, 23, 25, 29...............alternating addition of 2 or 4.

But another accelleration is possible.
Computers distinguish between real numbers and integers.
The operator for division of real numbers is '/ '.
For integer divides, the (Delphi language) operator is div.
These division neglects the digits right of the decimal point.
We continue investigation of number 229:
    1).........229 div 13 = 17..........and the next divisor is 17
    2).........229 div 17 = 13
In line 1) the quotient is bigger than the divisor (17 > 13)
In line 2) the quotient is smaller then the divisor.

This means that it is meaningless to increase the divisor again and keep dividing 229,
because if 229 had a (prime) factor we had met this factor allready.
Note, that if P = a.b where a and are prime, then
    P mod a = 0
    P mod b = 0
    P div a = b
    P div b = a.......this division is superfluous if a < b
As soon as (P div d) < d, we may stop the division of P.

Below is a flowchart of the Delphi procedure where the primes are calculated.
The procedure calculates the next 200 primes starting from P.

Flowchart

variables:
    P : the number to be investigated
    ip : increment value of P, alternating 2,4,2,4,...
    d : the divisor of P
    id : increment value of d, so alternating 2,4,2,4,.....
    n : the index of the prime number on the screen, 0..199
In this chart are
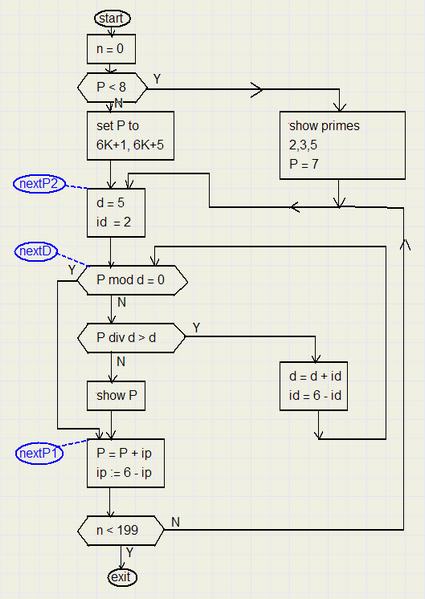
    rectanglesfunction-boxes: calculations are done here
    hexagondecision-boxes: a test is done
    a result of Y (yes) or N (no) forces execution of a different
    part of the program
    ellipseslabels: a place in the program to jump to

Program

Download the program by clicking on the lightning icon at the top of this page.
There is no installation procedure, just copy "prime200.exe" to a map of choice.

Interested in the complete Delphi-7 project with the source code? Click [here ]